从零开始写算法——二分-寻找旋转排序数组中的最小值
一、题目背景
给定一个升序数组,它被某个未知的下标旋转了,例如:
原始数组:[0,1,2,4,5,6,7]
旋转后:[4,5,6,7,0,1,2]
要求:找到旋转后的数组的最小值。
二、二分为什么可行?
很多同学第一眼看到这题会想:“这不是无序的吗?还能二分?”
其实,虽然整体无序,但它由两个递增子数组拼接而成:
[4,5,6,7] + [0,1,2]
这意味着——
我们依然可以通过一次比较排除掉一半的答案空间。
只要能做到这一点,二分搜索就可以用。
我们先来看下面这张图,这是把题目抽象后的图像:
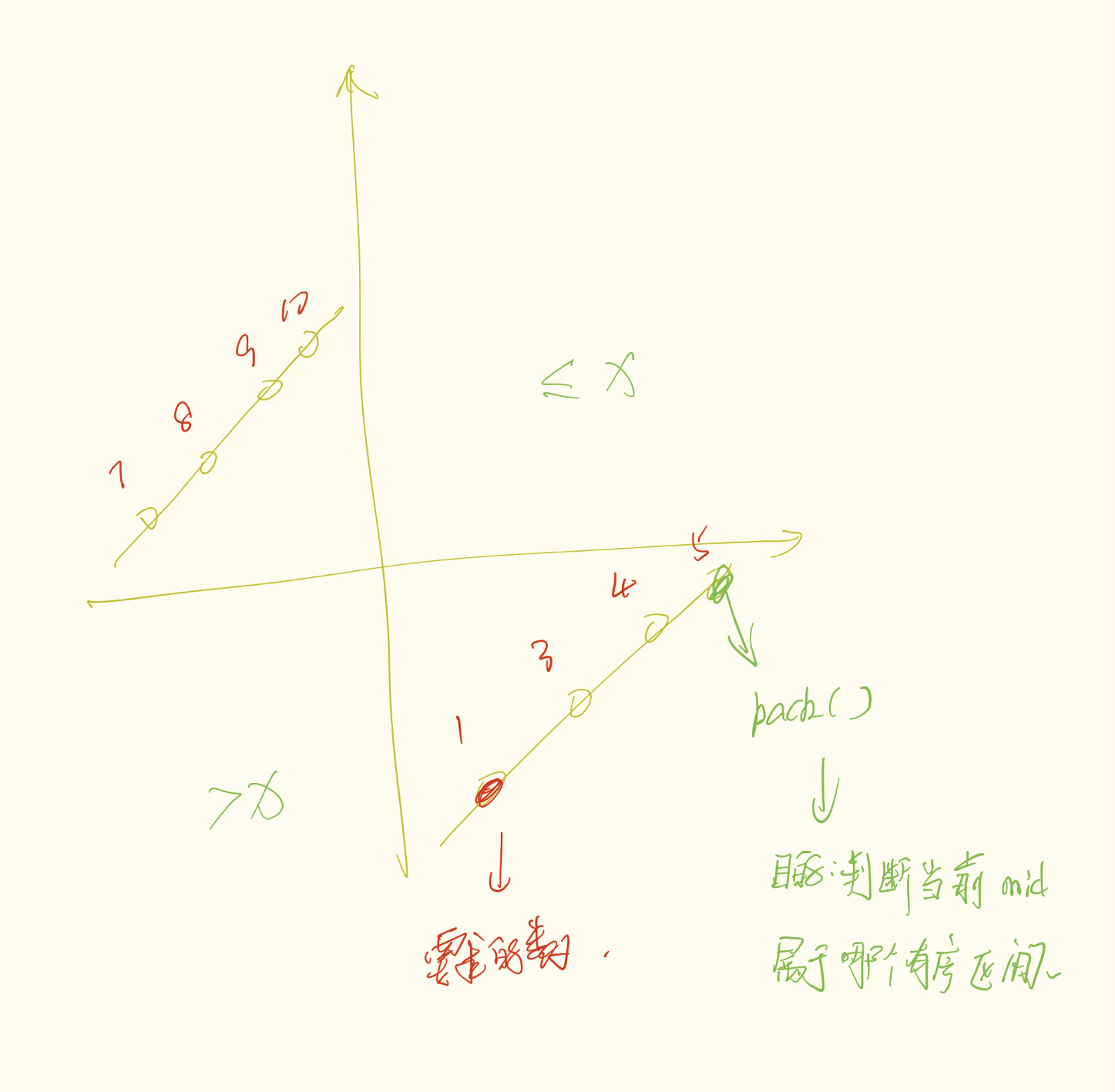
这里注意两个数一个是1,这是答案,一个是5,这个其实可以看作是x轴分界点(注意这里并不是x = 0,我们只是做一个抽象区分),其实就是大于5我们就放到左边(染红色),小于等于5就放右边(染蓝色),最后蓝色第一个数字就是答案。(注意:我们这个过程中并不关心每个序列真的值的增减性,我们只需要判断染色范围)
三、红蓝染色思路
我们可以把整个数组分成两种区域:
红色区域:所有
nums[i] > nums.back()的元素蓝色区域:所有
nums[i] <= nums.back()的元素
而我们要找的最小值,就是蓝色区域的第一个数。
举个例子:
nums = [4,5,6,7,0,1,2]
nums.back() = 2红蓝分布:
红色:[4,5,6,7]
蓝色:[0,1,2]
目标就是找到第一个蓝色元素的位置。
四、代码实现(查找型二分写法)
class Solution {
public:int findMin(vector<int>& nums) {// 思路: 我们说的二分要求有序,其实也可以从整体把控它的“部分有序性”。// 只要一次判断可以排除掉一半可能,就能用二分。// mid 与 back 比较:// 如果 nums[mid] > nums.back(),说明 mid 在红色区域,最小值在右侧;// 否则 mid 在蓝色区域,最小值可能在左侧(包括 mid 本身)。int left = 0;int right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] > nums.back()) {left = mid + 1; // mid 在红色区域,答案在右边} else {right = mid - 1; // mid 在蓝色区域,答案可能在左边}}return nums[left]; // 退出时 left 正好指向蓝色区域第一个}
};
五、循环逻辑详解
1️⃣ 判断条件
nums[mid] > nums.back()
→ 说明 mid 在红色区域,最小值一定在右侧,所以 left = mid + 1。
否则
→ mid 在蓝色区域,最小值可能是 mid 或更左边,所以 right = mid - 1。
2️⃣ 为什么可以返回 nums[left]?
当循环结束时(left > right),有两个事实成立:
right一定停在最后一个红色元素的位置left一定指向第一个蓝色元素(也就是最小值)
因此直接返回 nums[left] 就行。
如果你此时画一下红蓝区间,会发现:
红红红红蓝蓝蓝↑ ↑right left
循环结束后 left 恰好越过红区,落在蓝区第一个上。
六、调试理解
以 nums = [4,5,6,7,0,1,2] 为例,追踪过程:
| left | right | mid | nums[mid] | 比较结果 | 下一步 |
|---|---|---|---|---|---|
| 0 | 6 | 3 | 7 | 7 > 2 | left = 4 |
| 4 | 6 | 5 | 1 | 1 <= 2 | right = 4 |
| 4 | 4 | 4 | 0 | 0 <= 2 | right = 3 |
退出循环时:left = 4, right = 3,返回 nums[4] = 0 ✅
七、总结
| 关键点 | 含义 |
|---|---|
| 能否二分的核心 | 一次比较能排除一半可能性 |
| 红蓝划分标准 | nums[mid] > nums.back() |
| 答案所在区域 | 蓝色第一个元素 |
| 循环类型 | 查找型(<=) |
| 返回位置 | nums[left] |
八、延伸:红蓝染色法的通用套路
这种思路其实是通用的。
比如:
找第一个 ≥ target 的元素:蓝色 = “符合条件”
找最后一个 < target 的元素:红色 = “不符合条件”
只要能把区间“染色”,就能写出稳健的二分。
九、写在最后
这道题虽然只有几行代码,却几乎涵盖了二分的所有核心概念:
红蓝染色法
边界控制与不变量
<=与<循环的区别二分的本质:一次判断排除一半空间
当你真正理解这些逻辑后,
二分搜索就不再是“模板题”,而是一种思维方式。
