P10668 BZOJ2720 [Violet 5] 列队春游(自己加强版) 题解
P10668 BZOJ2720 [Violet 5] 列队春游
正整数数列 h1,h2,⋯,hnh_1,h_2,\cdots,h_nh1,h2,⋯,hn。设 ppp 为 1∼n1\sim n1∼n 的随机排列。
定义 hi′=hpih'_i=h_{p_i}hi′=hpi。定义 prei\mathrm{pre}_iprei 为最大的 j<ij\lt ij<i 满足 hj′≥hi′h'_j\ge h'_ihj′≥hi′(如果不存在,规定为 000)。
求出 ∑i=1n(i−prei)\displaystyle \sum_{i=1}^n (i-\mathrm{pre}_i)i=1∑n(i−prei) 的期望值,保留两位小数输出。1≤n≤3001\leq n\leq 3001≤n≤300,1≤hi≤10001\leq h_i\leq 10001≤hi≤1000。
和dp无关,只是期望。可以做到O(V) 。
我们看题目中要求 Σ(i−prei)\Sigma (i-pre_i)Σ(i−prei),考虑拆开算还是一起算,拆开算的话有点困难,因为要和排列之后所处的位置有关。所以我们一起算 。
转化一下题意,求 i−preii-pre_ii−prei,便要求 iii 左侧,紧贴着 iii 的小于 hih_ihi 的数有几个再加 111(加 111 是因为 i−preii-pre_ii−prei 是 iii 到 preipre_iprei 中间的数个数加 111)。也就是说,对于每一个紧贴着 iii 的,高度小于 hih_ihi 的,都会对 iii 有 111 的贡献。
考虑怎么解决这个问题(对于每一个紧贴着 iii 的,高度小于 hih_ihi 的,都会对 iii 有 111 的贡献),画图来说:
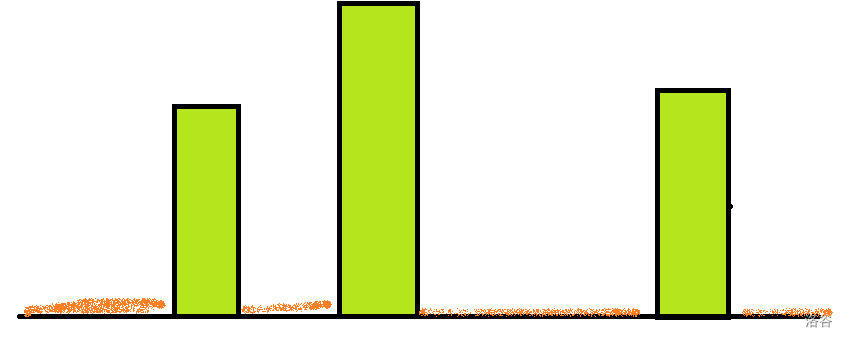
其中绿色的是大于等于 hih_ihi 的数,设我们有 sumisum_isumi 个等于 hih_ihi 的数,cnticnt_icnti 个小于 hih_ihi 的数,那么我们就有 n−cnti+1n-cnt_i+1n−cnti+1 个空。
我们先只考虑一个 hih_ihi,因为对于其他相同的 hih_ihi 答案是一样的。
小于它的数 ppp 会产生贡献,那 ppp 一定是 hih_ihi,在一个格子里的,概率为 n−cnti+1n-cnt_i+1n−cnti+1。又因为有 cnticnt_icnti 个小于它的,所以再乘 cnticnt_icnti。
(另一种理解方式: 那这个 hih_ihi 出现在每个空的概率为 1n−cnti+1\frac{1}{n-cnt_i+1}n−cnti+11,任意一个小于它的数的概率出现在每个空的概率同样为这个(我们令小于 hih_ihi 的数和 hih_ihi 一旦出现在同一个空里,就把小于它的数放在 hih_ihi 前面,因为这样才有贡献)。又因为一共有 n−cnti+1n-cnt_i+1n−cnti+1 个空,所以最终柿子为 (n−cnti+1)×(1n−cnti+1×cntin−cnti+1)(n-cnt_i+1)\times(\frac{1}{n-cnt_i+1}\times\frac{cnt_i}{n-cnt_i+1})(n−cnti+1)×(n−cnti+11×n−cnti+1cnti))。
化简一下为 cntin−cnti+1\frac{cnt_i}{n-cnt_i+1}n−cnti+1cnti。
又因为一共有 sumisum_isumi 个等于 hih_ihi的数,所以对于所有 hih_ihi 的答案为 cnti×sumin−cnti+1+sumi\frac{cnt_i\times sum_i}{n-cnt_i+1}+sum_in−cnti+1cnti×sumi+sumi ,为什么要加 sumisum_isumi 呢,因为前面讲的转化柿子会多一个 111,我们在这里加上。
整体来说,我们按照值域做,对于每个取值求一个这个柿子,再求和。复杂度为 O(V)O(V)O(V)。
code:
#include<bits/stdc++.h>
using namespace std;
const int N=2005;
int n,b[N];
int sum,mx;
double ans;
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){int x;scanf("%d",&x);++b[x];mx=max(mx,x);}for(int i=1;i<=mx;i++){ans+=1.0*sum*b[i]/(n-sum+1)+b[i];sum+=b[i];}printf("%.2lf",ans);return 0;
}
启示:
- 期望也可以按照值域啊这样的统计贡献。
- 可以考虑它给其他人带来的贡献,或者其他人给他的。
- 转化题意/拆柿子……
