当前位置： 首页 > news >正文

【C++】AVL 树

news 2025/11/14 10:05:57

目录

一. 概念

二. 实现

1. 插入

左单旋

右单旋

右左双旋

左右双旋

2. AVL 树的验证

三. 整体代码

一. 概念

控制树有多种方法，我们这里讲平衡因子（不是必须，也可以用其他方法实现 AVL树）

当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均 搜索长度

性质、判定：
        1. 它的左右子树都是AVL树
        2. 右子树高度 - 左子树高度（平衡因子）的绝对值不超过1(-1/0/1)

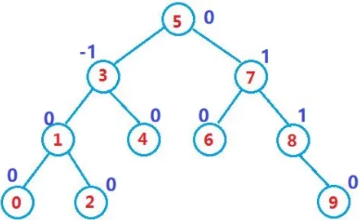增删查改：高度次 O(logN)

二. 实现

AVLTree.h

template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factor 平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){ }
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv) { }private:Node* _root = nullptr;
};

1. 插入

二叉搜索树的比对、插入

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;cur->_parent = parent;// 更新平衡因子、判断是否控制平衡// ...return true;
}

下面就要更新平衡因子、判断是否控制平衡（平衡因子本质是病，0 不用动，1 就要溯根，2 就得治）

1. 新增在左，parent 平衡因子 --
2. 新增在右，parent 平衡因子 ++
3. 更新后 parent 平衡因子 == 0，说明 parent 子树高度不变，不会再影响祖先，不用再继续沿着路径往上更新，直至 root（插入结束）
4. 更新后 parent 平衡因子 == 1 or -1，说明 parent 子树高度变化，会再影响祖先，但没有影响 AVL 树的大规则，继续沿着路径往上更新，直至 root（重复 12，再判断属于 3-6 的哪种情况）
5. 更新后 parent 平衡因子 == 2 or -2，说明 parent 子树高度变化且不平衡，要对 parent 子树旋转，让他平衡（插入结束）
6. 更新到根节点（插入结束）

旋转的时候要注意：
        1. 保持是搜索树
        2. 旋转后变成平衡树且降低这个子树的高度

bool Insert(const pair<K, V>& kv)
{// ... 插入节点// 更新平衡因子、判断是否控制平衡while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0) // 更新结束{break;}else if (parent->_bf == 1 || parent->_bf == -1) // 继续往上更新{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2) // 子树不平衡，需要旋转{if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent); // 单纯的右边高，左单旋}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent); // 单纯的左边高，右单旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent); // 右左双旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent); // 左右双旋}break;}else{assert(false);}}return true;
}void RotateL(Node* parent) { }

左单旋

巧记：右边高就要向左压，且是直线，左单旋
        旋转都是从头上绕过去，parent 把挨得近的 cur 的孩子节点叼走，自己当小弟，cur 当大哥

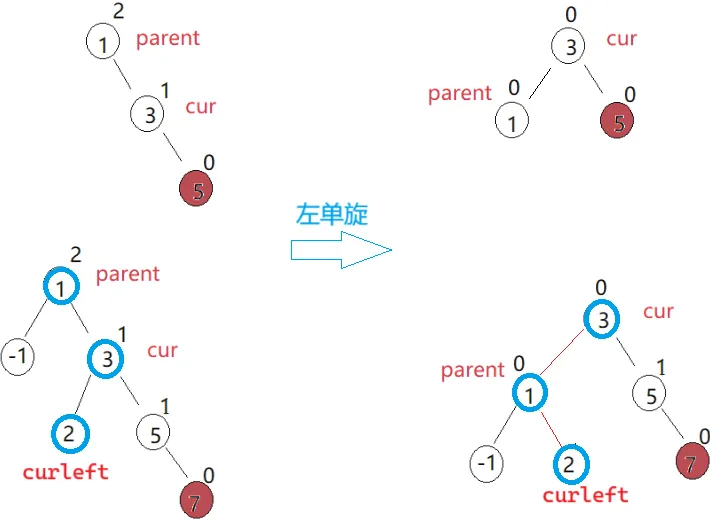
主要动了蓝圈 3 个节点，其他节点不变

核心操作：
parent->_right = cur->_left;
cur->_left = parent;

单有核心操作不够，此时 2 的父亲是 3；3 的父亲是 1；1 的父亲指向上面或是空

void RotateL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;// 2个核心步骤parent->_right = curleft;cur->_left = parent; if (curleft) // 调整curleft父亲节点的指向{curleft->_parent = parent;}parent->_parent = cur; // 调整parent父亲节点的指向//cur->_parent = ppnode; 错：ppnode还要和cur建立关系// 调整cur父亲节点的指向if (_root == parent){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = cur;elseppnode->_right = cur;cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;
}

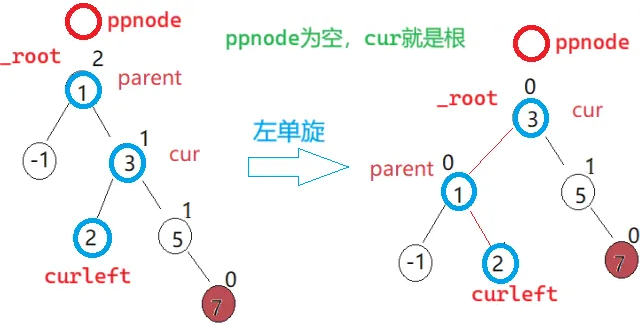
为什么 parent、cur 的平衡因子都要更新成 0？        看抽象图

插入之前，abc 是符合 AVL 规则的子树

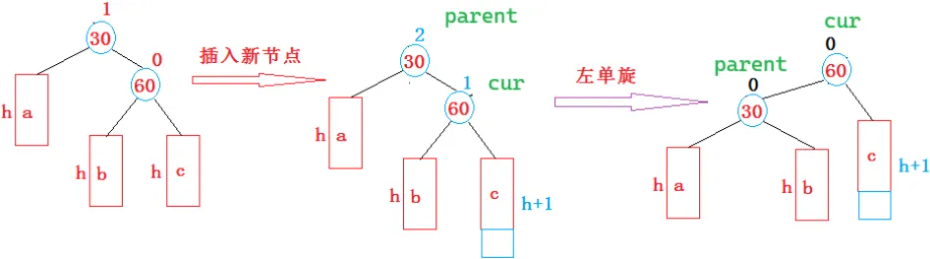
右单旋

巧记：左边高就要向右压，且是直线，右单旋
        旋转都是从头上绕过去，parent 把挨得近的 cur 的孩子节点叼走，自己当小弟，cur 当大哥

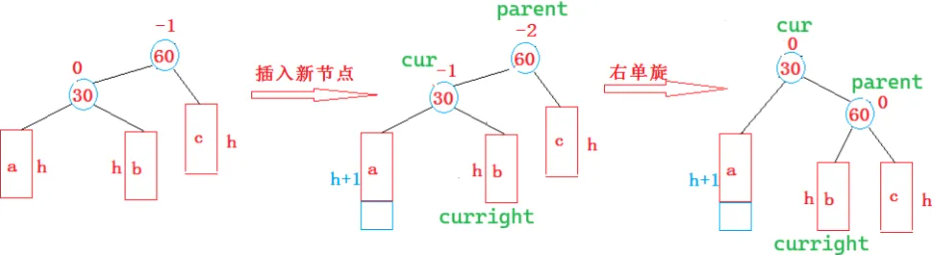
核心操作：
parent->_left = cur->_right;
cur->_right = parent;
void RotateR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;// 2个核心步骤parent->_left = curright;cur->_right = parent;parent->_parent = cur; // 调整parent父亲节点的指向if (curright) // 调整curright父亲节点的指向{curright->_parent = parent;}//cur->_parent = ppnode; 错：ppnode还要和cur建立关系// 调整cur父亲节点的指向if (_root == parent){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;
}

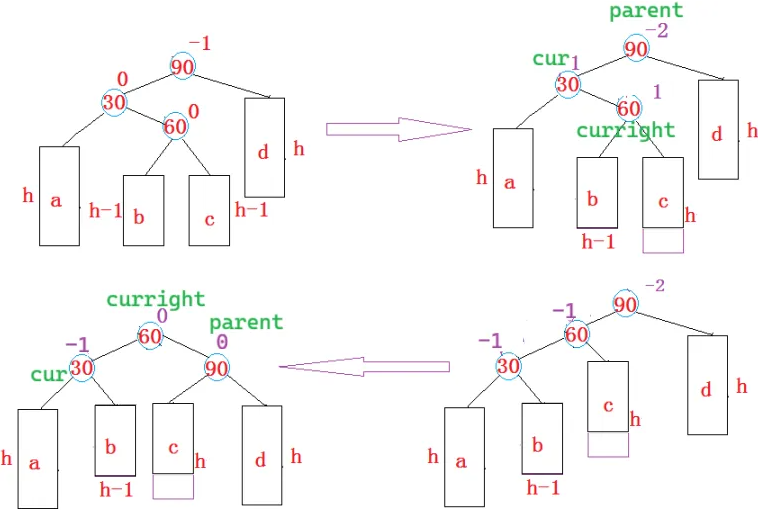
右左双旋

巧记：右边高就要向左压，本应左单旋，折线，就要先右单旋，再左单旋
        最下面的节点，把左右孩子给离它近的 cur、parent，自己当大哥

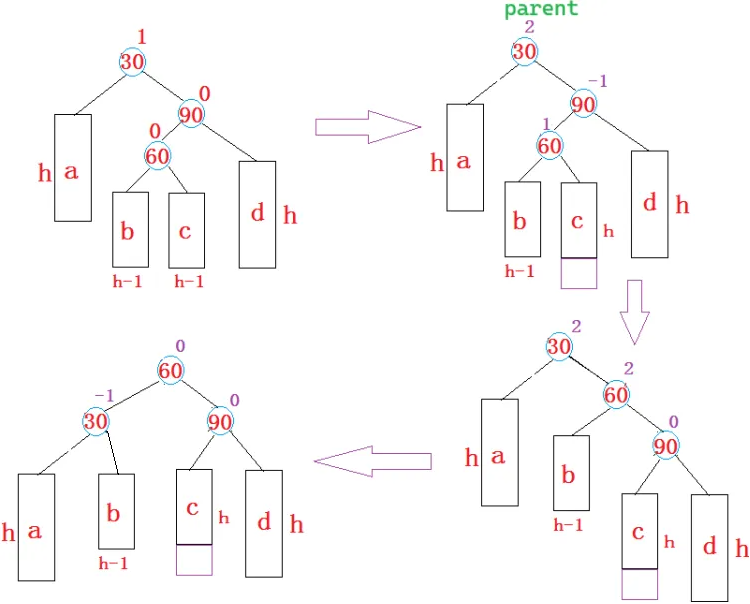
先以 90 为旋转点，右单旋；再以 30 为旋转点，左单旋

RotateR(parent->_right);
RotateL(parent);

平衡因子分析：

h == 0：60 就是新插入的节点

h > 0：

1. 插入到 c 诱发右左双旋（上面的图）
2. 插入到 b 诱发右左双旋

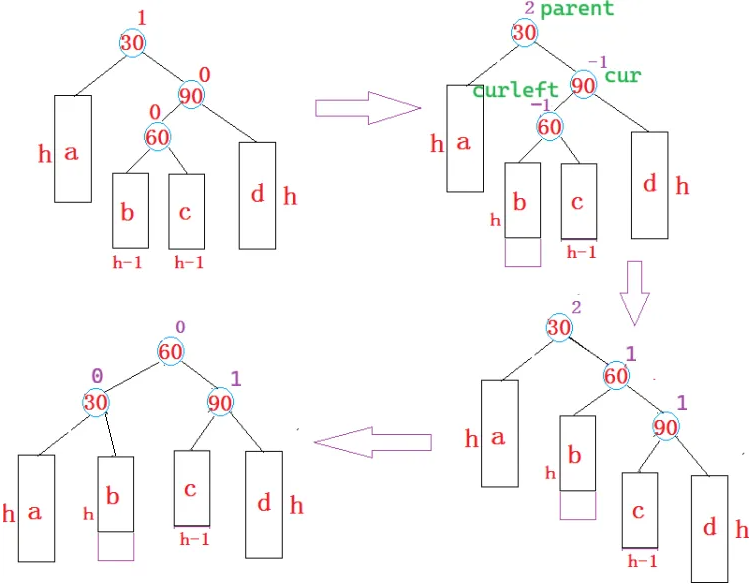
void RotateRL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

左右双旋

巧记：左边高就要向右压，本应右单旋，折线，就要先左单旋，再右单旋
        最下面的节点，把左右孩子给离它近的 cur、parent，自己当大哥

h == 0：60 自己是新插入的节点

h > 0：

1. 插入到 b 引发左右旋转

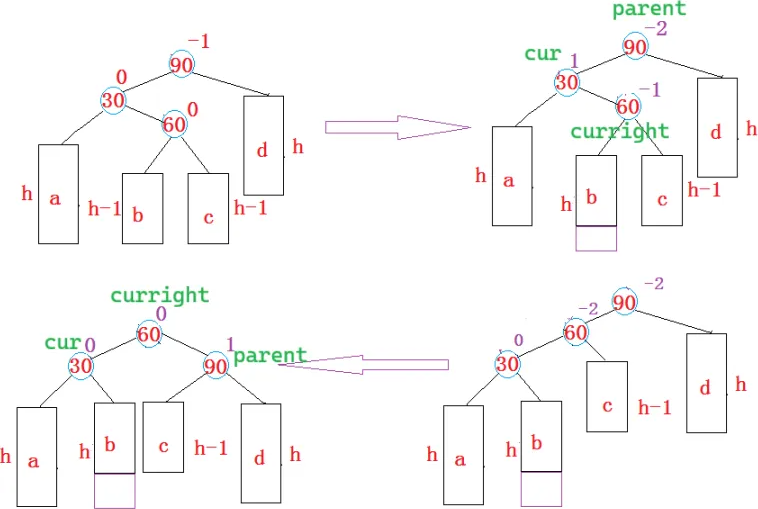
2. 插入到 c 引发左右旋转

void RotateLR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){cur->_bf = 0;curright->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = -1;curright->_bf = 0;parent->_bf = 0;}else if (bf == -1){cur->_bf = 0;curright->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

2. AVL 树的验证

有时程序有 bug，且数据量大，我们不可能挨着用眼睛瞅
可以写程序辅助调试，让程序帮忙看，即：写程序判断是不是 AVL 树

int Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;int leftHeight = Height(root->_left); // 自己求左子树的高度int rightHeight = Height(root->_right); // 自己求右子树的高度if (rightHeight - leftHeight != root->_bf) // 自己验证平衡因子是否正确{cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHeight - leftHeight) < 2 // 当前的平衡因子正确&& IsBalance(root->_left) // 并且左子树的平衡因子正确&& IsBalance(root->_right); // 并且右子树的平衡因子正确
} // 则说明整棵树是平衡树

Test.cpp

int main()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t;for (auto e : a){if (e == 15){int x = 0;}t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;}return 0;
}

如果锁定了插入哪个节点时导致平衡因子异常（出错）就写上 8-11 行，在第 10 行打断点，可以手动改条件断

int main()
{const int N = 10000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));//cout << "Insert:" << e << "->" << t.IsBalance() << endl;}cout << t.IsBalance() << endl;return 0;
}

三. 整体代码

AVLTree.h

template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){ }
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;cur->_parent = parent;// 更新平衡因子、判断是否控制平衡while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0) // 更新结束{break;}else if (parent->_bf == 1 || parent->_bf == -1) // 继续往上更新{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2) // 子树不平衡，需要旋转{if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent); // 单纯的右边高，左单旋}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent); // 单纯的左边高，右单旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent); // 右左双旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent); // 左右双旋}break;}else{assert(false);}}return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;// 2个核心步骤parent->_right = curleft;cur->_left = parent;if (curleft) // 调整curleft父亲节点的指向{curleft->_parent = parent;}parent->_parent = cur; //调整parent父亲节点的指向//cur->_parent = ppnode; 错：ppnode还要和cur建立关系//调整cur父亲节点的指向if (_root == parent){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = cur;elseppnode->_right = cur;cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;// 2个核心步骤parent->_left = curright;cur->_right = parent;parent->_parent = cur; // 调整parent父亲节点的指向if (curright) // 调整curright父亲节点的指向{curright->_parent = parent;}//cur->_parent = ppnode; 错：ppnode还要和cur建立关系// 调整cur父亲节点的指向if (_root == parent){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){cur->_bf = 0;curright->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = -1;curright->_bf = 0;parent->_bf = 0;}else if (bf == -1){cur->_bf = 0;curright->_bf = 0;parent->_bf = 1;}else{assert(false);}}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHeight = Height(root->_left); // 自己求左子树的高度int rightHeight = Height(root->_right); // 自己求右子树的高度if (rightHeight - leftHeight != root->_bf) // 自己验证平衡因子是否正确{cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHeight - leftHeight) < 2 // 当前的平衡因子正确&& IsBalance(root->_left) // 并且左子树的平衡因子正确&& IsBalance(root->_right); // 并且右子树的平衡因子正确} // 则说明整棵树是平衡树private:Node* _root = nullptr;
};

本篇的分享就到这里了，感谢观看，如果对你有帮助，别忘了点赞+收藏+关注。
小编会以自己学习过程中遇到的问题为素材，持续为您推送文章

http://www.dtcms.com/a/606423.html

相关文章：

  • c++之基础A（无返回函数）第三课
  • 温州网站建设温州网站制作百度禁止seo推广
  • 南宁市网站开发公司电话wordpress wp-login
  • 合肥制作手机网站中国供求网
  • Nine.fun｜从极致用户体验到社区自治的价值闭环
  • 淘宝客做的最好的网站怎么弄一个网站平台
  • 华为OD机试 双机位A卷 - 项目排期 / 最少交付时间 (JAVA Python C++ JS GO)
  • websocket操作入门
  • Golang学习笔记：定时crontab
  • Go语言编译器源码分析
  • LeetCode hot100:021 合并两个有序链表：两种解法的深入剖析
  • 做二手车网站需要什么手续费wordpress 批量换
  • 【基于 Spring Cloud Alibaba 的微服务电商项目】完整实现思路
  • 2025中国密码学会年会“人才培养论坛”成功举办，产学共探密码人才培育新路径
  • 高质量网站外链建设大揭秘网址收录大全
  • 网站建设的数字化和互联网化建设局工作怎么样
  • resource 和 K8S 对接部分 apifox
  • C语言编译器下载地址 | 提供多种C语言编译工具下载链接与使用指南
  • 网站备案跟网安备案区别展厅设计制作
  • 公司建立网站流程图开原网站制作
  • Python工程师的职业发展路径：专家访谈
  • 研发管理知识库（8）Terraform 简介
  • 网站后台常用密码工业设计公司如何选择
  • 做民宿的网站有哪些抖音代运营大概多少钱一个月
  • C++模块化项目构建入门教
  • Ansible Playbook入门指南：核心语法与实战
  • 苏州高端网站建设设计公司哪家好wordpress 多个页面
  • 云手机是真实手机吗
  • 制作网站的详细步骤江阴便宜做网站
  • 建设局考试通知文件网站苏州工业园区有哪些企业