当前位置：首页 > news >正文

div2 1052 个人补题笔记

news 2025/11/14 7:44:34

链接：Dashboard - Codeforces Round 1052 (Div. 2) - Codeforces

D1+D2

A

思路：

统计每个数出现的个数，然后排一下序，设出现次数定为 $x$ ，对于元素 $i$ ，若是 $cnt_{i}\geqslant x$ ，则就对元素 $i$ 选 $x$ 个，若是 $cnt_{i}< x$ ，则就对元素 $i$ 选 $x$ 个。

根据这个思路，我们把每个元素出现的次数 $cnt_{i}$ 按从大到小排序，我们的答案即是 $max(cnt_{i}*i)$ 。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int cnt[N];
bool cmp(int a,int b){return a>b;
}
void solve(){int n;cin>>n;for(int i=1;i<=n;i++)cnt[i]=0;for(int i=1;i<=n;i++){int x;cin>>x;cnt[x]++;}int ans=0;sort(cnt+1,cnt+n+1,cmp);for(int i=1;i<=n;i++){ans=max(ans,cnt[i]*i);}cout<<ans<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

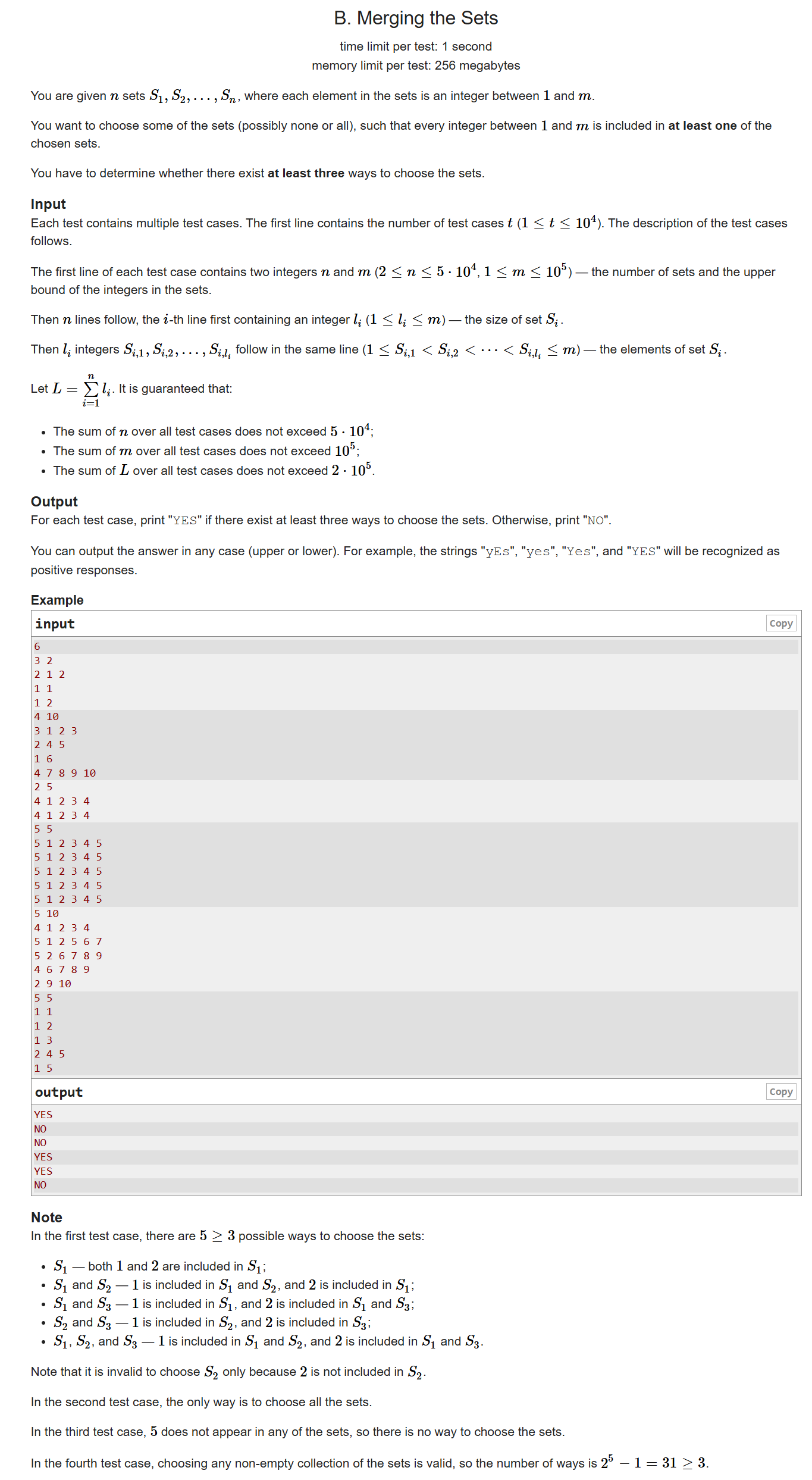
B

思路：

对于可能构造的方案，首先，所有 $S$ 都选择是一种方案，然后所有 $S$ 中删除一个 $S_{i}$ 也是一种方案，这样我们就有了 $n+1$ 种方案，其他方案成立的前提是以上 $n+1$ 种方案是否至少有 $3$ 种方案成立，因此只需看这 $n+1$ 种方案即可。

我们可以开个 $vector<vector<int>>$ 数组 $cun$ ，然后我们把每一组的元素都存起来，设 $cnt_{i}$ 为元素 $i$ 出现的次数。

我们看少了一组方案的元素后，对于任意一个元素 $i$ ，是否出现 $cnt_{i}=0$ 的情况，如果没有出现即可说明这种方案是成立的，我们只需要有 $2$ 种这种方案即可说明存在。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int cnt[N];
int n,m;
void solve(){cin>>n>>m;for(int i=1;i<=m;i++)cnt[i]=0;vector<vector<int> >cun(n+1);for(int i=1;i<=n;i++){int s;cin>>s;for(int j=1;j<=s;j++){int x;cin>>x;cnt[x]++;cun[i].push_back(x);}}int sum=0;for(int i=1;i<=n;i++){bool st=false;for(auto c:cun[i]){if(cnt[c]==1){st=true;break;}}if(!st)sum++;}for(int i=1;i<=m;i++)if(cnt[i]==0)sum=0;if(sum>=2)cout<<"YES"<<'\n';elsecout<<"NO"<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

C

思路：

朴素想法：

对于 $s_{i}=1$ 的 $i$ ，我们要想让其能二分找到，就要确保 $p_{i}=i$ ，且对于所有的 $j<i$ ，满足 $p_{j}<p_{i}$ 。

对于 $s_{i}=1$ 的 $i$ 的 $i$ ，我们只需要不满足上述条件即可。

在实现上，设 $s_{0}=s_{n+1}=1$ ，若是对于 $1\leqslant i\leqslant n$ ，存在 $s_{i}=0$ ， $s_{i-1}=s_{i+1}=1$ ，说明这种情况肯定不存在。

若是存在方案，我们先使 $p_{i}=i$ ，对于 $s_{l}=s_{r}=1$ ，且 $l\leqslant i\leqslant r$ ，都满足 $s_{i}=0$ 时候，我们对 $[l+1,r-1]$ 区间的元素翻转存储即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n;
int a[N];void solve(){string s;cin>>n;cin>>s;s="1"+s+"1";for(int i=1;i<=n;i++){if(s[i]=='0'&&s[i-1]=='1'&&s[i+1]=='1'){cout<<"NO"<<'\n';return ;}}cout<<"YES"<<'\n';int id=1;for(int i=1;i<=n+1;i++){if(s[i]=='1'){a[i]=i;int x=i-1;for(int j=id;j<i;j++){a[j]=x--;}            id=i+1;}}for(int i=1;i<=n;i++){cout<<a[i]<<' ';}cout<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

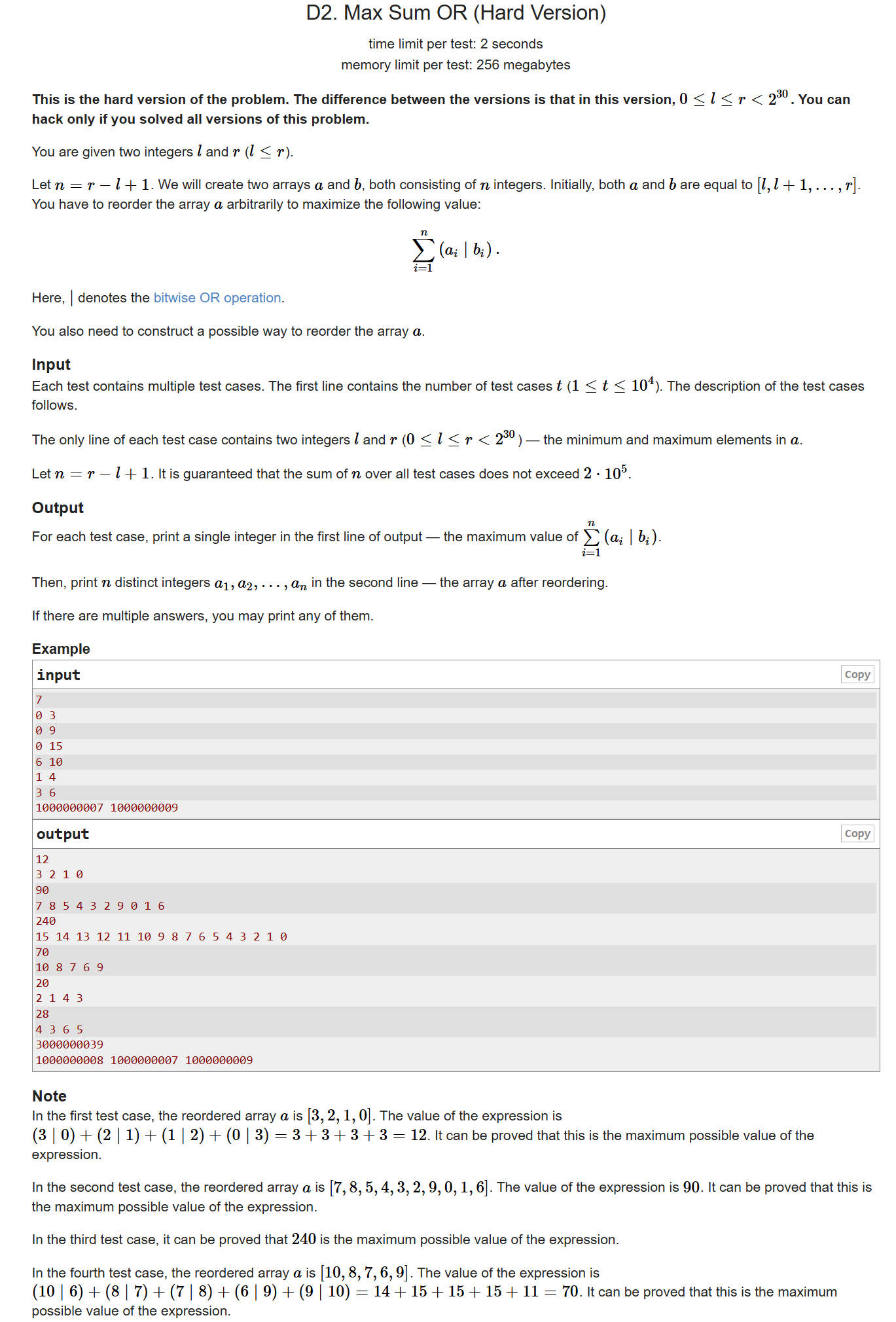
D1+D2

思路：
对于 $D1$ 而言，在 $[0,r]$ 中对于每一个数 $x$ ，必然存在唯一一个数 $y$ ，让最终解最大。

假设一个数的二进制为 $110010$ ，那么和其匹配的必然是 $XXX...001101$ ，我们可以从大到小枚举，对于每个形如 $110010$ 这类未配对的数，我们找形如 $001101$ 的与其配对。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
typedef long long ll;
ll a[N];
bool st[N];
int l,r;void solve(){cin>>l>>r;for(int i=0;i<=r;i++)st[i]=false;for(int i=r;i>=0;i--){if(st[i])continue;int x=0;bool k=false;for(int j=20;j>=0;j--){int c=1<<j;if((i&c)){k=true;continue;}else if(k)x+=c;}st[x]=st[i]=true;a[i]=x;a[x]=i;}ll ans=0;for(int i=0;i<=r;i++)ans+=(ll)i|a[i];cout<<ans<<'\n';for(int i=0;i<=r;i++)cout<<a[i]<<' ';cout<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

对于 $D2$ 而言，可以发现， $2^{k}$ 与 $2^{k}-1$ 匹配时是最好的， $2^{k}+1$ 与 $2^{k}-2$ 是最优的 $......$

根据这个基本想法，我们可以每次对 $[l,r]$ 的 $r$ 和 $l$ 先按二进制拆分，然后我们要找满足如下条件的最大的 $d$ ：

$r_{d}=1$ 且 $l_{d}=0$ ，然后我们把 $r_{j}(j\geq d)$ 都提出来设为 $k$ ，设 $i=k,j=k-1$ 。

我们划分为 $[l,j]$ 和 $[i,r]$ 两个区间，依次按照 $i$ 匹配 $j$ ， $i+1$ 匹配 $j-1$ $......$ 的思路完成匹配，最后有以下三种情况：

（1） $j-l+1>r-i+1$ ,设 $[l,j_{1}]$ 没有匹配，则把 $r=j_{1}$ 再按照上述递归处理即可。

（2） $j-l+1<r-i+1$ ,设 $[i_{1},r]$ 没有匹配，则把 $l=i_{1}$ 再按照上述递归处理即可。

（3） $j-l+1=r-i+1$ ,说明匹配完成，结束递归即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
typedef long long ll;
map<ll,ll>a;
ll l,r;int cal(int x,int cnt){ll c=0;for(ll i=30;i>=0;i--){ll r=(ll)1<<i;if(x&r){cnt--;c+=r;}if(cnt==0)return c;}return c;
}void check(int l,int r,int d){if(l>=r) {if(l==r)a[l]=l;return ;}while(cal(l,d)==cal(r,d))d++;ll k=cal(r,d);ll i=k,j=k-1;    for(;i<=r&&j>=l;i++,j--){a[i]=j;a[j]=i;}if(i<=r)check(i,r,d);else check(l,j,d);
}   void solve(){cin>>l>>r;check(l,r,1);ll ans=0;for(int i=l;i<=r;i++)ans+=(i|a[i]);cout<<ans<<'\n';for(int i=l;i<=r;i++)cout<<a[i]<<' ';cout<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

E

思路：

对于区间 $[l,r]$ ，假设 $x$ 在区间 $[l,r]$ 中没有出现过该元素，我们定义 $cnt_{x}$ 为 $a_{i}>x~~(l\leqslant i\leqslant r)$ 中满足条件的 $i$ 的个数。

我们可以证明的是， $cnt_{x}<=cnt_{mex(b_{l}...b_{r})}$ 是必然的，因为对于 $cnt_{x}$ 而言， $x$ 越小， $cnt_{x}$ 越大，而 $mex(b_{l}...b_{r})$ 是最小的 $x$ 。

假设 $a_{p}=x$ ，且对于任意的 $p< i\leqslant r$ ， $a_{i}\neq x$ ，则 $[p+1,r]$ 就是右区间为 $r$ ，且满足要求的情况下最大的 $cnt_{x}$ 。

所以，对于每个定值右区间 $r$ ，我们需要维护，去找每一个可能的 $x$ 对应的 $cnt_{x}$ 。

我们可以使用线段树来维护，具体流程：

（1）对于每个定值右区间 $r$ ，对于 $x<a_{r}$ 的 $cnt_{x}$ 而言，我们相当于让 $cnt_{x}=cnt_{x}+1$ 。

（2）而对于 $a_{r}$ 这个点而言，由于到 $r$ 时候 $x=a_{r}$ 是不满足要求的，所以要把这时候的 $cnt_{a_{r}}=0$ 。

然后每一次查询输出最大的 $cnt_{x}$ 。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+100;
typedef long long ll;
ll tr[N],lz[N];
int n;void build(int l,int r,int u){tr[u]=lz[u]=0;if(l==r)return ;int mid=(l+r)/2;build(l,mid,2*u+1);build(mid+1,r,2*u+2);
}void modify(int L,int R,int l,int r,int u){if(L<=l&&r<=R){tr[u]++;lz[u]++;return ;}int mid=(l+r)/2;if(mid>=L)modify(L,R,l,mid,2*u+1);if(mid<R)modify(L,R,mid+1,r,2*u+2);tr[u]=max(tr[2*u+1],tr[2*u+2])+lz[u];
}void point(int x,int l,int r,int u,int val){if(l==r){tr[u]=-val;return ;}int mid=(l+r)/2;val+=lz[u];if(x<=mid)point(x,l,mid,2*u+1,val);elsepoint(x,mid+1,r,2*u+2,val);tr[u]=max(tr[2*u+1],tr[2*u+2])+lz[u];
}void solve(){cin>>n;build(0,n,0);for(int i=1;i<=n;i++){int x;cin>>x;modify(0,x,0,n,0);point(x,0,n,0,0);cout<<tr[0]<<' ';}cout<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

至于之后2900的F，感觉目前能力达不到，就不补了

查看全文

http://www.dtcms.com/a/605744.html