当前位置：首页 > news >正文

【动手学深度学习】8.1. 序列模型

news 2025/11/14 7:42:33

8. 循环神经网络（RNN）

目前为止，我们已学习了处理表格数据和图像数据的模型。其中，卷积神经网络（CNN）通过捕捉局部空间结构，成功建模图像中像素的相对位置关系。然而，许多现实数据具有序列结构，如文本、语音、视频帧或时间序列，其元素顺序至关重要——打乱顺序将破坏语义或时序逻辑。

更重要的是，这类数据通常不满足独立同分布（i.i.d.）假设。相反，当前时刻的输出往往依赖于历史信息。例如：

文本中的下一个词取决于前面的上下文；
股价变化受过去走势影响；
用户行为序列中蕴含动态偏好。

为有效建模此类序列数据，我们需要能够记忆历史信息并随时间动态处理输入的模型。这正是循环神经网络（Recurrent Neural Network, RNN） 的设计初衷。

RNN通过引入隐藏状态（hidden state） 作为时间上的记忆单元，将前一时刻的状态与当前输入结合，以生成当前输出和新的状态。这种“循环”机制使网络具备了处理变长序列和捕捉长期依赖的潜力。

序列数据建模基础：回顾序列数据的特点与挑战；
文本预处理技术：包括分词、构建词汇表、序列编码等；

本章将围绕以下内容展开：

语言模型原理：介绍如何建模下一个词的概率，作为RNN的典型应用；
RNN结构设计：从循环机制到具体前向传播过程；
训练难点分析：探讨RNN中的梯度计算（如通过时间的反向传播，BPTT）及其面临的梯度消失/爆炸问题。

简言之，如果说CNN是处理空间结构的利器，那么RNN则是建模时间或序列结构的基础性网络架构。本章将为后续更强大的序列模型（如LSTM、GRU和Transformer）奠定理论与实践基础。

8.1. 序列模型

电影评分并非固定不变，而是随时间动态演变。心理学揭示了多种影响因素：

锚定（anchoring）效应：评分受他人意见或外部事件影响。例如，奥斯卡获奖后，电影评分显著上升，即使影片本身未变。这种效应可持续数月，使评分提高半点以上（Wu et al., 2017）。
享乐适应（hedonic adaptation）：观众在经历高质量电影后，会迅速调整期望，导致对普通影片评价降低。
季节性（seasonality）：观影偏好具有时间规律，如八月很少有人观看圣诞题材电影。
社会争议：导演或演员的不当行为可能导致电影口碑下滑。
“烂片”文化：某些电影因极度糟糕而走红，如《Plan 9 from Outer Space》和《Troll2》，成为小众经典。

因此，引入时间动力学（temporal dynamics） 可提升推荐系统准确性（Koren, 2009）。序列数据的重要性不仅限于电影评分，还广泛存在于其他场景：

用户行为模式：学生放学后社交媒体使用激增，股市软件在交易时段更活跃。
预测挑战：预测明日股价（外推法, extrapolation）比估计历史数据（内插法, interpolation）更难。
连续内容：音乐、语音、文本和视频的意义依赖顺序。例如，“狗咬人”与“人咬狗”字相同，但语义和冲击力截然不同。
地震序列：大地震后常引发时空密集的余震（aftershocks），其强度和频率显著高于随机事件。
社交互动：微博上的争论和辩论也呈现时间连续性和动态演化。

综上所述，序列结构和时间演化对建模用户行为、自然现象和社会动态至关重要。

1）统计工具

处理序列数据需要统计工具和新的深度神经网络架构。为了简单起见，我们以下图所示的股票价格（富时100指数）为例。

图8.1.1 近30年的富时100指数

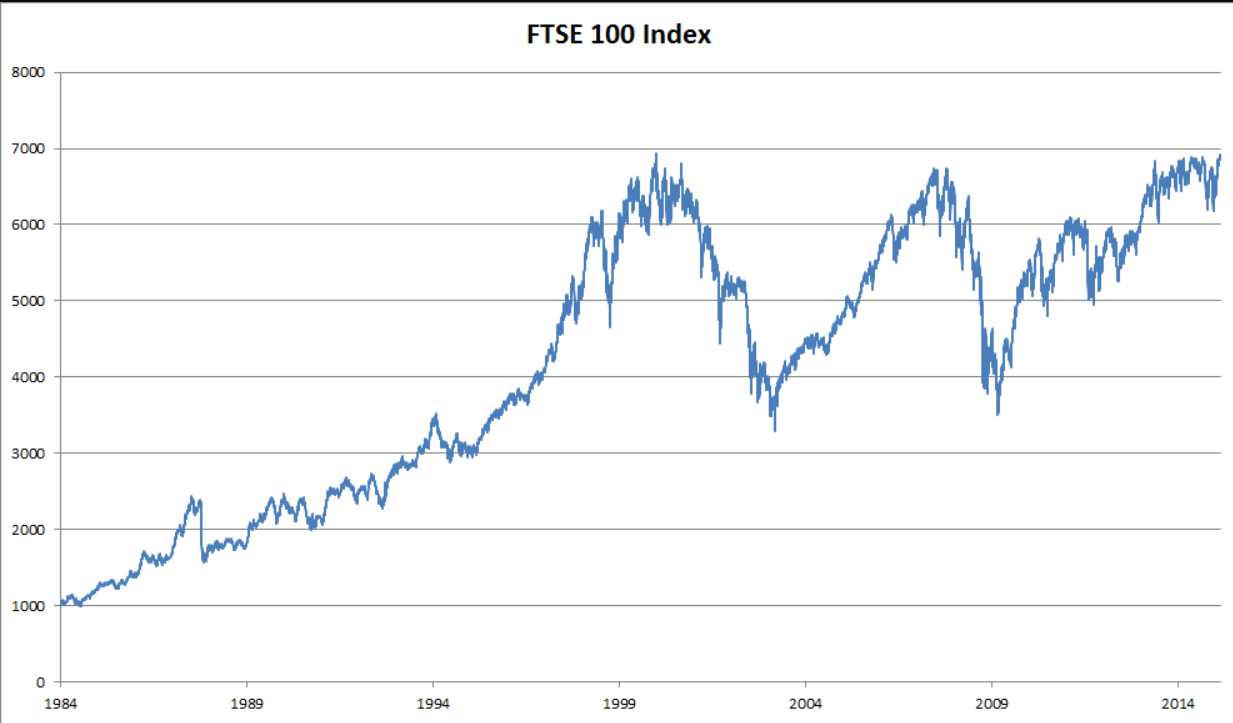
在这里插入图片描述

其中，用 $x_t$ 表示价格，即在时间步（time step） $\in \mathbb{Z}^+$ 时，观察到的价格 $x_t$ 。请注意， $t$ 对于本文中的序列通常是离散的，并在整数或其子集上变化。假设一个交易员想在 $t$ 日的股市中表现良好，于是通过以下途径预测 $x_t$ ：

$x_t \sim P(x_t \mid x_{t-1}, \ldots, x_1). \tag{8.1.1}$

公式本质：

在时间序列中，当前值 $x_t$ 不是独立的，而是由过去所有值共同决定的，其分布为条件概率 $P(x_t∣x_{t−1},…,x_1)$ 。

（1）自回归模型

在序列预测中，直接估计 $P(x_t \mid x_{t-1}, \ldots, x_1)$ 面临主要问题：输入数据的数量，随t增加而增加。为了高效估计条件概率，平衡计算复杂度与预测准确性。主要解决策略有两种：

a.自回归模型（Autoregressive Models）

仅使用最近 $\tau$ 个观测值： $x_{t-1}, \ldots, x_{t-\tau}$
优势：参数数量固定，适合深度网络训练
本质：对自身历史数据进行回归

b.隐变量自回归模型（Latent Autoregressive Models）

维护隐藏状态 $h_t$ 总结历史信息
通过两个公式工作：
- 预测： $\hat{x}_t = P(x_t \mid h_t)$ ，（即，预测值 $\hat{x}_t$ = 在给定隐状态 $h_t$ 的条件下，观测值 $x_t$ 的概率分布）
- 状态更新： $h_t = g(h_{t-1}, x_{t-1})$
特点： $h_t$ 为隐变量，不直接观测

图8.1.2 隐变量自回归模型

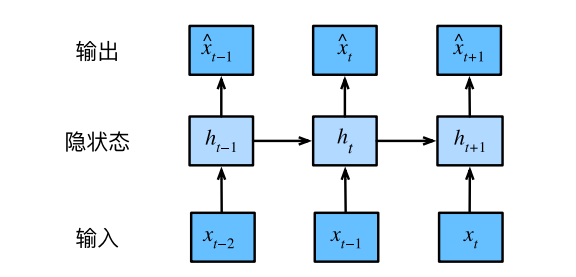
在这里插入图片描述

c.如何生成训练数据？

背景：时间序列模型（比如预测股票价格、天气）需要训练数据，但未来数据还没发生，怎么训练？
关键矛盾：*“不能用未来的数据训练模型，但模型又要预测未来。”*→ 解决方案：用历史数据模拟“预测未来”的过程。

关键假设：序列规律不变（平稳性）

概念：*“序列本身的动力学不会改变… 统计学家称不变的动力学为静止的（stationary）”*→ 通俗解释：假设“过去和未来的规律是相同的”。
例如：预测明天的天气时，假设天气变化的规律（比如“雨天后常有晴天”）和过去一样。
如果规律突然变了（比如新发明了人工降雨技术），预测就失效了。

专业术语：

动力学（Dynamics） = 数据变化的规律（比如趋势、周期性）。
平稳性（Stationary） = 规律不变（不是“静止”，而是“稳定”）。

如何分解序列概率？

公式 (8.1.2)：
$P(x_1, \dots, x_T) = \prod_{t=1}^T P(x_t \mid x_{t-1}, \dots, x_1)$
为什么这样分解？
- 直接预测整个序列 (P(x_1,…,x_T)) 计算量爆炸（比如预测30天天气，可能性有 (2^{30}) 种）。
- 拆成条件概率后：每一步只需关注“最近历史”，计算量大幅降低。

离散 vs. 连续数据的处理差异

概念：“对于离散的对象（如单词），需要使用分类器而不是回归模型”
关键点：
- 无论是连续还是离散数据，概率分解公式 $P(x_t \mid \text{历史})$ 都适用。
- 区别仅在预测方式：
  - 连续数据 → 用回归模型输出具体数值（如预测明天温度 26℃）
  - 离散数据 → 用分类模型输出概率分布（如预测明天 70% 概率下雨，30% 晴天）

总结一句话：“用昨天的规律预测今天，再用今天的规律预测明天”—— 这就是时间序列模型训练的本质。

（2）马尔可夫模型

马尔可夫模型核心思想：未来只依赖于现在，与过去无关

在自回归近似中，若用最近的 $\tau$ 个历史值 $x_{t-1},\dots,x_{t-\tau}$ 而非全部历史来预测 $x_t$ 是足够精确的，则称序列满足马尔可夫条件（Markov condition）。

特别地，当 $\tau = 1$ 时，得到一阶马尔可夫模型，联合概率可分解为：

$P(x_1, \ldots, x_T) = \prod_{t=1}^T P(x_t \mid x_{t-1}), \quad \text{其中 } P(x_1 \mid x_0) := P(x_1).$

当 $x_t$ 为离散变量时，该模型尤为高效：利用动态规划可精确计算，如 $P(x_{t+1} \mid x_{t-1})$ 等边际概率：

$P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1} \mid x_t) P(x_t \mid x_{t-1}),$

这依赖于马尔可夫性质： $P(x_{t+1} \mid x_t, x_{t-1}) = P(x_{t+1} \mid x_t)$

此类动态规划方法在隐马尔可夫模型、控制与强化学习中广泛应用（详见第9.4节）。

（3）因果关系

核心思想：**时间有方向，因果有顺序。**数学上可以倒着算，但现实中时间不会倒流

虽然联合分布 $P(x_1, \ldots, x_T)$ 理论上可按任意顺序分解（包括倒序）：

$P(x_1, \ldots, x_T) = \prod_{t=T}^1 P(x_t \mid x_{t+1}, \ldots, x_T),$

但在时序数据中，时间具有自然的前向因果方向：过去影响未来，但未来不能影响过去。

因此，改变 $x_t$ 可能影响 $x_{t+1}$ ，但不会改变基于过去观测的分布。这使得前向条件概率 $P(x_{t+1} \mid x_t)$ 更具因果解释性，也更易建模。例如，常可写出生成式关系 $x_{t+1} = f(x_t) + \epsilon$ ，其中 $\epsilon$ 为噪声，而反向关系通常不可行。

这种前向因果结构正是大多数时序建模所关注的方向（详见 Peters et al., 2017）。

2）训练

在了解了上述统计工具后，让我们在实践中尝试一下！首先，我们生成一些数据：使用正弦函数和一些可加性噪声来生成序列数据，时间步为1, 2, … , 1000。

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2lT = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

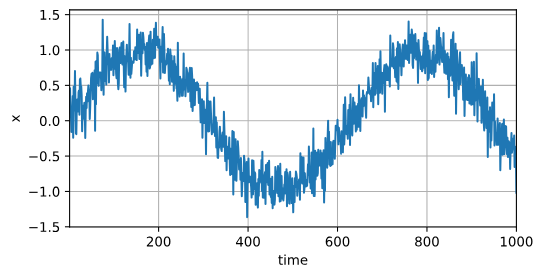
在这里插入图片描述

接下来，将这个序列转换为模型的特征－标签（feature-label）对。基于嵌入维度 $\tau$ ，我们将数据映射为数据对 $y_t = x_t$ 和 $\mathbf{x}_t = [x_{t-\tau}, \ldots, x_{t-1}]$ 。这比我们提供的数据样本少了 $\tau$ 个，因为我们没有足够的历史记录来描述前 $\tau$ 个数据样本。一个简单的解决办法是：如果拥有足够长的序列就丢弃这几项；另一个方法是用零填充序列。在这里，我们仅使用前600个“特征－标签”对进行训练。

tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),batch_size, is_train=True)

在这里，我们使用一个相当简单的架构训练模型：一个拥有两个全连接层的多层感知机，ReLU激活函数和平方损失。

# 初始化网络权重的函数
def init_weights(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)# 一个简单的多层感知机
def get_net():net = nn.Sequential(nn.Linear(4, 10),nn.ReLU(),nn.Linear(10, 1))net.apply(init_weights)return net# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

现在，准备训练模型了。实现下面的训练代码的方式与前面几节（如 3.3节）中的循环训练基本相同。因此，我们不会深入探讨太多细节。

def train(net, train_iter, loss, epochs, lr):trainer = torch.optim.Adam(net.parameters(), lr)for epoch in range(epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, 'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')net = get_net()
train(net, train_iter, loss, 5, 0.01)# 输出：
epoch 1, loss: 0.076846
epoch 2, loss: 0.056340
epoch 3, loss: 0.053779
epoch 4, loss: 0.056320
epoch 5, loss: 0.051650

3）预测

由于训练损失很小，因此我们期望模型能有很好的工作效果。让我们看看这在实践中意味着什么。首先是检查模型预测下一个时间步的能力，也就是单步预测（one-step-ahead prediction）。

onestep_preds = net(features)
d2l.plot([time, time[tau:]],[x.detach().numpy(), onestep_preds.detach().numpy()], 'time','x', legend=['data', '1-step preds'], xlim=[1, 1000],figsize=(6, 3))

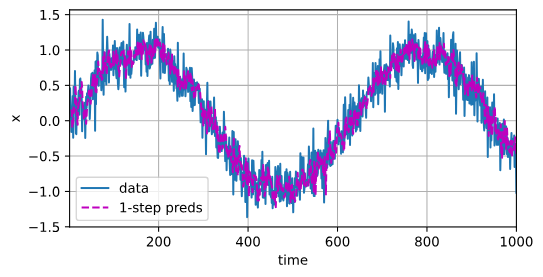
在这里插入图片描述

正如我们所料，单步预测效果不错。即使这些预测的时间步超过了(600+4)（n_train + tau），其结果看起来仍然是可信的。然而有一个小问题：如果数据观察序列的时间步只到604，我们需要一步一步地向前迈进：

$\begin{split}\hat{x}_{605} = f(x_{601}, x_{602}, x_{603}, x_{604}), \\ \hat{x}_{606} = f(x_{602}, x_{603}, x_{604}, \hat{x}_{605}), \\ \hat{x}_{607} = f(x_{603}, x_{604}, \hat{x}_{605}, \hat{x}_{606}),\\ \hat{x}_{608} = f(x_{604}, \hat{x}_{605}, \hat{x}_{606}, \hat{x}_{607}),\\ \hat{x}_{609} = f(\hat{x}_{605}, \hat{x}_{606}, \hat{x}_{607}, \hat{x}_{608}),\\ \ldots\end{split}$

通常，对于直到 $x_t$ 的观测序列，其在时间步(t+k)处的预测输出 $\hat{x}_{t+k}$ 称为k步预测（k-step-ahead-prediction）。由于我们的观察已经到了 $x_{604}$ ，它的k步预测是 $\hat{x}_{604+k}$ 。换句话说，我们必须使用我们自己的预测（而不是原始数据）来进行多步预测。让我们看看效果如何。

multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))d2l.plot([time, time[tau:], time[n_train + tau:]],[x.detach().numpy(), onestep_preds.detach().numpy(),multistep_preds[n_train + tau:].detach().numpy()], 'time','x', legend=['data', '1-step preds', 'multistep preds'],xlim=[1, 1000], figsize=(6, 3))

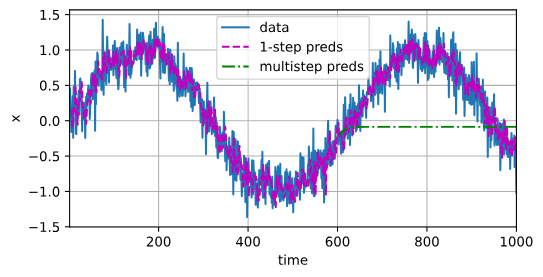
在这里插入图片描述

如上面的例子所示，绿线的预测显然并不理想。经过几个预测步骤之后，预测的结果很快就会衰减到一个常数。为什么这个算法效果这么差呢？

事实是由于错误的累积：假设在步骤1之后，积累了一些错误 $\epsilon_1 = \bar\epsilon$ 。于是，步骤2的输入被扰动了 $\epsilon_1$ ，结果积累的误差是依照次序的 $\epsilon_2 = \bar\epsilon + c \epsilon_1$ ，其中c为某个常数，后面的预测误差依此类推。因此误差可能会相当快地偏离真实的观测结果。

例如，未来24小时的天气预报往往相当准确，但超过这一点，精度就会迅速下降。我们将在本章及后续章节中讨论如何改进这一点。

基于 k = 1, 4, 16, 64，通过对整个序列预测的计算，让我们更仔细地看一下k步预测的困难。

max_steps = 64features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i<tau）是来自x的观测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau):features[:, i] = x[i: i + T - tau - max_steps + 1]# 列i（i>=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):features[:, i] = net(features[:, i - tau:i]).reshape(-1)steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],figsize=(6, 3))

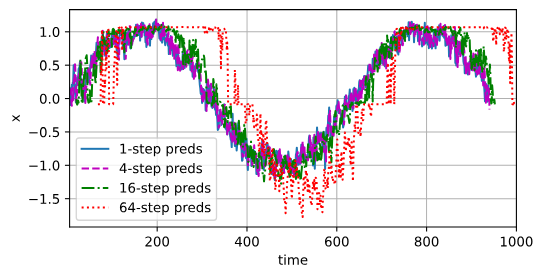
在这里插入图片描述

以上例子清楚地说明了当我们试图预测更远的未来时，预测的质量是如何变化的。虽然“(4)步预测”看起来仍然不错，但超过这个跨度的任何预测几乎都是无用的。

4）小结

内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。
序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。
对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。
对于直到时间步t的观测序列，其在时间步t+k的预测输出是“k步预测”。随着我们对预测时间k值的增加，会造成误差的快速累积和预测质量的极速下降。