当前位置：首页 > news >正文

C++进阶：（十）深度解析哈希表：原理、实现与实战

news 2025/11/14 6:35:57

前言

在数据结构的世界里，哈希表绝对是 “效率王者” 般的存在。无论是日常开发中的缓存设计、数据库索引，还是编程语言中的容器实现（比如 C++ STL 的 unordered_map），都离不开哈希表的身影。它以接近 O (1) 的平均时间复杂度完成增删查改操作，彻底打破了数组、链表等线性结构的性能瓶颈。

但很多开发者对哈希表的理解只停留在 “用着方便” 的层面，对于其背后的哈希函数设计、冲突解决机制、扩容策略等核心原理一知半解。本文将从底层原理出发，结合 C++ 代码实现，全方位拆解哈希表的设计思路与实战技巧，带你从 “会用” 到 “精通”，真正理解哈希表的本质。下面就让我们正式开始吧！

一、哈希表核心概念：什么是哈希？

1.1 哈希的本质：关键字与位置的映射

哈希（Hash）又称散列，本质是一种键值对存储的高效组织方式。它的核心思想的是通过一个 “哈希函数”，将数据的关键字（Key）直接映射到存储数组的某个位置（索引），这样查找时无需遍历整个容器，直接通过哈希函数计算位置就能快速定位数据，这也是哈希表高效的根源。

举个生活中的例子：我们在图书馆找书时，如果每本书都有一个唯一的编号，且编号直接对应书架的位置（比如编号 101 对应 1 排 0 列 1 层），那么我们无需逐排查找，直接根据编号找到位置即可 —— 这就是哈希表的核心逻辑。

在计算机中，这个 “编号对应位置” 的规则就是哈希函数，存储数据的数组就是哈希表的底层存储结构。

1.2 直接定址法：最简单的哈希实现

最直观的哈希函数是直接定址法，适用于关键字范围集中的场景。它的逻辑非常简单：直接用关键字本身（或关键字的线性变换）作为存储位置的下标。

比如：

关键字范围是 [0,99] 的整数集合：直接用关键字作为数组下标（Key=5 → 下标 5）；
关键字是 [a,z] 的小写字母：用字母的 ASCII 码减去 'a' 的 ASCII 码作为下标（'a'→0，'b'→1，…，'z'→25）。

这种方法在实际开发中是很常见的，比如387. 字符串中的第一个唯一字符这道题，就可以用直接定址法快速统计字符出现次数：

class Solution {
public:int firstUniqChar(string s) {// 26个小写字母对应下标0-25，存储出现次数int count[26] = {0};// 统计每个字符出现次数for (auto ch : s) {count[ch - 'a']++;}// 找到第一个出现次数为1的字符下标for (size_t i = 0; i < s.size(); ++i) {if (count[s[i] - 'a'] == 1) {return i;}}return -1;}
};

直接定址法的优点是无冲突、效率极高，但缺点也很明显：如果关键字范围分散（比如关键字是 [1, 1000000] 的 10 个随机数），会导致数组空间极度浪费，甚至内存不足。这时候就需要更灵活的哈希函数设计。

1.3 哈希冲突：无法避免的 “小插曲”

当我们用哈希函数将关键字映射到有限大小的数组时，必然会出现 “两个不同的关键字映射到同一个下标” 的情况 —— 这就是哈希冲突（也称哈希碰撞）。

比如：用 “关键字对 11 取模” 作为哈希函数（M=11），关键字 19 和 30 的计算结果都是 8（19%11=8，30%11=8），这就产生了冲突。

理想情况下，我们希望哈希函数能让关键字均匀分布在数组中，减少冲突，但实际场景中冲突无法完全避免—— 就像图书馆的书架位置有限，总会有新书的编号对应已被占用的位置。因此，哈希表的设计核心包含两部分：

设计优秀的哈希函数，减少冲突次数；
设计高效的冲突解决机制，处理已发生的冲突。

1.4 负载因子：哈希表的 “拥挤程度”

负载因子（Load Factor）是衡量哈希表拥挤程度的核心指标，直接影响冲突概率。它的定义如下：

负载因子 α = 哈希表中存储的元素个数（N） / 哈希表的数组大小（M）

负载因子与哈希表性能的关系是：

α 越大：哈希表越拥挤，冲突概率越高，查询效率越低；
α 越小：哈希表越宽松，冲突概率越低，但空间利用率越低。

不同冲突解决机制对应的负载因子阈值不同：

开放定址法：α 必须小于 1（因为所有元素都存储在数组中，数组满了就无法插入）；
链地址法：α 可以大于 1（冲突元素会以链表形式挂在数组下标下），STL 的 unordered_map 默认将 α 阈值设为 1，超过则扩容。

二、哈希函数设计：如何让关键字 “均匀分布”？

哈希函数的核心目标是让关键字等概率、均匀地分布在哈希表的数组中，从而最小化冲突。常用的哈希函数设计方法有多种，各有适用场景，下面重点讲解实战中最常用的几种。

2.1 除法散列法（除留余数法）：最常用的哈希函数

除法散列法是实战中应用最广泛的哈希函数，逻辑简单、实现高效。它的定义是：

给定哈希表数组大小 M，对于关键字 Key，哈希函数为：h (Key) = Key % M。本质其实是通过取模运算，将关键字映射到 [0, M-1] 的范围内。

关键设计要点：M 的选择

M 的取值是直接影响哈希分布的均匀性的，它有两个核心原则：

避免选择 2 的整数次幂（如 16、32、64）：如果 M 是 2^k，那么取模运算本质是保留 Key 的后 k 位二进制，容易导致冲突（比如 63 和 31 的后 4 位都是 1111，M=16 时哈希值都是 15）；
避免选择 10 的整数次幂（如 100、1000）：会导致哈希值只依赖 Key 的后几位（比如 112 和 12312，M=100 时哈希值都是 12）；

推荐选择不太接近 2 的整数次幂的质数（如 53、97、193）：质数的因子少，能让关键字分布更均匀，减少冲突。

特殊情况：Java HashMap 的优化

虽然理论上推荐 M 为质数，但 Java 的 HashMap 却选择 M 为 2 的整数次幂 —— 这是为了用位运算替代取模运算（位运算比取模更快）。它的优化逻辑是：

将 Key 的哈希值右移 16 位（高位参与运算），再与 Key 本身异或，最后用 “& (M-1)” 替代取模（M 是 2^k 时，Key & (M-1) 等价于 Key % M）：

h(Key) = (Key ^ (Key >> 16)) & (M - 1)

这种设计既保证了效率，又通过高位异或让哈希值分布更均匀，是理论与实战的灵活结合。

2.2 乘法散列法：不依赖 M 的取值

乘法散列法对 M 的取值没有限制，核心是通过常数因子将关键字映射到均匀分布的区间。它的步骤如下：

选择一个常数 A（0 <A < 1），推荐取黄金分割点 A = (√5 - 1)/2 ≈ 0.6180339887；
计算 Key 与 A 的乘积，提取小数部分；
用 M 乘以该小数部分，向下取整得到哈希值。

数学表达式为：h (Key) = floor (M × ((A × Key) % 1.0))

示例计算

假设 M=1024，Key=1234，A=0.6180339887：

A × Key = 0.6180339887 × 1234 ≈ 762.653942；
小数部分为 0.653942；
M × 小数部分 = 1024 × 0.653942 ≈ 669.636；
向下取整得到 h (Key)=669。

乘法散列法的优点是 M 可以任意取值（比如 2 的整数次幂、10 的整数次幂），但缺点是计算稍复杂，效率不如除法散列法，实战中是应用较少的。

2.3 全域散列法：抵御恶意攻击

如果哈希函数是固定的，恶意攻击者可能构造出所有关键字都映射到同一个下标的数据集（比如故意选择后 k 位相同的 Key），导致哈希表退化为链表，查询效率降至 O (n)。

全域散列法是通过随机选择哈希函数来解决这个问题的，核心逻辑是：

选择一个足够大的质数 P；
随机选择 a（1 ≤ a ≤ P-1）和 b（0 ≤ b ≤ P-1）；
哈希函数为：h_ab (Key) = ((a × Key + b) % P) % M。

每次初始化哈希表时，随机选择一组 (a,b)，后续所有增删查改都使用该哈希函数 —— 这样攻击者无法提前预知哈希函数，也就无法构造恶意数据集。

示例计算

假设 P=17，M=6，a=3，b=4，Key=8：h_34 (8) = ((3×8 + 4) % 17) % 6 = (28 % 17) % 6 = 11 % 6 = 5。

2.4 关键字非整数的处理：仿函数转换

前面的哈希函数都假设 Key 是整数，但实际开发中 Key 可能是字符串（如 “apple”）、日期（如 2024-05-20）等非整数类型。这时候需要将非整数 Key 转换为整数，再进行哈希计算 —— 这个转换过程通常通过仿函数实现。

字符串 Key 的转换：BKDR 哈希算法

字符串转换为整数的核心要求是：让不同的字符串尽可能映射到不同的整数，避免转换后产生额外冲突。直接将字符的 ASCII 码相加是不可行的（比如 “abcd” 和 “bcad” 的 ASCII 码和相同）。

实战中最常用的是BKDR 哈希算法，它的逻辑是：用一个质数（如 31、131）作为基数，迭代计算字符串的哈希值，让每个字符都参与运算：

hash = hash × 基数 + 当前字符的 ASCII 码

选择 31 作为基数的原因是：31 是质数，且 31 = 2^5 - 1，乘法运算可以被优化为位运算（hash × 31 = hash << 5 - hash），效率更高。

C++ 仿函数实现

下面是 C++ 中字符串 Key 的哈希转换仿函数，同时支持整数 Key 的默认转换：

// 通用哈希仿函数（支持整数Key）
template<class K>
struct HashFunc {size_t operator()(const K& key) {return (size_t)key; // 直接转换为size_t}
};// 字符串Key的特化仿函数（BKDR哈希算法）
template<>
struct HashFunc<string> {size_t operator()(const string& key) {size_t hash = 0;// 基数选择131，让每个字符参与运算for (auto ch : key) {hash = hash * 131 + ch;}return hash;}
};

使用时，哈希表类可以将该仿函数作为模板参数，支持任意可转换为整数的 Key 类型：

template<class K, class V, class Hash = HashFunc<K>>
class HashTable {// 哈希表实现...
};

2.5 其他哈希函数（了解即可）

除了上述方法以外，还有一些适用于特定场景的哈希函数：

平方取中法：将 Key 平方后，取中间几位作为哈希值（适用于 Key 分布均匀的场景）；
折叠法：将 Key 拆分为若干段，将各段相加得到哈希值（适用于 Key 较长的场景，如身份证号）；
数学分析法：根据 Key 的分布规律设计哈希函数（适用于已知 Key 分布的场景）。

这些方法在《数据结构（C 语言版）》（严蔚敏）、《数据结构：用面向对象方法与 C++ 语言描述》（殷人昆）等教材中有详细讲解，大家如果感兴趣的话的可以自行深入研究。

三、哈希冲突解决：当关键字 “撞车” 了怎么办？

无论哈希函数设计得多优秀，冲突都无法完全避免。实战中处理哈希冲突的核心方法有两种：开放定址法和链地址法（拉链法）。其中链地址法因实现简单、性能稳定，被广泛应用于 STL 的 unordered_map、Java 的 HashMap 等容器中。

3.1 开放定址法：在数组内寻找 “空位”

开放定址法的核心逻辑是：所有元素都存储在哈希表的数组中，当某个关键字的哈希位置被占用时，按照某种规则在数组中寻找下一个空位置存储。

它的约束是：负载因子 α 必须小于 1（数组不能满，否则没有空位可找）。常用的寻找规则有三种：线性探测、二次探测、双重探测。

3.1.1 线性探测：依次向后寻找

线性探测是最简单的开放定址法，规则是：

用哈希函数计算初始位置 hash0 = Key % M；
如果 hash0 被占用，依次探测 hash0+1、hash0+2、…，直到找到空位置；
若探测到数组末尾，回绕到数组开头继续探测（循环探测）。

数学表达式为：h_i (Key) = (hash0 + i) % M（i=1,2,...,M-1）

示例演示

假设 M=11（数组下标 0-10），关键字集合 {19,30,5,36,13,20,21,12}：

19%11=8 → 下标 8（空，存储 19）；
30%11=8 → 下标 8（被占用，探测 9→空，存储 30）；
5%11=5 → 下标 5（空，存储 5）；
36%11=3 → 下标 3（空，存储 36）；
13%11=2 → 下标 2（空，存储 13）；
20%11=9 → 下标 9（被占用，探测 10→空，存储 20）；
21%11=10 → 下标 10（被占用，探测 0→空，存储 21）；
12%11=1 → 下标 1（空，存储 12）。

最终数组存储结果（下标 0-10）：21、12、13、36、空、5、空、空、19、30、20。

线性探测的问题：群集（堆积）

线性探测的缺点是很明显的：如果某个区域的位置被连续占用，后续冲突的关键字都会往这个区域聚集，形成 “群集”（比如下标 8、9、10 被占用后，后续映射到这些下标的关键字都会探测下标 0）。群集会导致探测次数增多，查询效率下降。

3.1.2 二次探测：平方跳跃式寻找

二次探测的核心是通过平方数跳跃探测，避免线性探测的群集问题。规则是：

初始位置 hash0 = Key % M；
若 hash0 被占用，依次探测 hash0+1²、hash0-1²、hash0+2²、hash0-2²、…；
探测范围限制在 i ≤ M/2（避免重复探测），若探测到负数或超出数组范围，需调整到 [0, M-1] 区间。

数学表达式为：h_i (Key) = (hash0 ± i²) % M（i=1,2,...,M/2）

示例演示

假设 M=11，关键字集合 {19,30,52,63,11,22}：

19%11=8 → 下标 8（空，存储 19）；
30%11=8 → 探测 8+1²=9（空，存储 30）；
52%11=8 → 探测 8+1²=9（被占用）→ 8-1²=7（空，存储 52）；
63%11=8 → 探测 8+1²=9（被占用）→ 8-1²=7（被占用）→ 8+2²=12→1（空，存储 63）；
11%11=0 → 下标 0（空，存储 11）；
22%11=0 → 探测 0+1²=1（被占用）→ 0-1²=-1→10（空，存储 22）。

二次探测能有效减少群集，但无法完全避免 —— 如果关键字的哈希值分布不均匀，仍可能出现局部群集。

3.1.3 双重探测：用第二个哈希函数计算偏移量

双重探测（也叫双散列）的核心是用第二个哈希函数计算探测的偏移量，让探测路径更分散。规则是：

第一个哈希函数计算初始位置 hash0 = h1 (Key) = Key % M；
第二个哈希函数计算偏移量 step = h2 (Key)（要求 step < M 且与 M 互质）；
若 hash0 被占用，依次探测 hash0+step、hash0+2×step、…，直到找到空位置。

数学表达式为：h_i (Key) = (hash0 + i×h2 (Key)) % M（i=1,2,...,M-1）

关键要求：h2 (Key) 与 M 互质

h2 (Key) 必须与 M 互质（最大公约数为 1），否则探测路径会局限在部分位置，无法遍历整个数组。常用的 h2 (Key) 设计：

当 M 为 2 的整数次幂时，h2 (Key) 取奇数（奇数与 2 的整数次幂互质）；
当 M 为质数时，h2 (Key) = Key % (M-1) + 1（确保 step 在 [1, M-1] 之间，且与 M 互质）。

示例演示

假设 M=11（质数），h2 (Key)=Key%10+1，关键字集合 {19,30,52,74}：

19%11=8 → 下标 8（空，存储 19）；
30%11=8 → step=30%10+1=1 → 探测 8+1=9（空，存储 30）；
52%11=8 → step=52%10+1=3 → 探测 8+3=11→0（空，存储 52）；
74%11=8 → step=74%10+1=5 → 探测 8+5=13→2（空，存储 74）。

双重探测的探测路径最分散，能最大程度避免群集，是开放定址法中性能最优的方案，但实现相对复杂。

3.1.4 开放定址法的删除问题：状态标识

开放定址法的一个关键问题是删除元素不能直接置空—— 如果直接将某个位置置空，后续探测该位置的关键字会误以为 “前面没有冲突元素”，导致查找失败。

比如前面的线性探测示例中，若删除下标 9 的 30，直接将下标 9 置空，后续查找 20 时，探测到下标 9 为空就会停止，无法找到下标 10 的 20。

解决该问题的方案是给每个位置增加状态标识：

EMPTY：初始状态，该位置从未存储过元素；
EXIST：该位置当前存储着元素；
DELETE：该位置的元素已被删除，可重新存储。

查找时，只有遇到 EMPTY 状态才停止探测；删除时，将状态改为 DELETE 而非置空；插入时，可将元素存储到 DELETE 或 EMPTY 状态的位置。

3.2 链地址法（拉链法）：冲突元素 “链表化”

链地址法是实战中最常用的冲突解决机制，STL 的 unordered_map、Java 的 HashMap 都采用这种方式。它的核心逻辑是：

哈希表的底层是一个指针数组（桶数组），每个元素是一个链表的头指针；
用哈希函数计算关键字的桶下标（hash = Key % M）；
若该桶为空，直接将元素作为链表头节点插入；
若该桶已有关键字（冲突），将元素插入到链表的头部或尾部。

简单说，链地址法是将冲突的关键字 “串成链表”，挂在对应的桶下面，因此也叫 “哈希桶”。

示例演示

假设 M=11，关键字集合 {19,30,5,36,13,20,21,12,24,96}：

19%11=8 → 桶 8 链表：19；
30%11=8 → 桶 8 链表：30 → 19；
5%11=5 → 桶 5 链表：5；
36%11=3 → 桶 3 链表：36；
13%11=2 → 桶 2 链表：13；
20%11=9 → 桶 9 链表：20；
21%11=10 → 桶 10 链表：21；
12%11=1 → 桶 1 链表：12；
24%11=2 → 桶 2 链表：24 → 13；
96%11=8 → 桶 8 链表：96 → 30 → 19。

最终桶数组结构如下（下标 0-10）：

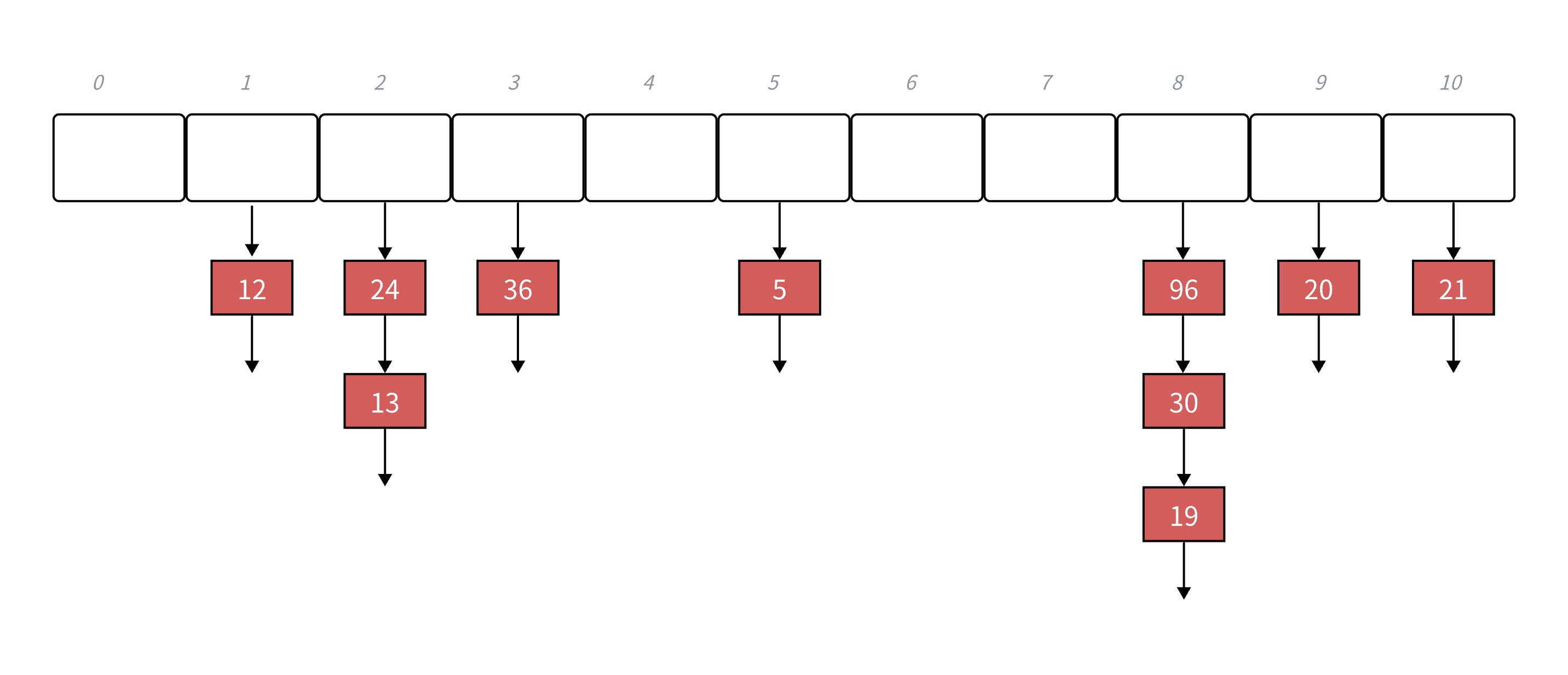
链地址法的优势

相比开放定址法，链地址法有明显优势：

无群集问题：冲突元素只在各自的链表中存储，不影响其他桶；
负载因子可大于 1：链表可以无限延长（理论上），无需严格限制负载因子；
删除简单：直接删除链表节点即可，无需状态标识；
空间利用率高：桶数组可以按需扩容，链表节点只在有冲突时创建。

极端场景优化：链表转红黑树

链地址法的唯一缺点是：如果某个桶的链表过长（比如恶意攻击或关键字分布极端），查询效率会降至 O (n)。为了解决这个问题，Java 8 的 HashMap 引入了优化：当链表长度超过阈值（默认 8）时，将链表转换为红黑树，查询效率提升至 O (log n)。

STL 的 unordered_map 没有这个优化，因为它假设哈希函数足够优秀，链表过长的场景极少发生。实际开发中，只要哈希函数设计合理，无需额外处理。

四、C++ 实现开放定址法哈希表（线性探测）

前面讲解了开放定址法的原理，下面基于 C++ 实现一个采用线性探测的哈希表，支持增删查改、扩容、非整数 Key 等核心功能。

4.1 设计思路

底层存储：用 vector 存储哈希节点，每个节点包含键值对和状态标识；
哈希函数：通过仿函数实现，支持整数和字符串 Key；
冲突解决：采用线性探测；
扩容策略：负载因子≥0.7 时扩容，扩容后数组大小为下一个质数（参考 SGI STL 的质数表）；
状态标识：EMPTY、EXIST、DELETE，解决删除问题。

4.2 完整代码实现

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;// 哈希仿函数：支持整数Key
template<class K>
struct HashFunc {size_t operator()(const K& key) {return (size_t)key;}
};// 字符串Key的特化仿函数（BKDR哈希）
template<>
struct HashFunc<string> {size_t operator()(const string& key) {size_t hash = 0;for (auto ch : key) {hash = hash * 131 + ch; // 131为基数，兼顾效率和分布性}return hash;}
};namespace open_address {// 节点状态标识enum State {EMPTY,   // 空状态（从未存储）EXIST,   // 存在元素DELETE   // 已删除};// 哈希节点结构template<class K, class V>struct HashData {pair<K, V> _kv;     // 键值对State _state = EMPTY; // 状态，默认空};// 开放定址法哈希表（线性探测）template<class K, class V, class Hash = HashFunc<K>>class HashTable {private:vector<HashData<K, V>> _tables; // 底层存储数组size_t _n = 0;                  // 存储的元素个数// 质数表：参考SGI STL，用于扩容时获取下一个质数static const unsigned long __stl_prime_list[];static const int __stl_num_primes;// 获取大于等于n的最小质数（用于扩容）unsigned long __stl_next_prime(unsigned long n) {const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;// 二分查找第一个大于等于n的质数const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}public:// 构造函数：初始化数组大小为第一个质数（53）HashTable() {_tables.resize(__stl_next_prime(0));}// 插入键值对：成功返回true，已存在返回falsebool Insert(const pair<K, V>& kv) {// 先查找，若已存在则返回falseif (Find(kv.first) != nullptr) {return false;}// 负载因子≥0.7，扩容if (_n * 10 / _tables.size() >= 7) {// 创建新哈希表，大小为当前的下一个质数HashTable<K, V, Hash> newHT;newHT._tables.resize(__stl_next_prime(_tables.size() + 1));// 将旧表中的元素插入新表（重新哈希）for (size_t i = 0; i < _tables.size(); ++i) {if (_tables[i]._state == EXIST) {newHT.Insert(_tables[i]._kv);}}// 交换新旧表的底层数组（现代C++深拷贝优化）_tables.swap(newHT._tables);}Hash hash;size_t hash0 = hash(kv.first) % _tables.size(); // 初始哈希位置size_t hashi = hash0;size_t i = 1;// 线性探测：寻找空位置（EMPTY或DELETE）while (_tables[hashi]._state == EXIST) {hashi = (hash0 + i) % _tables.size(); // 循环探测++i;}// 插入元素，更新状态和元素个数_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;}// 查找Key：存在返回节点指针，否则返回nullptrHashData<K, V>* Find(const K& key) {Hash hash;size_t hash0 = hash(key) % _tables.size();size_t hashi = hash0;size_t i = 1;// 探测直到遇到EMPTY（停止）或找到EXIST且Key匹配while (_tables[hashi]._state != EMPTY) {if (_tables[hashi]._state == EXIST && _tables[hashi]._kv.first == key) {return &_tables[hashi];}// 线性探测下一个位置hashi = (hash0 + i) % _tables.size();++i;// 防止死循环（理论上负载因子<1，不会出现）if (i > _tables.size()) {break;}}return nullptr;}// 删除Key：成功返回true，不存在返回falsebool Erase(const K& key) {HashData<K, V>* ret = Find(key);if (ret == nullptr) {return false;}// 标记为DELETE，不直接删除数据ret->_state = DELETE;--_n;return true;}// 获取元素个数size_t Size() const {return _n;}// 判空bool Empty() const {return _n == 0;}// 打印哈希表（调试用）void Print() {for (size_t i = 0; i < _tables.size(); ++i) {if (_tables[i]._state == EXIST) {cout << "下标" << i << ": " << _tables[i]._kv.first << " → " << _tables[i]._kv.second << endl;} else if (_tables[i]._state == DELETE) {cout << "下标" << i << ": [已删除]" << endl;} else {cout << "下标" << i << ": [空]" << endl;}}cout << "当前元素个数：" << _n << endl;cout << "当前负载因子：" << (double)_n / _tables.size() << endl;}};// 初始化质数表template<class K, class V, class Hash>const unsigned long HashTable<K, V, Hash>::__stl_prime_list[] = {53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};template<class K, class V, class Hash>const int HashTable<K, V, Hash>::__stl_num_primes = sizeof(__stl_prime_list) / sizeof(__stl_prime_list[0]);
}// 测试代码
int main() {open_address::HashTable<string, int> ht;// 插入测试ht.Insert({"apple", 10});ht.Insert({"banana", 20});ht.Insert({"orange", 30});ht.Insert({"grape", 40});ht.Insert({"pear", 50});cout << "插入后哈希表：" << endl;ht.Print();cout << endl;// 查找测试auto apple = ht.Find("apple");if (apple) {cout << "查找apple：" << apple->_kv.first << " → " << apple->_kv.second << endl;} else {cout << "查找apple：未找到" << endl;}auto mango = ht.Find("mango");if (mango) {cout << "查找mango：" << mango->_kv.first << " → " << mango->_kv.second << endl;} else {cout << "查找mango：未找到" << endl;}cout << endl;// 删除测试bool ret = ht.Erase("banana");cout << "删除banana：" << (ret ? "成功" : "失败") << endl;cout << "删除后哈希表：" << endl;ht.Print();cout << endl;// 插入已删除的Keyret = ht.Insert({"banana", 25});cout << "重新插入banana：" << (ret ? "成功" : "失败") << endl;cout << "重新插入后哈希表：" << endl;ht.Print();return 0;
}

4.3 代码解析

哈希节点结构：每个节点包含键值对（pair<K,V>）和状态标识（State），解决删除问题；
质数表：参考 SGI STL 的实现，扩容时选择下一个质数作为新数组大小，保证哈希分布均匀；
扩容逻辑：负载因子≥0.7 时，创建新哈希表，将旧表元素重新哈希插入新表，通过 swap 交换底层数组，避免深拷贝的性能开销；
插入逻辑：先查找是否存在，再判断是否扩容，最后通过线性探测找到空位置插入；
查找逻辑：线性探测直到遇到 EMPTY 状态，或找到匹配的 Key；
删除逻辑：将节点状态改为 DELETE，而非直接删除数据，不影响后续查找。

五、C++ 实现链地址法哈希表（哈希桶）

链地址法是实战中更常用的实现方式，下面基于 C++ 实现一个哈希桶，支持增删查改、高效扩容、非整数 Key 等功能。

5.1 设计思路

底层存储：用 vector 存储链表头指针（桶数组），每个桶对应一个链表；
哈希节点：链表节点包含键值对和下一个节点的指针；
哈希函数：复用前面的 HashFunc 仿函数；
扩容策略：负载因子≥1 时扩容，扩容后数组大小为下一个质数；
冲突解决：冲突元素插入到对应桶的链表头部（头插效率高）。

5.2 完整代码实现

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;// 哈希仿函数：支持整数Key
template<class K>
struct HashFunc {size_t operator()(const K& key) {return (size_t)key;}
};// 字符串Key的特化仿函数（BKDR哈希）
template<>
struct HashFunc<string> {size_t operator()(const string& key) {size_t hash = 0;for (auto ch : key) {hash = hash * 131 + ch;}return hash;}
};namespace hash_bucket {// 哈希链表节点template<class K, class V>struct HashNode {pair<K, V> _kv;         // 键值对HashNode<K, V>* _next;  // 下一个节点指针// 构造函数HashNode(const pair<K, V>& kv): _kv(kv), _next(nullptr) {}};// 链地址法哈希表（哈希桶）template<class K, class V, class Hash = HashFunc<K>>class HashTable {private:typedef HashNode<K, V> Node;vector<Node*> _tables; // 桶数组（存储链表头指针）size_t _n = 0;         // 存储的元素个数// 质数表：用于扩容static const unsigned long __stl_prime_list[];static const int __stl_num_primes;// 获取下一个质数unsigned long __stl_next_prime(unsigned long n) {const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}public:// 构造函数：初始化桶数组为第一个质数（53），所有桶为空指针HashTable() {_tables.resize(__stl_next_prime(0), nullptr);}// 析构函数：释放所有节点和桶数组~HashTable() {// 遍历每个桶，释放链表节点for (size_t i = 0; i < _tables.size(); ++i) {Node* cur = _tables[i];while (cur) {Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr; // 桶置空}}// 插入键值对：头插法，效率O(1)bool Insert(const pair<K, V>& kv) {// 查找是否已存在，避免重复插入if (Find(kv.first) != nullptr) {return false;}// 负载因子≥1，扩容if (_n == _tables.size()) {// 新桶数组大小为下一个质数size_t newSize = __stl_next_prime(_tables.size() + 1);vector<Node*> newTables(newSize, nullptr);Hash hash;// 遍历旧桶，将节点重新映射到新桶for (size_t i = 0; i < _tables.size(); ++i) {Node* cur = _tables[i];while (cur) {Node* next = cur->_next; // 保存下一个节点// 计算节点在新桶中的位置size_t hashi = hash(cur->_kv.first) % newTables.size();// 头插法插入新桶cur->_next = newTables[hashi];newTables[hashi] = cur;cur = next; // 处理下一个节点}_tables[i] = nullptr; // 旧桶置空}// 交换新旧桶数组_tables.swap(newTables);}Hash hash;size_t hashi = hash(kv.first) % _tables.size(); // 计算桶下标// 头插法插入新节点Node* newNode = new Node(kv);newNode->_next = _tables[hashi];_tables[hashi] = newNode;++_n;return true;}// 查找Key：返回节点指针，不存在返回nullptrNode* Find(const K& key) {Hash hash;size_t hashi = hash(key) % _tables.size(); // 找到对应的桶Node* cur = _tables[hashi];// 遍历链表查找while (cur) {if (cur->_kv.first == key) {return cur;}cur = cur->_next;}return nullptr;}// 删除Key：成功返回true，不存在返回falsebool Erase(const K& key) {Hash hash;size_t hashi = hash(key) % _tables.size(); // 找到对应的桶Node* prev = nullptr;Node* cur = _tables[hashi];// 遍历链表查找要删除的节点while (cur) {if (cur->_kv.first == key) {// 找到节点，删除if (prev == nullptr) {// 要删除的是头节点，更新桶的头指针_tables[hashi] = cur->_next;} else {// 要删除的是中间节点， prev->next指向cur->nextprev->_next = cur->_next;}delete cur;--_n;return true;}// 移动指针prev = cur;cur = cur->_next;}return false;}// 获取元素个数size_t Size() const {return _n;}// 判空bool Empty() const {return _n == 0;}// 打印哈希表（调试用）void Print() {for (size_t i = 0; i < _tables.size(); ++i) {cout << "桶" << i << ": ";Node* cur = _tables[i];while (cur) {cout << cur->_kv.first << "→" << cur->_kv.second << " ";cur = cur->_next;}cout << endl;}cout << "当前元素个数：" << _n << endl;cout << "当前负载因子：" << (double)_n / _tables.size() << endl;}// 禁止拷贝构造和赋值（简化实现，如需支持可自行添加深拷贝）HashTable(const HashTable&) = delete;HashTable& operator=(const HashTable&) = delete;};// 初始化质数表template<class K, class V, class Hash>const unsigned long HashTable<K, V, Hash>::__stl_prime_list[] = {53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};template<class K, class V, class Hash>const int HashTable<K, V, Hash>::__stl_num_primes = sizeof(__stl_prime_list) / sizeof(__stl_prime_list[0]);
}// 测试代码
int main() {hash_bucket::HashTable<string, int> ht;// 插入测试ht.Insert({"apple", 10});ht.Insert({"banana", 20});ht.Insert({"orange", 30});ht.Insert({"grape", 40});ht.Insert({"pear", 50});ht.Insert({"watermelon", 60});ht.Insert({"pineapple", 70});cout << "插入后哈希表：" << endl;ht.Print();cout << endl;// 查找测试auto orange = ht.Find("orange");if (orange) {cout << "查找orange：" << orange->_kv.first << " → " << orange->_kv.second << endl;} else {cout << "查找orange：未找到" << endl;}auto peach = ht.Find("peach");if (peach) {cout << "查找peach：" << peach->_kv.first << " → " << peach->_kv.second << endl;} else {cout << "查找peach：未找到" << endl;}cout << endl;// 删除测试bool ret = ht.Erase("grape");cout << "删除grape：" << (ret ? "成功" : "失败") << endl;cout << "删除后哈希表：" << endl;ht.Print();cout << endl;// 插入重复Keyret = ht.Insert({"apple", 15});cout << "插入重复的apple：" << (ret ? "成功" : "失败") << endl;cout << "最终哈希表：" << endl;ht.Print();return 0;
}

5.3 代码解析

哈希节点：采用链表节点结构，包含键值对和下一个节点指针，支持链式存储；
桶数组：vector<Node*> 存储每个链表的头指针，初始时所有桶为空指针；
扩容逻辑：负载因子≥1 时扩容，新桶数组大小为下一个质数。扩容时无需重新创建节点，只需将旧桶的节点重新映射到新桶并调整指针，效率更高；
插入逻辑：头插法插入新节点，时间复杂度 O (1)，无需探测空位置；
查找逻辑：遍历对应桶的链表，时间复杂度取决于链表长度（平均 O (1)）；
删除逻辑：找到要删除的节点，调整前后节点的指针，释放节点内存，无需状态标识；
析构函数：遍历所有桶，释放每个链表的节点，避免内存泄漏。