数据结构——四十二、二叉排序树(王道408)
文章目录
- 前言
- 一.二叉排序树的定义
- 二.二叉排序树的查找
- 1.思路
- 2.代码
- 3.使用过程
- 三.二叉排序树的插入
- 1.思路
- 2.代码
- 3.使用过程
- 四.二叉排序树的构造
- 1.思路
- 2.代码
- 3.使用过程
- 五.二叉排序树的删除
- 1.思路
- 六.查找效率分析
- 1.查找成功
- 1.计算平均查找长度(ASL)
- 2.查找的时间复杂度
- 2.查找失败
- 1.计算平均查找长度(ASL)
- 七.知识回顾与重要考点
- 结语
前言
本文介绍了二叉排序树(BST)的定义、查找、插入、构造和删除操作。二叉排序树是一种左子树结点值小于根结点值,右子树结点值大于根结点值的特殊二叉树,其中序遍历可得到递增序列。查找操作通过比较关键字值在左右子树中递归搜索。插入操作根据关键字大小决定插入位置。构造BST即不断插入新结点的过程。删除操作需分三种情况处理:删除叶子结点、仅有一棵子树的结点或两棵子树的结点。对于同时有左右子树的结点,可采用直接后继代替法处理。文章通过图示和代码示例详细说明了各操作的实现过程和应用场景。
一.二叉排序树的定义
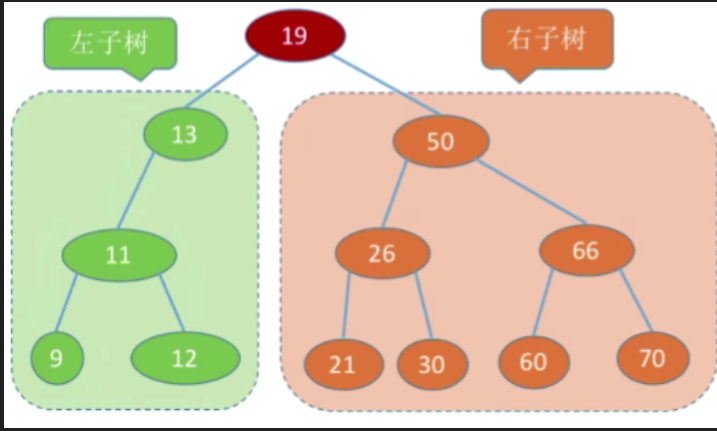
- 二叉排序树,又称二叉查找树(BST). Binary Search Tree)
- 一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。
左子树结点值 < 根结点值 < 右子树结点值
进行中序遍历,可以得到一个递增的有序序列
二叉排序树可用于元素的有序组织、搜索
二.二叉排序树的查找
1.思路
- 若树非空,目标值与根结点的值比较:
- 若相等,则查找成功;
- 若小于根结点,则在左子树上查找,否则在右子树上查找。
- 查找成功,返回结点指针;查找失败返回NULL
2.代码
//二叉排序树结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode,*BSTree;//在二叉排序树中查找值为 key 的结点
BSTNode *BST_Search(BSTree T,int key){while(T!=NULL&&key!=T->key){//若树空或等于根结点值,则结束循环if(key<T->key) T=T->lchild;//小于,则在左子树上查找else T=T->rchild;//大于,则在右子树上查找}return T;
}//在二叉排序树中查找值为 key 的结点(递归实现)
BSTNode *BSTSearch(BSTree T,int key){if (T==NULL)return NULL;//查找失败if (key==T->key)return T;//查找成功else if (key<T->key)return BSTSearch(T->lchild, key); //在左子树中找elsereturn BSTSearch(T->rchild, key); //在右子树中找
}
- 循环迭代算法空间复杂度:O(1)
- 递归空间复杂度:O(h),h为树的高度
3.使用过程
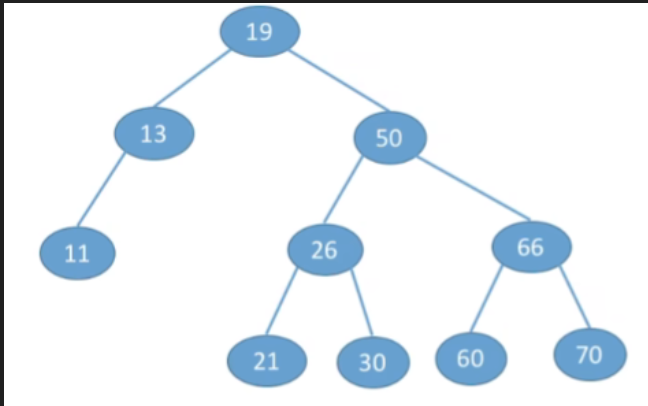
- 查找关键字为30的结点
- 从根节点出发,如果当前访问的节点是一个非空节点,并且我们要找到那个值是要大于当前节点的,那么根据排序数的特性,我们要找的点肯定是在右子树中,所以我们可以让指针往他的右孩子方向走
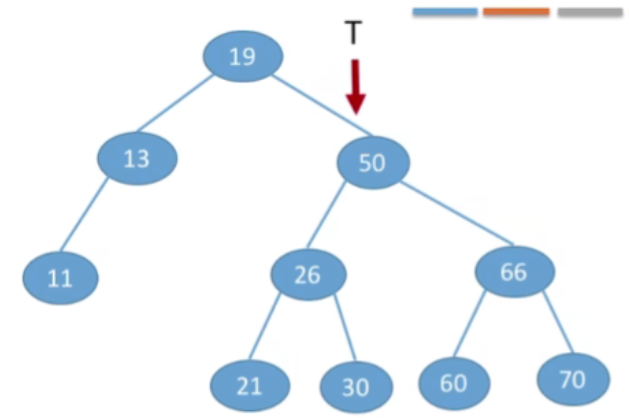
- 现在我们要查找的节点30要比50更小,那肯定是在50这个节点的左子树上,所以就可以往左走
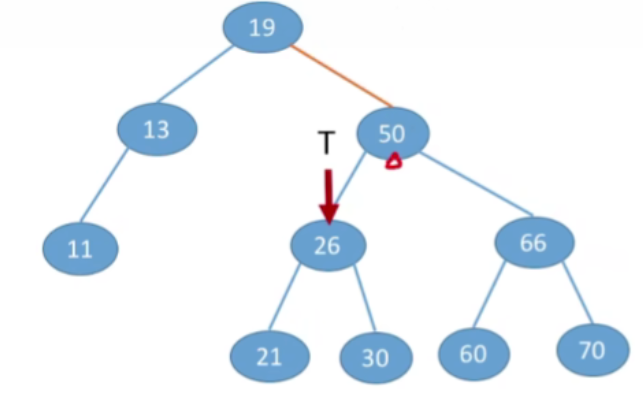
- 接下来的操作类似,结果如下:
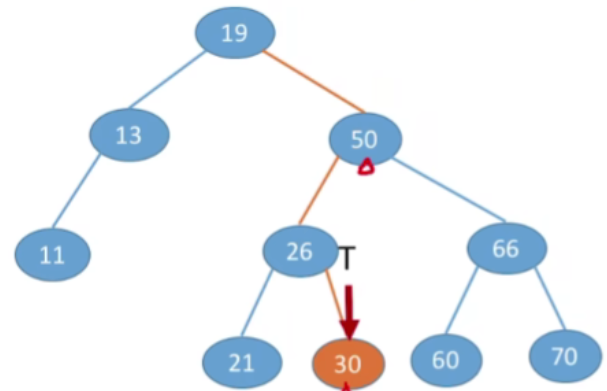
- 假设此时T指向的是NULL,说明查找失败
三.二叉排序树的插入
1.思路
- 若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树
2.代码
//在二叉排序树插入关键字为k的新结点(递归实现)
int BST_INSERT(BSTree&T, int k){if(T==NULL){ //原树为空,新插入的结点为根结点T=(BSTree)malloc(sizeof(BSTNode));T->key=k;T->lchild=T->rchild=NULL;return 1; //返回1,插入成功}else if(k==T->key) //树中存在相同关键字的结点,插入失败return 0;else if(k<T->key) //插入到T的左子树return BST_INSERT(T->lchild,k);else //插入到T的右子树return BST_INSERT(T->rchild,k);
}// 非递归插入新结点到二叉排序树
bool InsertBST(BSTree *T, int key) {// 创建新结点BSTNode *newNode = (BSTNode *)malloc(sizeof(BSTNode));if (newNode == NULL) {return false; // 内存分配失败}newNode->key = key;newNode->lchild = newNode->rchild = NULL;// 如果树为空,新结点作为根结点if (*T == NULL) {*T = newNode;return true;}BSTNode *current = *T;BSTNode *parent = NULL;// 寻找插入位置while (current != NULL) {parent = current;if (key == current->key) {free(newNode); // 键值已存在,释放新结点return false; // 插入失败} else if (key < current->key) {current = current->lchild; // 在左子树中查找} else {current = current->rchild; // 在右子树中查找}}// 插入新结点if (key < parent->key) {parent->lchild = newNode;} else {parent->rchild = newNode;}return true;
}
- 递归方式最坏空间复杂度O(h),h为树的高度
- 非递归方式空间复杂度为O(1)
3.使用过程
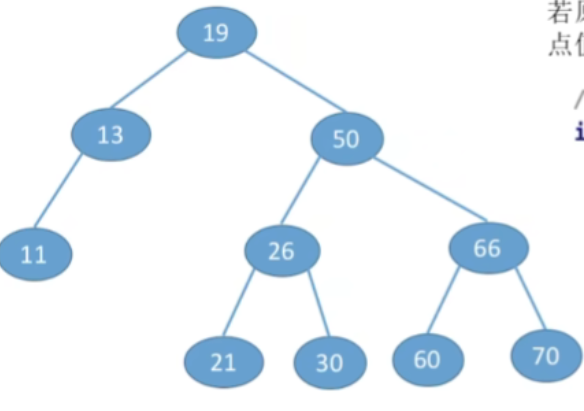
- 插入关键字为12的结点
- 那么从根节点出发,12比19更小,那显然应该插入到左子树
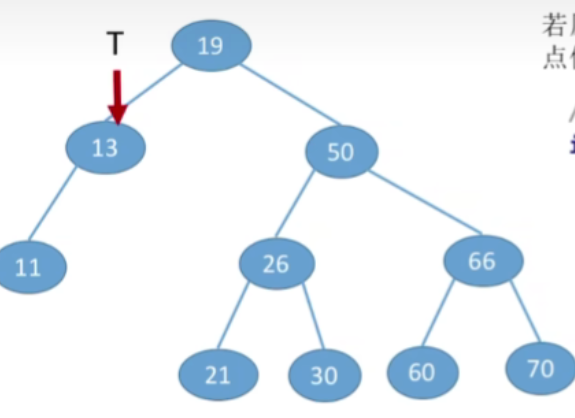
- 接下来12小于13,所以还应该插入到它的左子树当中
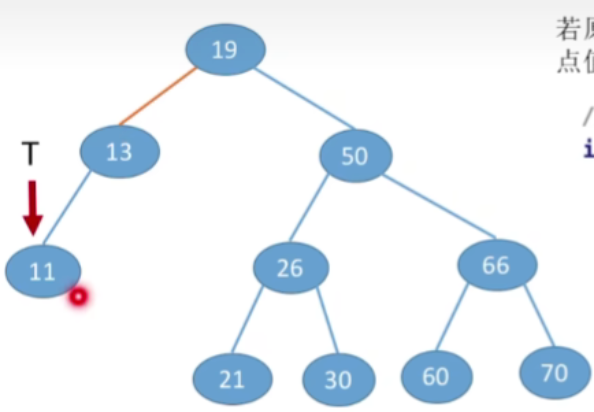
- 那现在12大于11,所以应该插入到当前节点的右子树当中
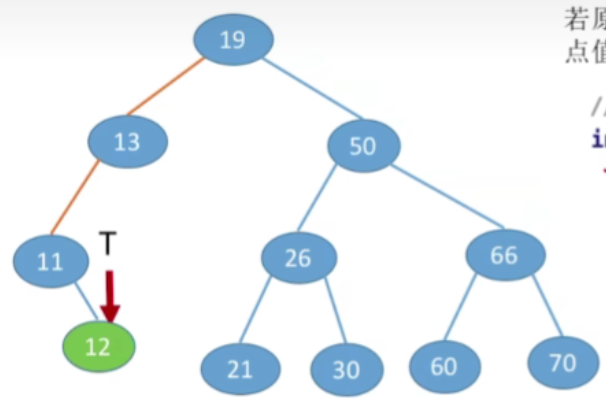
- 如果二叉树中已经有关键字为12的元素,则插入失败
新插入的结点一定是叶子节点
四.二叉排序树的构造
1.思路
- 就是不断插入新结点的过程
2.代码
//按照 str[]中的关键字序列建立二叉排序树
void Creat_BST(BST&T, int str[], int n){T=NULL; //初始时T为空树int i=0;while(i<n){//依次将每个关键字插入到二叉排序树中BST Insert(T,str[i]);i++;}
}
3.使用过程
- 例1: 按照序列str={50,66,60,26,21,30,70,68}建立BST
- 首先插入的是50
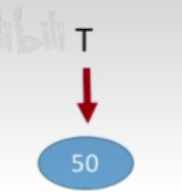
- 接下来66>50,插入到右孩子
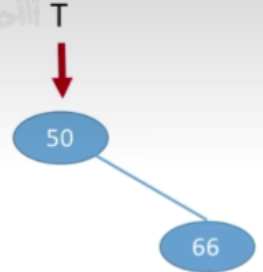
- 60<60应该插在66的左边
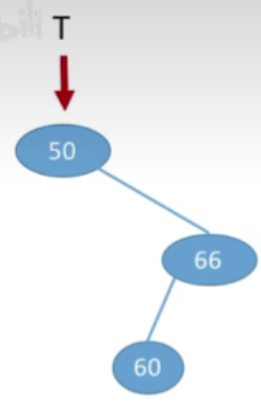
- 然后是26<50,插在50的左孩子
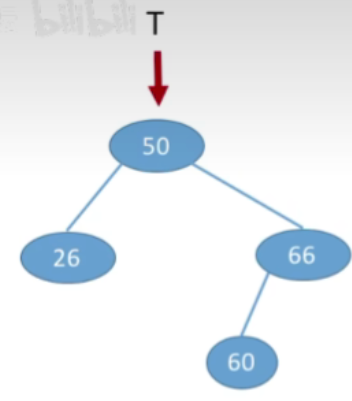
- 接下来操作一样,最终结果如下:
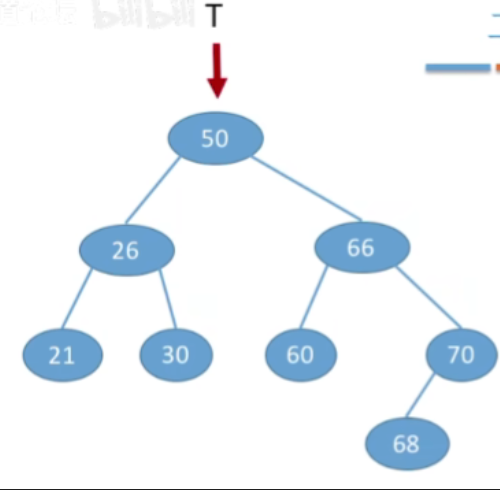
- 例2:按照序列str={50,26,21,30,66,60,70,68}建立BST
- 也是一样的,这里就不展示过程了,直接看结果
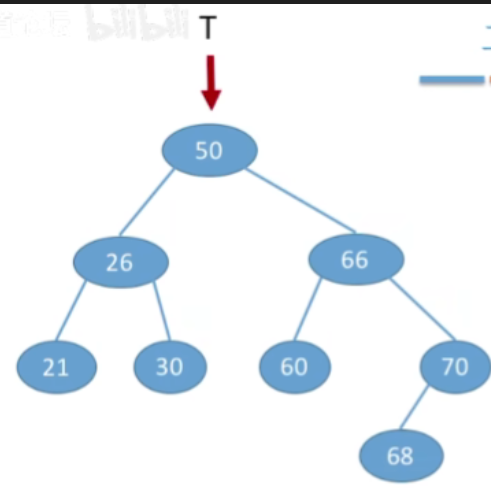
不同的关键字序列可能得到同款二叉排序树
五.二叉排序树的删除
1.思路
- 先搜索找到目标结点:
①若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
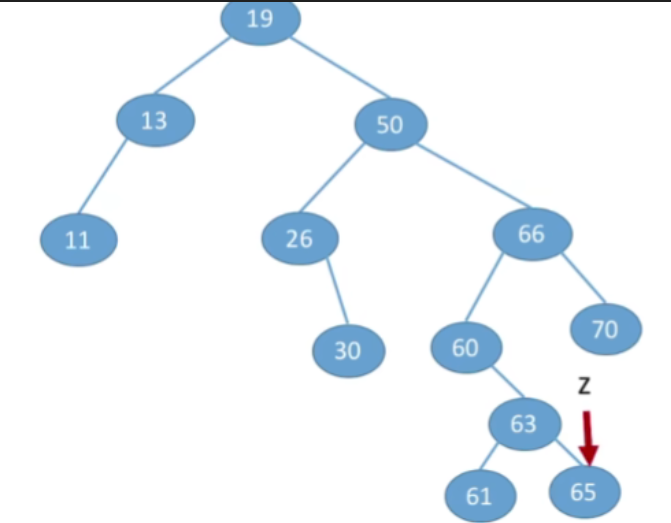
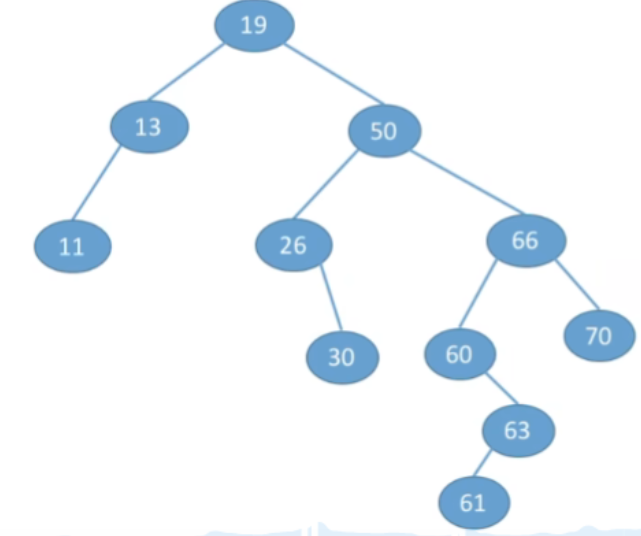
②若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置。
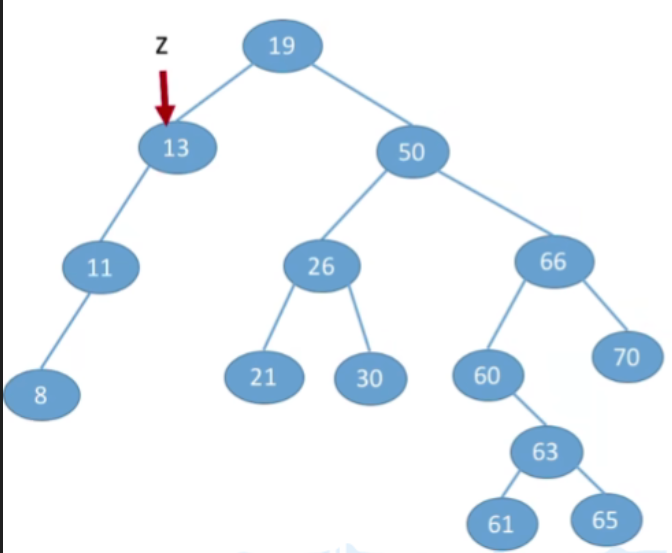
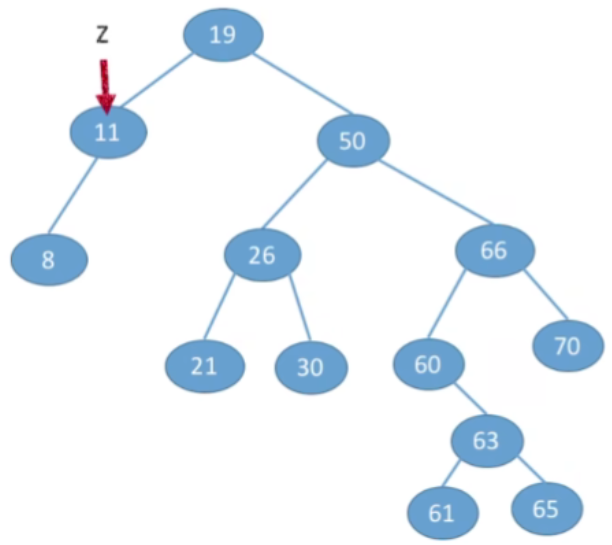
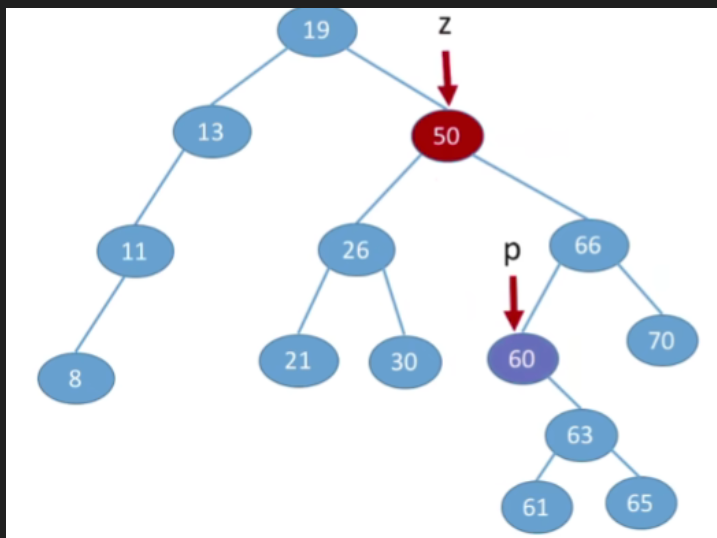
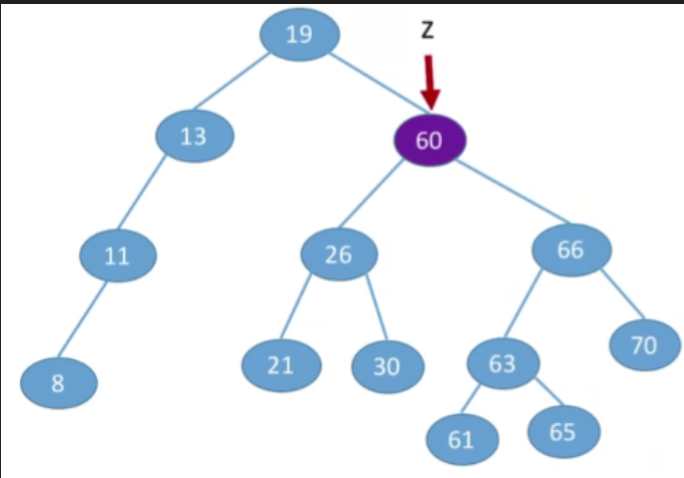
③若结点z有左、右两棵子树,- 第一种方案(直接后继代替法)我们可以从当前删除的节点,它的右子树当中找到值最小的节点(右子树中中序遍历的第一个结点,在树上面看就时左子树中最左下的那个节点),用那个节点来替代当前被删除的节点
- 由于p所指向的结点一定是最左下的结点,因此其一定没有左子树,这样就转换成了我们之前的第二/一种情况
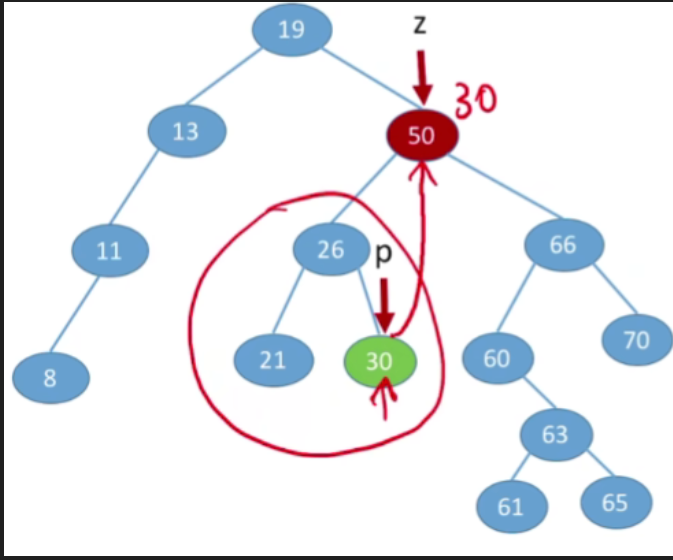
- 第二种方案(直接前驱替代法),找到当前节点它的左子树当中最大的那个值(左子树中最右下的结点),用左子树当中最大的值来替代当前被删除的节点.和之前类似的,p所指向的结点一定没有右子树,则可以转换为之前的第一/二种情况
六.查找效率分析
1.查找成功
1.计算平均查找长度(ASL)
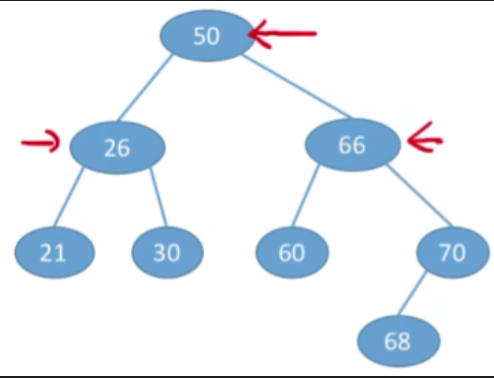
- ASL=(1∗1+2∗2+3∗4+4∗1)/8=2.625ASL=(1*1+2*2+3*4+4*1)/8=2.625ASL=(1∗1+2∗2+3∗4+4∗1)/8=2.625
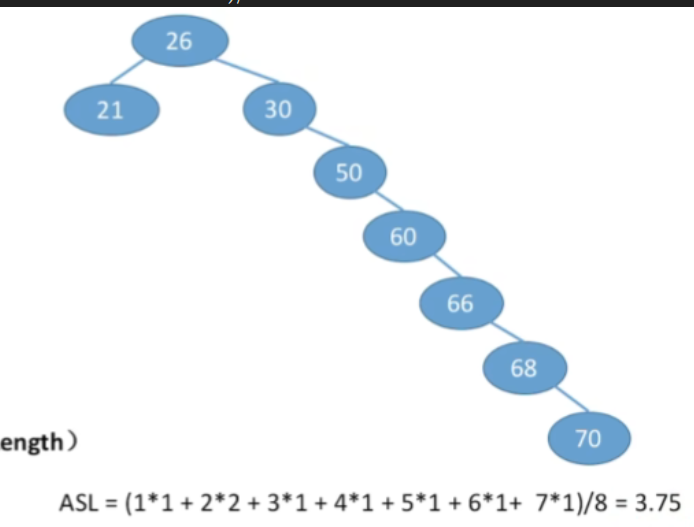
- ASL=(1∗1+2∗2+3∗1+4∗1+5∗1+6∗1+7∗1)/8=3.75ASL = (1*1 + 2*2 + 3*1 + 4*1 + 5*1 + 6*1+ 7*1)/8 = 3.75ASL=(1∗1+2∗2+3∗1+4∗1+5∗1+6∗1+7∗1)/8=3.75
2.查找的时间复杂度
- 最好情况:n个结点的二叉树最小高度为⌊log2n⌋+1\lfloor\log_{2}n\rfloor+1⌊log2n⌋+1。平均查找长度=O(log2n)O(log_{2}n)O(log2n)
- 最坏情况:每个结点只有一个分支,树高h=结点数n。平均查找长度=O(n)
2.查找失败
1.计算平均查找长度(ASL)
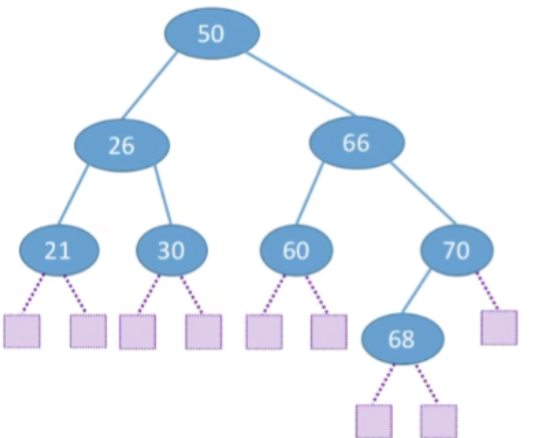
- ASL=(3∗7+4∗2)/9=3.22ASL=(3*7+4*2)/9=3.22ASL=(3∗7+4∗2)/9=3.22
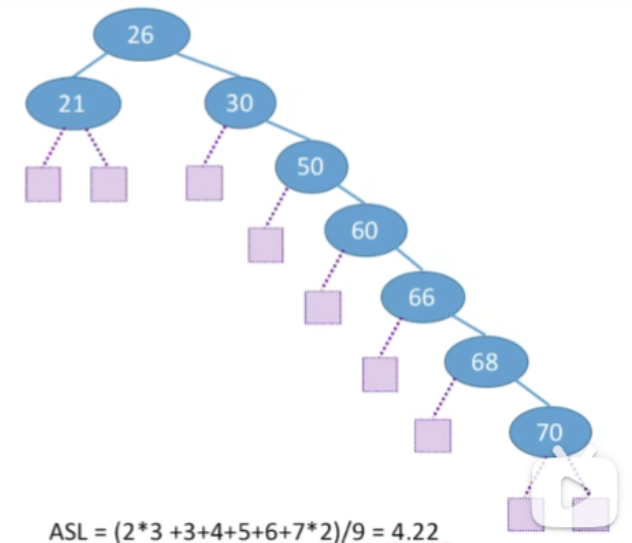
- ASL=(2∗3+3+4+5+6+7∗2)/9=4.22ASL=(2*3+3+4+5+6+7*2)/9=4.22ASL=(2∗3+3+4+5+6+7∗2)/9=4.22
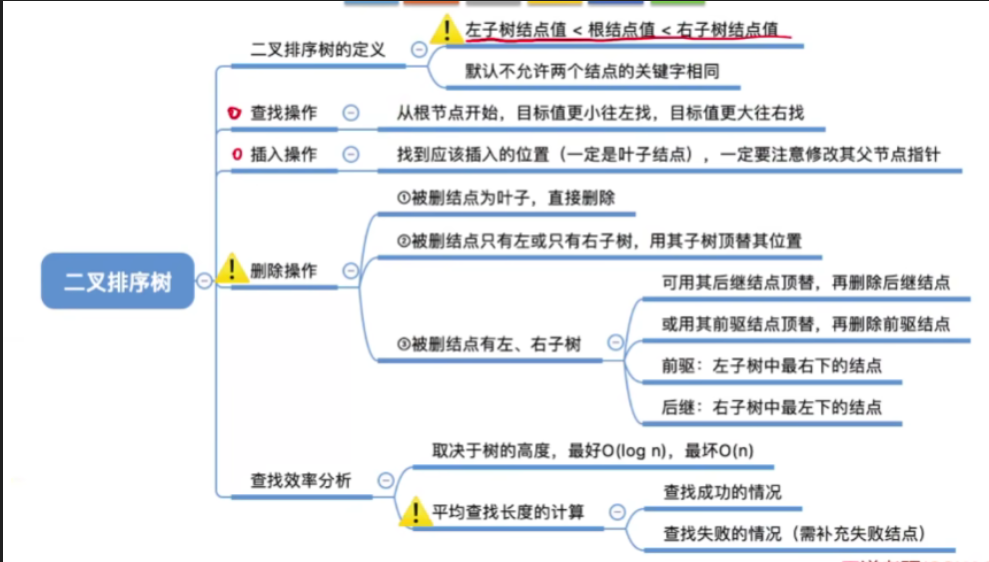
七.知识回顾与重要考点
结语
二更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页
