232. 用栈实现队列
目录
题目链接:
题目:
解题思路:
代码:
问题:
总结:
题目链接:
232. 用栈实现队列 - 力扣(LeetCode)
题目:
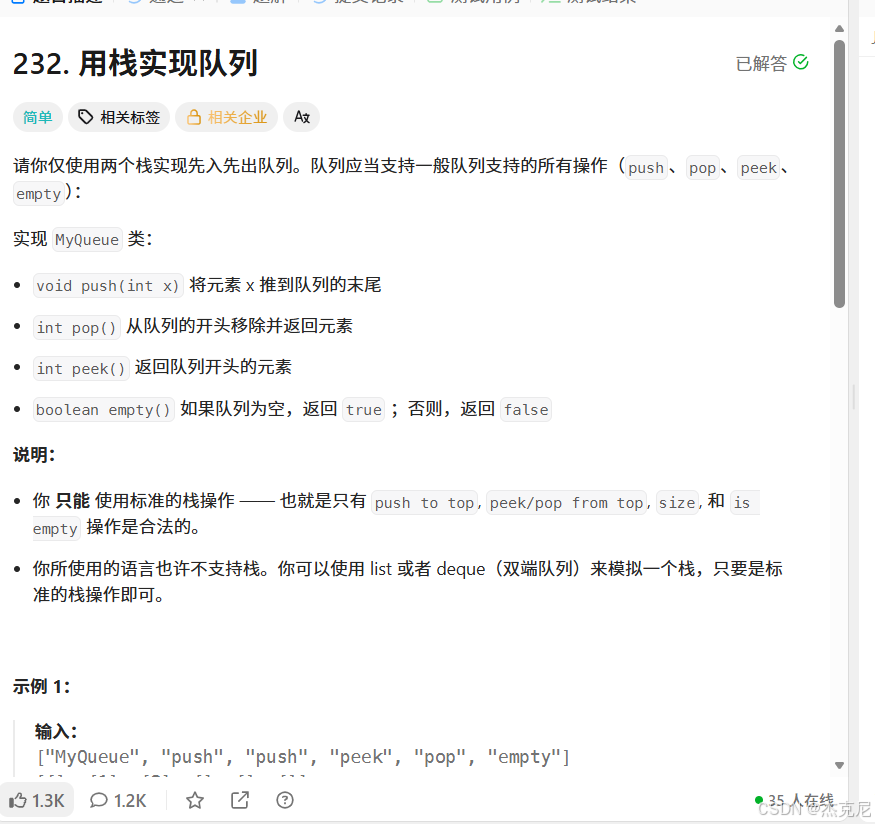
解题思路:
使用两个栈,一个值入栈时,当第一栈空,直接入,当第一栈不空,一直往第二栈放,出栈时,判断出栈顶之后第一栈是否为空,若空,直接将第二栈里面的所有元素放到第一栈里面,判断是否为空的话,第一栈第二栈都要进行判断,获取栈顶元素就是第一栈的栈顶元素,直接使用peek就行
代码:
class MyQueue {Stack<Integer> st1;Stack<Integer> st2;public MyQueue() {st1=new Stack<>();st2=new Stack<>();}public void push(int x) {if(st2.isEmpty()){st2.push(x);return ;}st1.push(x);}public int pop() {int x=st2.pop();if(st2.isEmpty()){while(!st1.isEmpty()){st2.push(st1.pop());}}return x;}public int peek() {return st2.peek();}public boolean empty() {if(st1.isEmpty()&&st2.isEmpty()){return true;}return false;}
}/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = new MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* boolean param_4 = obj.empty();*/问题:
对于Java中栈和队列这里接口和实现类不是特别清楚,想在这里总结弄清楚
栈(先进后出)
Stack<Object> st=new Stack<>();
常用方法
入栈: add()
出栈: pop()
获取栈顶元素;peek()
判断是否为空: isEmpty()
队列(先进先出)
Queue<Object> que=new LinkedList<>();
常用方法:
入队:add()
出队:poll()
获取队头元素:peek()
判断是否为空 isEmpty();
总结:
上面看懂下面不用看
用两个栈实现队列:LeetCode 232 题深度解析与原理探究队列是 “先进先出”(FIFO)的线性数据结构,栈是 “后进先出”(LIFO)的线性数据结构。用两个栈实现队列,是算法领域经典的 “数据结构转换” 问题,也是 LeetCode 232 题的核心考点。本文将从原理、代码实现、复杂度分析、拓展思考四个维度,带你彻底吃透这个问题。一、问题本质与解题思路1. 队列与栈的特性差异队列:元素从队尾(push)进入,从队头(pop)离开,遵循 “先进先出”。例如排队买票,先到的人先买。栈:元素从栈顶(push)进入,也从栈顶(pop)离开,遵循 “后进先出”。例如叠盘子,最后叠的盘子最先被拿走。要实现 “用栈模拟队列”,核心是利用两个栈的 “翻转” 特性:把一个栈作为 “输入栈”(负责接收新元素),另一个栈作为 “输出栈”(负责弹出元素)。当输出栈为空时,将输入栈的所有元素一次性倒入输出栈,此时元素的顺序就会被翻转为 “先进先出”,从而模拟队列的行为。2. 核心操作流程push 操作:优先将元素压入 “输入栈(st1)”;若 “输出栈(st2)” 为空且需要初始化队头元素,可特殊处理(后文代码会详解)。pop 操作:优先从 “输出栈(st2)” 弹出元素;若输出栈为空,先将输入栈的所有元素倒入输出栈,再弹出栈顶元素。peek 操作:与 pop 逻辑类似,只是不弹出元素,仅查看输出栈的栈顶。empty 操作:当两个栈都为空时,队列为空。二、代码实现与逐行解析我们先看完整代码,再逐部分拆解:java运行class MyQueue {
Stack<Integer> st1; // 输入栈:负责接收新元素
Stack<Integer> st2; // 输出栈:负责弹出元素
public MyQueue() {
st1 = new Stack<>();
st2 = new Stack<>();
}
public void push(int x) {
if (st2.isEmpty()) {
st2.push(x);
return;
}
st1.push(x);
}
public int pop() {
int x = st2.pop();
if (st2.isEmpty()) {
while (!st1.isEmpty()) {
st2.push(st1.pop());
}
}
return x;
}
public int peek() {
return st2.peek();
}
public boolean empty() {
return st1.isEmpty() && st2.isEmpty();
}
}
1. 类与成员变量定义java运行class MyQueue {
Stack<Integer> st1;
Stack<Integer> st2;
定义两个栈 st1 和 st2,分别承担 “输入栈” 和 “输出栈” 的角色。st1 负责接收新元素(模拟队列的 “入队” 操作);st2 负责弹出元素(模拟队列的 “出队” 操作)。2. 构造方法:初始化两个栈java运行public MyQueue() {
st1 = new Stack<>();
st2 = new Stack<>();
}
构造方法中,为 st1 和 st2 分别实例化 Stack 对象,完成初始状态的初始化。3. push 方法:元素入队java运行public void push(int x) {
if (st2.isEmpty()) {
st2.push(x);
return;
}
st1.push(x);
}
逻辑:如果 st2 为空,说明当前没有 “待弹出” 的元素,此时将新元素直接压入 st2(作为队头的初始元素);否则,将新元素压入 st1(作为后续待翻转的元素)。这样设计的目的是保证 st2 的栈顶始终是 “最早进入队列” 的元素(即队头),从而让 pop 和 peek 操作可以直接从 st2 处理。4. pop 方法:元素出队java运行public int pop() {
int x = st2.pop(); // 先弹出st2的栈顶(队头元素)
if (st2.isEmpty()) { // 若st2为空,将st1的所有元素倒入st2
while (!st1.isEmpty()) {
st2.push(st1.pop());
}
}
return x;
}
第一步:直接弹出 st2 的栈顶元素,这是当前队列的队头元素(因为 st2 存储的是 “翻转后” 的元素,栈顶就是最早进入的元素)。第二步:若 st2 为空,说明需要补充元素 —— 将 st1 中的所有元素逐个弹出并压入 st2。这个过程会让 st1 中 “先进栈” 的元素变成 st2 中 “先进栈” 的元素(即顺序被翻转为 “先进先出”)。举例:若 st1 = [3,2,1](1 是最后压入的),执行 while 循环后,st2 = [1,2,3](1 是最先压入的)。此时 st2.pop() 会弹出 1,完美模拟队列的 “先进先出”。5. peek 方法:查看队头元素java运行public int peek() {
return st2.peek();
}
直接返回 st2 的栈顶元素,因为 st2 的栈顶就是队列的队头元素,逻辑与 pop 一致但不执行弹出操作。6. empty 方法:判断队列是否为空java运行public boolean empty() {
return st1.isEmpty() && st2.isEmpty();
}
当且仅当 st1 和 st2 都为空时,队列中没有元素,返回 true;否则返回 false。三、复杂度分析1. 时间复杂度push 操作:仅需一次栈的 push 操作,时间复杂度为 \(O(1)\)。pop 操作:大部分情况下(st2 不为空时),仅需一次栈的 pop 操作,时间复杂度为 \(O(1)\);当 st2 为空时,需要将 st1 的所有元素倒入 st2,此时时间复杂度为 \(O(n)\)(n 是 st1 中元素的数量)。但从均摊复杂度的角度分析,每个元素只会被倒入 st2 一次,所以均摊时间复杂度为 \(O(1)\)。peek 操作:仅需一次栈的 peek 操作,时间复杂度为 \(O(1)\)。empty 操作:仅需判断两个栈是否为空,时间复杂度为 \(O(1)\)。2. 空间复杂度整个数据结构需要两个栈存储元素,空间复杂度为 \(O(n)\)(n 是队列中元素的总数量)。四、拓展与思考1. 为什么用两个栈而不是一个?如果只用一个栈,无法同时满足 “先进先出” 和 “后进先出” 的特性。例如,若元素按 1、2、3 的顺序压入栈,栈中顺序是 [1,2,3](栈底到栈顶),此时弹出顺序是 3、2、1,与队列的 “先进先出” 完全相反。因此必须用两个栈的 “翻转” 操作来实现顺序的转换。2. 代码的边界条件处理在 push 方法中,我们对 st2.isEmpty() 的情况做了特殊处理 —— 直接将元素压入 st2。这是为了避免一种边界情况:当队列中没有元素时,第一次 push 的元素需要直接作为队头,否则 st2 会一直为空,导致 pop 和 peek 操作报错。3. 与官方题解的对比LeetCode 官方题解中,push 操作是无条件将元素压入 st1,而 pop 操作在 st2 为空时才将 st1 元素倒入 st2。这种写法逻辑更统一,但初始队头的处理需要依赖 pop 或 peek 操作的 “倒栈” 逻辑。本文的写法在 push 阶段就对队头元素做了特殊处理,让 st2 始终持有 “当前队头及后续待弹出元素”,在 pop 和 peek 时逻辑更直接,是一种 “空间换时间” 的优化思路(减少了 pop 和 peek 时的判断次数)。4. 其他语言的实现差异Python:没有内置的 Stack 类,可通过 list 模拟(append 为 push,pop() 为栈顶弹出)。C++:可使用 std::stack 容器,逻辑与 Java 完全一致。JavaScript:通过数组的 push 和 pop 方法模拟栈,实现思路完全相同。五、总结用两个栈实现队列的核心是利用 “栈的翻转特性”:输入栈负责接收元素,输出栈负责弹出元素;当输出栈为空时,将输入栈的所有元素倒入输出栈,从而将 “后进先出” 转换为 “先进先出”。本文的实现通过在 push 阶段对队头元素的特殊处理,让 pop 和 peek 操作的逻辑更简洁,同时保证了时间复杂度的均摊最优。这个问题不仅是算法面试的高频考点,更是理解 “数据结构特性转换” 的经典案例,掌握它能帮助你更深刻地理解栈和队列的本质区别与联系。如果你在实际开发中遇到 “需要用栈模拟队列” 的场景(例如某些框架的 API 限制),或者在面试中被问到这个问题,本文的思路和代码一定能帮你从容应对。
