SLAM中的非线性优-3D图优化之轴角在Opencv-PNP中的应用（二）

        本节是上节内容的延续，主要展示如何利用轴角来跟四元数来求解旋转部分的雅可比跟残差，其他不变的地方不重复列出来了，接下来请看精彩内容

一. 罗德里格斯参数化

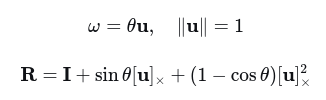
二. 计算各个偏导数

(1)  由于 θ = |w| = √(w_x² + w_y² + w_z²)

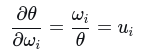
（2）∂uj / ∂wj  

其中δij是克罗内克δ函数

（3） 

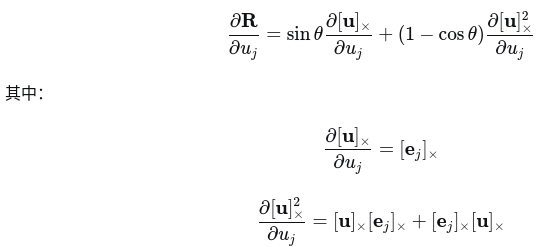
最终通过整合得出结果

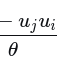
代码中的 dx0dr, dy0dr, dz0dr

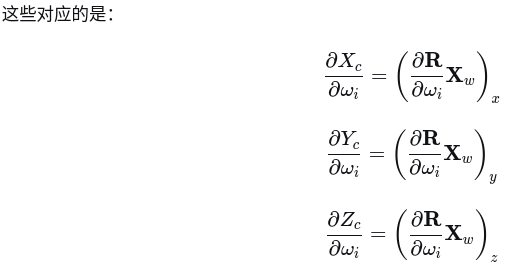
（4） 归一化坐标导数

double dxdr = z * (dx0dr[j] - x * dz0dr[j]);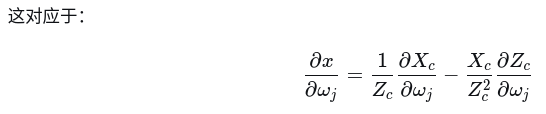

(5) 特殊情况的验证

当theta趋近于0时

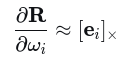
如果只绕单一轴旋转，如z轴

这与直接对旋转矩阵求导的结果一致。

三. 四元数参数化

(1) 旋转用单位四元数表示：

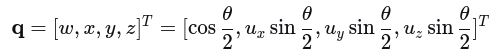
(2)  旋转矩阵与四元数的关系：

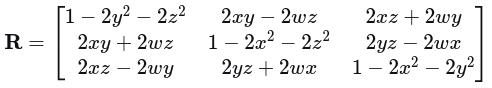
(3) 旋转矩阵对四元数的导数

四元数求导，直接对各个元素求解

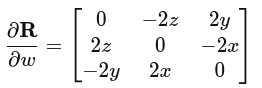
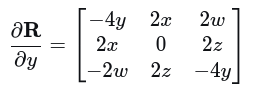
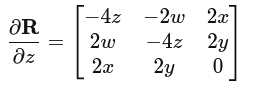
（4）四元数关于相机坐标的导数

一般形式如下：

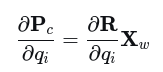
其中qi = {w, x, y, z}

展开对各个分量求导

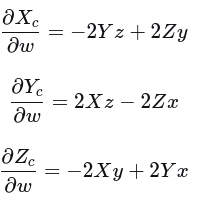
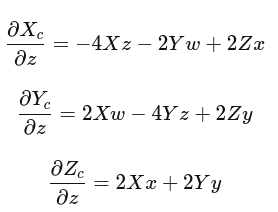
(5) 归一化坐标对四元数的导数

一般公式

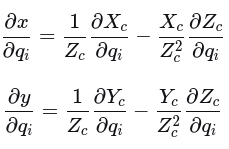
带入即可算出相应雅可比，此处只列出w分量的雅可比，其它的类似

四. 约束处理

      由于四元数是单位四元数，需要处理约束 ||q|| = 1的情况，在优化中常用：局部参数化

使用3维局部扰动：

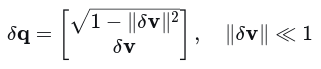
对应的雅可比矩阵

实际优化中使用3×2N的雅可比矩阵：

其中 Jδv→q 表示四元数对局部扰动的雅可比导数矩阵。

（1）问题描述：

在使用四参数无约束优化时可能出现以下问题：

• 迭代过程中四元数可能丢失单位长度特性
• 旋转矩阵的正交性难以保持
• 这些问题会导致数值不稳定性和结果误差

（2）局部参数化方法 

在当前估计值附近定义一个三维局部扰动

其中扰动也是一个单位四元数

最常用的局部参数化：

对于小扰动采用一阶近似：

（3）链式求导：从局部参数到重投影误差，完整的导数链

关键项

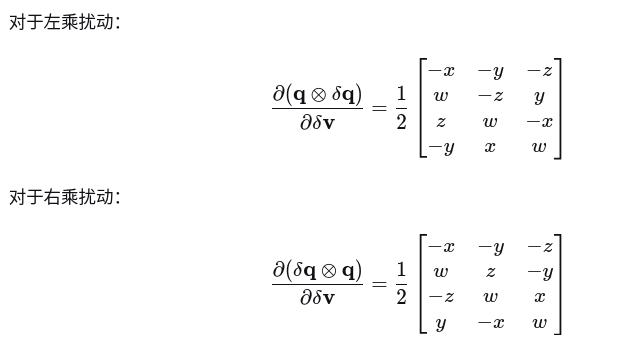
完整的雅可比矩阵计算-旋转部分的雅可比

旋转对重投影误差的雅可比为：

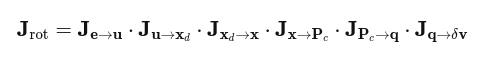
其中Je->u

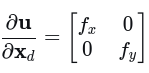
四元数约束处理的关键：

1. 局部参数化：使用3维扰动在切空间中进行无约束优化

2. 链式求导：通过完整的导数链计算重投影误差对局部扰动的雅可比

3. 指数映射：将局部扰动映射回单位四元数

4. 数值稳定：通过归一化保证四元数始终在单位球面上

总结

四元数的核心优势：

1. 无奇异性：完全规避万向节锁问题
2. 数值稳定性：单位四元数确保旋转矩阵正交性
3. 插值特性：支持自然的球面线性插值

与罗德里格斯参数的比较：

1. 参数维度：

   • 四元数：4参数（带约束条件）
   • 罗德里格斯：3参数（无约束优化）

2. 计算特性：

   • 四元数：导数计算更复杂但数值稳定
   • 罗德里格斯：计算更简单但存在奇异点

3. 应用场景：

   • PnP问题：倾向于使用罗德里格斯参数
   • SLAM系统：更常采用四元数表示

四元数求导要点：

• 保持链式法则的一致性
• 需计算旋转矩阵对四元数各分量的偏导
• 需处理单位范数约束条件
• 数值优势体现在大角度旋转场景

实际应用建议： 在PnP等优化问题中，罗德里格斯参数因其简洁的无约束形式更具实用价值，而四元数更适合需要数值稳定性的SLAM系统。