当前位置：首页 > news >正文

m序列原理及在5G的应用

news 2025/11/14 6:27:15

一、m序列概述

数学上，序列是被排成一列的对象（或事件）；每个元素不是在其他元素之前，就是在其他元素之后。如果排列的对象是二进制比特0或1，称为二进制序列。二进制序列是坐标轴上的0和1两个点组成的序列，不同点可以重叠。

如果排列的对象是整数，那么称为整数序列。整数序列是横或纵坐标轴上的一个个的点组成的序列，点可以重叠。

如果排列的对象是复数，那么称为复数序列。复数序列是平面坐标中的一个个的点组成的序列，点可以重叠。可以预先确定并且可以重复实现的序列称为确定序列；既不能预先确定又不能重复实现的序列称随机序列；不能预先确定但可以重复产生的序列称伪随机序列。

二、m序列的原理

m序列，全称为最长线性反馈移位寄存器序列，是伪随机序列的一种，也是最基本的扩频码之一。

1. 核心生成结构：线性反馈移位寄存器

m序列由一个n级线性反馈移位寄存器产生。

移位寄存器：由一系列触发器（D Flip-Flop）组成，每个触发器存储一个比特（0或1）。在时钟脉冲驱动下，每个触发器的值会移交给下一个。

线性反馈：将寄存器中某些特定级（称为抽头）的输出进行模二加（即异或运算，XOR）后，再反馈到第一级的输入。

这个结构可以用一个本原多项式来精确描述。例如，一个3级的LFSR，其本原多项式可以是： f(x)= 。这表示：

x3 代表第3级。
x 代表第1级。
1 代表第0级（即直接输入）。
抽头位于第3级和第1级，将它们进行异或后反馈到输入。

2. m序列的关键特性

正是这些卓越的特性，使其在通信系统中备受青睐。

平衡性

在一个周期内，“1”的个数比“0”的个数多一个。

例如，一个长度为7的m序列：1 1 1 0 0 1 0，其中有4个‘1’和3个‘0’。

游程分布特性

“游程”是指连续的相同码元（全‘1’或全‘0’）段。

在m序列中，长度为1的游程约占1/2，长度为2的游程约占1/4，长度为3的游程约占1/8，以此类推。这个分布非常接近随机序列。

移位相加特性

一个m序列与其循环移位后的序列进行模二加，得到的是另一个循环移位的同一m序列。

这个特性对于同步捕获至关重要，因为接收机可以通过本地序列与接收序列的滑动相关来寻找峰值。

良好的自相关特性

这是最核心、最重要的特性。

自相关函数描述了一个序列与其自身移位后的相似程度。

对于理想的m序列，其周期自相关函数是二值的：

零移位时：相关值达到峰值（等于序列长度N）。
非零移位时：相关值恒为 -1（如果使用±1表示，0映射为+1，1映射为-1）。
公式：
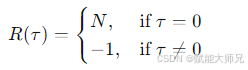
深入理解：这个尖锐的“冲激函数”状的自相关峰，使得接收机能够极其精确地判断序列是否对齐。在同步过程中，接收机不断调整本地m序列的相位，并计算与接收信号的相关值。一旦相关器输出一个巨大的峰值，就意味着同步完成。这个尖锐的峰值能有效抵抗多径和噪声的干扰。

预知性和可重复性

虽然看似随机，但m序列是完全由初始状态和反馈逻辑决定的，因此是确定性的、可再生的。发送端和接收端只要使用相同的生成多项式，就能产生完全相同的序列。

三、m序列在NR PSS中的应用

在5G NR中，主同步信号是下行同步的第一步，其设计直接关系到手机能否快速、可靠地接入网络。

1. NR PSS的设计选择

与LTE使用Zadoff-Chu序列不同，NR PSS选择了m序列（更具体地，是采用BPSK调制的m序列）。

序列长度： 127位。这比LTE的PSS（62位）要长，提供了更强的处理增益和抗干扰能力。

序列生成：由一个7级LFSR生成，其本原多项式为：。

对应的抽头为第7级和第4级。
初始状态（即LFSR的种子）被固定为 [1,1,1,0,1,1,0]。

2. 为什么NR PSS选择m序列

这是一个关键的设计权衡，主要基于以下原因：

对频偏的强鲁棒性

核心原因：Zadoff-Chu序列对频率偏移非常敏感，频偏会破坏其理想的互相关特性，并导致相关峰分裂和偏移。

m序列的自相关特性受频偏影响较小。在初始同步阶段，手机尚未进行精细的频率校正，可能存在较大的频率误差。m序列能确保在存在频偏的情况下，相关峰仍然保持尖锐和稳定，不会分裂或严重偏移，大大提高了初始同步的可靠性。

深入理解：这对于高频段（如毫米波）通信尤为重要，因为同样的振荡器精度在更高载波频率上会产生更大的绝对频偏。

更简单的相关器实现

m序列的相关器可以通过简单的移位寄存器和加法器实现，硬件复杂度相对较低。
虽然ZC序列可以利用FFT实现高效相关，但在最简单的接收机设计中，m序列的时域滑动相关实现起来更直接。

丰富的序列数量

一个n级LFSR能产生的不同m序列数量由本原多项式的数量决定。

对于PSS，NR定义了3个不同的序列，对应3个不同的物理层小区ID（0, 1, 2）。这3个序列是通过对同一个基础m序列进行循环移位得到的。

循环移位量分别为 0, 43, 86。之所以选择这些较大的移位量，是为了确保三个序列之间的互相关性足够低，防止手机将一个小区的PSS误判为另一个小区。

3. NR PSS的生成和映射过程

生成基础m序列：

使用固定的LFSR（多项式，初始种子 [1,1,1,0,1,1,0]）生成一个长度为127的m序列，记为d(n)。

生成三个PSS序列：

对于小区ID 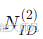=0,1,2，分别对基础序列 d(n) 进行循环移位，得到PSS序列 s(m)：
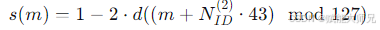
这里的 1−2⋅(⋅) 操作是将0/1比特映射为BPSK符号+1/-1。

映射到资源网格：

PSS被放置在同步信号/PBCH块（SSB）的第一个OFDM符号上。

它占据频域中心的127个子载波（在SSB的240个子载波中间），两边的子载波留作保护带。

四、总结

从LTE到NR的演变哲学： LTE选择ZC序列是看重其理想的循环自相关和互相关特性，以及OFDM系统中等效的低PAPR。然而，实践表明，在初始同步的恶劣环境下（大频偏、低信噪比），m序列的稳健性比ZC序列的理论完美性更为重要。NR的设计回归务实，选择了在现实条件下更可靠的m序列。

m序列在NR PSS中的角色：它充当了一个在时域和频域都存在巨大不确定性的环境中，一个清晰、尖锐、稳定的“灯塔”。手机通过在整个频带和时间上进行滑动相关搜索这个“灯塔”的尖锐峰值，一旦找到，就同时确定了：

符号定时：知道SSB的起始位置。
频率粗同步：因为m序列对频偏不敏感，相关峰位置准确。
小区组内ID：通过判断是三个序列中的哪一个，获取。
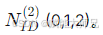权衡的代价：使用m序列的主要代价是其互相关性不如ZC序列理想。但在PSS这个特定场景下（只需要区分3个序列），通过精心选择足够大的循环移位（43和86），可以有效地规避这个问题。