算法（二）滑动窗口

一、长度最小的子数组

209. 长度最小的子数组 - 力扣（LeetCode）

1.暴力解法

暴力解法其实也好说，大概分成三步吧：

第一步用一个变量当成指针，看看单个的值能不能符合>=target，符合就返回len = 1，不符合就进入下一步。

第二步就是，因为后面遍历都不再是一个一个值，因为第一步遍历完了，如果用区间的形式遍历，双指针就是不二之选。

当然，第一步和第二步其实可以合并。

不合并的话大概就是：

for(size_t i = 0;i < nums.size();i++)

{

        //判断

}

int left = 0;

int right = left + 1;

while(left < nums.size() - 1)

{

        while(right < nums.size())

        {

                //判断

        }

}

合并的话就是：

int left = 0;

int right = left;

while(left < nums.size() - 1)

{

        while(right < nums.size())

        {

                //判断

        }

}

大差不差。

第三步

其实可以直接返回，判断的逻辑就是判断这个区间内所有值和是否大于等于target，不断更新len变量；

如果不在判断逻辑里实现，那可以记录下来所有的区间，记录完以后判断最短的是谁，等于是第一次说的直接返回那种的时间换空间。

2.滑动窗口

在暴力解法中我们发现了一些规律：

规律1

没有必要枚举所有的情况，原因如下：

数组里的元素全部都是正整数，一旦找到符合>=target的区间，那么之后再也不用往后记录了，因为符合条件以后再加正整数一定是符合>=target的条件，但是

在此次定left，移动right的结果下，再往后遍历的子数组的长度肯定要大于第一次找到的子数组的长度。

规律2

到时候肯定是外面一层循环定left，里面一层循环动right，完全可以用一个变量sum每次++right后+=right指向的值，再进行判断，如果符合条件，且比len小就更新len，不符合或者不比记录下来的len小就不用更新。

这样省去暴力算法中由于只记录区间不计算大小的时间消耗。

算法内涵

可以发现，外层的left是一直往右走的，内层的right每次也是从left位置往右走的，俩人还不是我们学习的传统双指针那样相向而行而是同向而行。

不知道背单词的时候大家有没有用过某些单词书里面送的那种卡，可以盖着释义，如果想看的话就往右移一移，就类似于：

单个的看，是不是就好像固定一端，另一端类似于窗口、窗帘一样往右拉。

所以同向双指针，就被称为滑动窗口。

代码表达

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int len = 0;for (size_t i = 0; i < nums.size(); i++){int left = i;int right = left;int sum = 0;while (right < nums.size()){if (sum < target)sum += nums[right++];else{if (sum >= target)if (len == 0){len = right - left;break;}else{len = len <= right - left ? len : right - left;break;}}}}return len;}
};

第一版代码是这样的，走读代码发现：

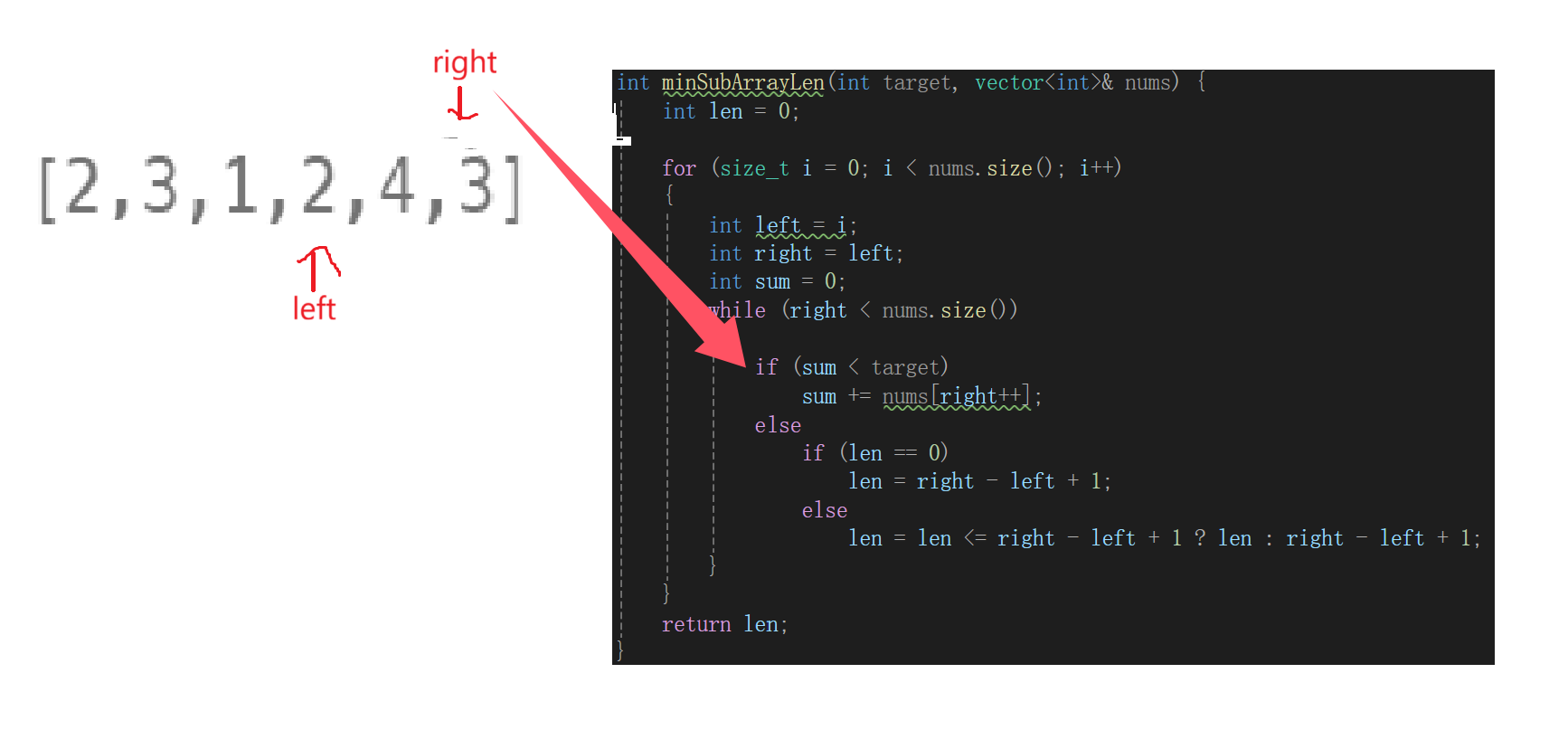
这种情况按理来说应该被判断是否符合len，但是由于我们写的循环每次要不然只支持变更sum，要不然只支持判断，难免会有：

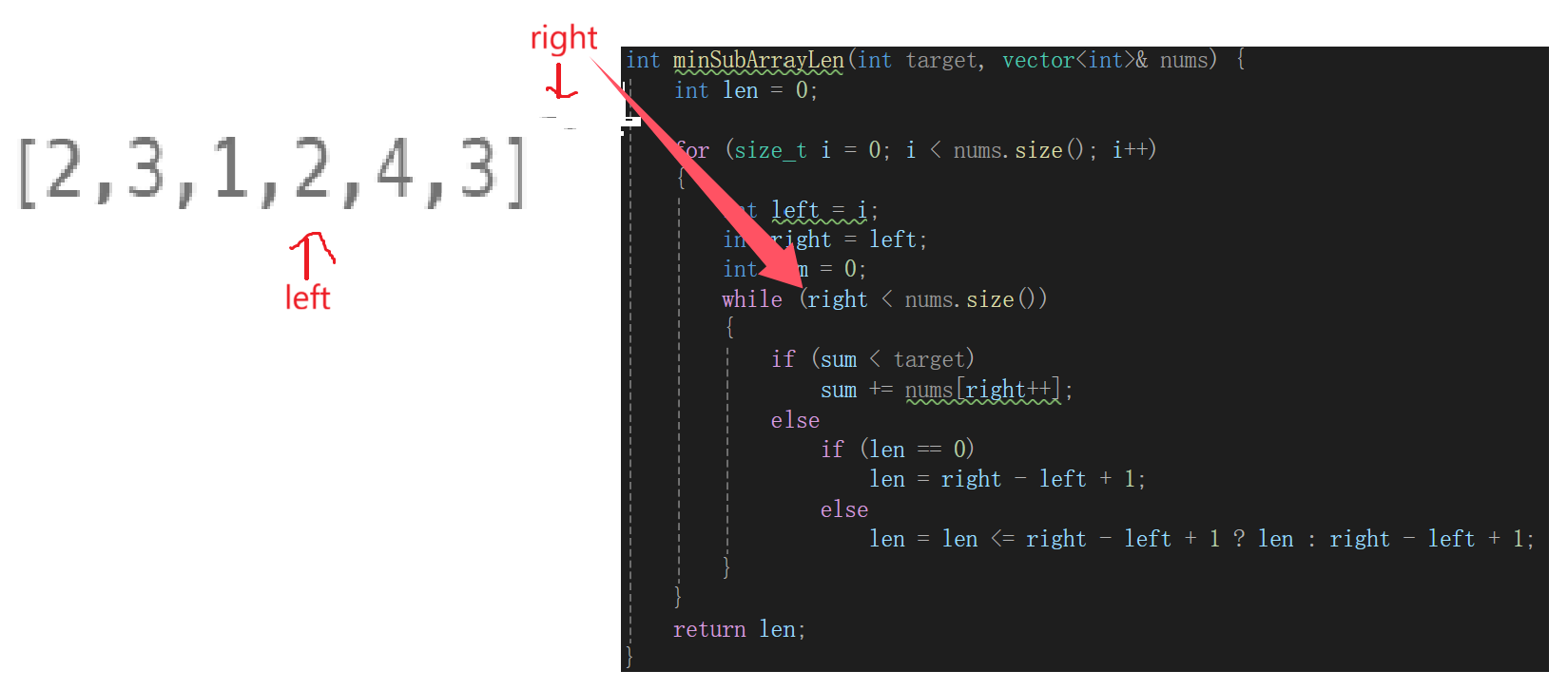
没有被记录，万一是最后要求的正确情况就完了，内层循环完检查一下：

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int len = 0;for (size_t i = 0; i < nums.size(); i++){int left = i;int right = left;int sum = 0;while (right < nums.size()){if (sum < target)sum += nums[right++];else{if (len == 0){len = right - left;break;}else{len = len <= right - left ? len : right - left;break;}}}if (right == nums.size() && sum >= target)if (len == 0)len = right - left;elselen = len <= right - left ? len : right - left;}return len;}
};

这段代码就这么拿过去，就发现问题了，这里面的数就几百几千，如果要加到几个亿，每次代价是很大的，也就是每次循环right = left重新算，太麻烦了，所以我做了这样的操作：

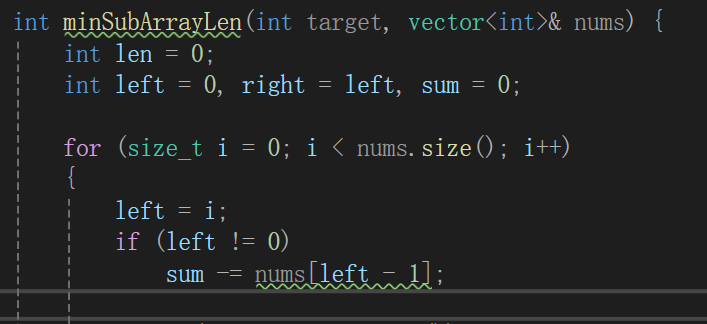
其它地方不变，加了这样的操作，意义是：

比如这次不是找到目标值了嘛，最后遍历完实际上指针是这样的：

红色部分是计算sum的区间。

下次循环我不让right再回去了，直接检测left到right-1位置的值，这样省去了(right - left) * n次循环（内层循环）。

为什么这么做没问题呢？

下次++left后第一次计算的区间应该是这样的：

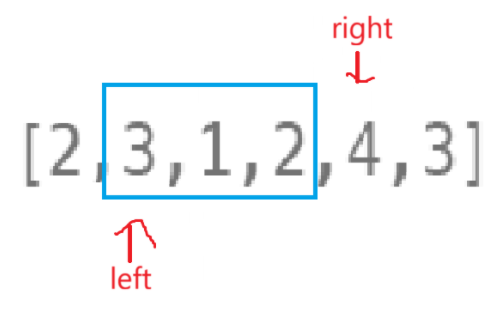
• 如果此时区间内所有的值的和sum不够target，那么下面的循环还会让right右移继续遍历，这一点循环完成：
  
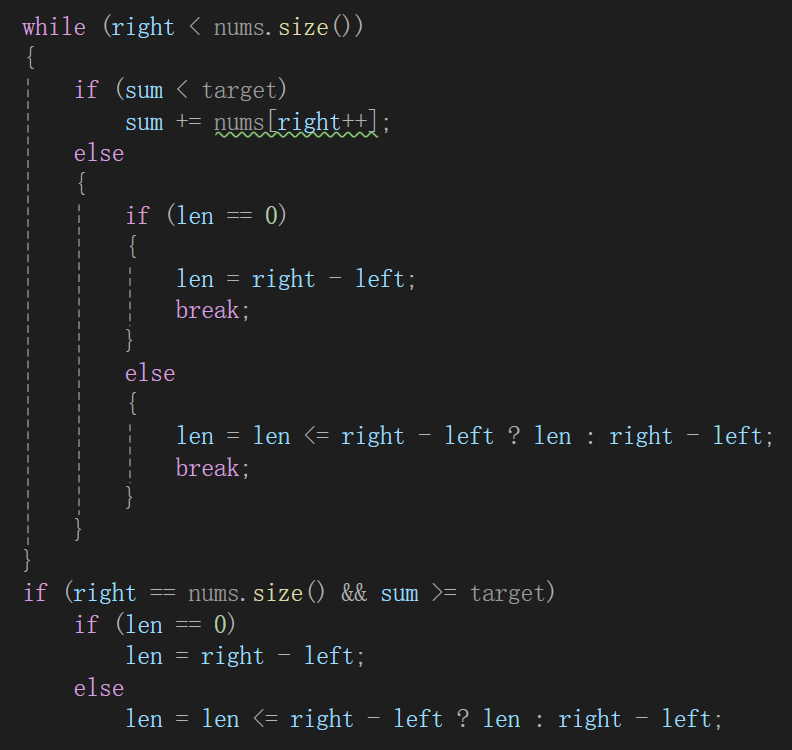
• 如果此时区间值符合sum>=target，那么需要不需要right左移呢？

你想一个事，这次遍历的上一次遍历，是不是取的最短实现条件的区间，没毛病吧，说明刚好：

是符合条件的。

也就是这里加上最后一个2才符合条件，有可能是这最后一个数非常大，所以加上了才能符合条件。假设就说现在left没变：

--right的sum肯定就小于target，更别说如果既--right又++left。

所以一次检测后，下一次检测的right只能从上次检测的right后移或者不动，不可能前移。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int len = 0;int left = 0, right = left, sum = 0;for (size_t i = 0; i < nums.size(); i++){left = i;if (left != 0)sum -= nums[left - 1];while (right < nums.size()){if (sum < target)sum += nums[right++];else{if (len == 0){len = right - left;break;}else{len = len <= right - left ? len : right - left;break;}}}if (right == nums.size() && sum >= target)if (len == 0)len = right - left;elselen = len <= right - left ? len : right - left;}return len;}
};

二、无重复字符的最长子串

3. 无重复字符的最长子串 - 力扣（LeetCode）

结合典例很容易看出来要求的是什么。

1.暴力解法

暴力解法很容易想到，还是双指针：

我的思路是这么出来的，肯定得有一根指针，从前往后一直遍历字符，每次遍历总得知道跟前面遍历过的字符串重复了没吧，所以总得有一根指针记录未重复的字符串从哪开始，所以双指针呼之欲出了。

正常循环就是left站岗，right遍历：

暴力解法的时间复杂度主要取决于每次right更新以后，都得从left位置遍历到right - 1位置，看看是否重复。检测是否重复又得来一根指针。

不重复right继续走；

重复记录一下长度，left跳过已记录过的不重复字符串的头，即++left;

大概解决办法就是：

两根指针，最终结束的条件是：

最后一次遍历应当是这样的场景，由right - left记录一下最后一个不重复字符串，记录完left = right，所以结束应该是left遍历到最后。

大致代码：

int left = 0,right = 1,pcur = 0,len = 0;

while(left < size)

{

        whille(right < size)

        {

                //重

                while(pcur >= left && pcur < right)

                {

                        if(s[pcur] == s[right])

                        {

                                len = right - left;

                                ++left;

                                pcur = left;

                                right = left + 1;

                                break;

                         }

                        else

                                ++pcur;

                }

                //不重

                ++right;

        }

}                

有细节没有处理，主要是大概写写，考虑考虑时间复杂度，很明显，left从头到尾没有走回头路right还有走回头路的嫌疑，俩人最坏能走O()，只不过内层pcur不断的走回头路，最坏情况下，如果字符串完全不重，pcur自己都能走个O()，再一乘，最坏情况直接O()。

2.滑动窗口

可以发现left和right指针始终是维护着一个区间，但是right有走回头路的情况，如果想要使用滑动窗口的思想，那么两个指针绝对是不能走回头路的，都朝一个方向移动，时间复杂度最大也就是O(n + n)。

不过尝试之前，解决判断是否重复问题非常重要，因为就算滑动窗口出来了，O()的去重也是个麻烦事。

这次我不再用指针遍历的方式，转而运用哈希表，因为不重复的字符肯定在哈希表里的值<=1，重复的字符肯定在哈希表里的值>1，这样时间复杂度直接降到O(1)，有了这个保障以后，放开手脚看看能不能实现滑动窗口。

假设我们已经设计好了记录代码，按照我们暴力解法，应当是：

因为在上述字符串中，以a开头的最长的字符串已经被记录了，应该右移left，继续循环，但是实际上++left是非常低效的。

原因是以a开头的非重复字符串是：

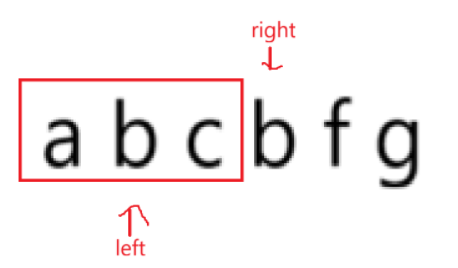
如果left不跳过重复字符，所遍历到的长度一定比刚才小。

可能这个还是不太直观，如果：

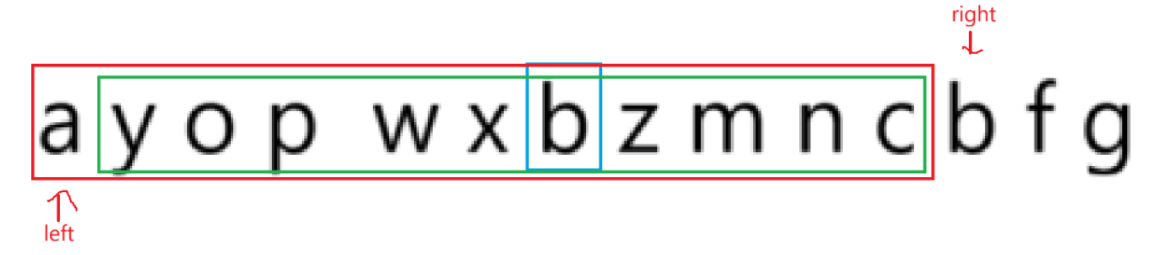
这样总够直观了吧，也就是一旦碰见重复字符，完全可以让left一直移动到重复字符的右侧，否则遍历得到的字符串永远比第一次找到的小。所以在此区间内从以第一个字符到重复字符为头的字符串均可以不用再遍历了。

在这样的前提下：

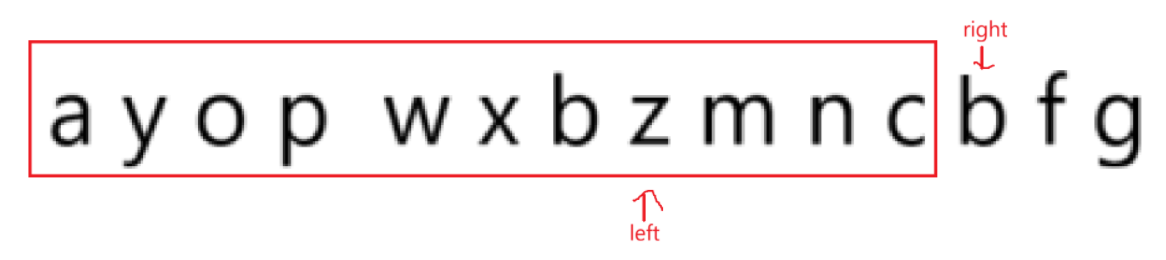
可以很明显的观察到，重复字符到重复字符之间的z m n c绝对不会重复，唯一的重复字符b已经被剔除了，right根本不用回来判断，因为此时的left到right绝对没有重复字符。

这样的话暴力解法找重复的问题化解为O(1)，right走回头路的问题解决了，并且使得left实现了一定程度的优化。

这样的话最后循环结束条件也很简单，right的值。

两个指针同时向一个方向移动就要用滑动窗口，滑动窗口的一般逻辑是：

进窗口是移动right，出窗口是移动left。

对于这道题也就是：

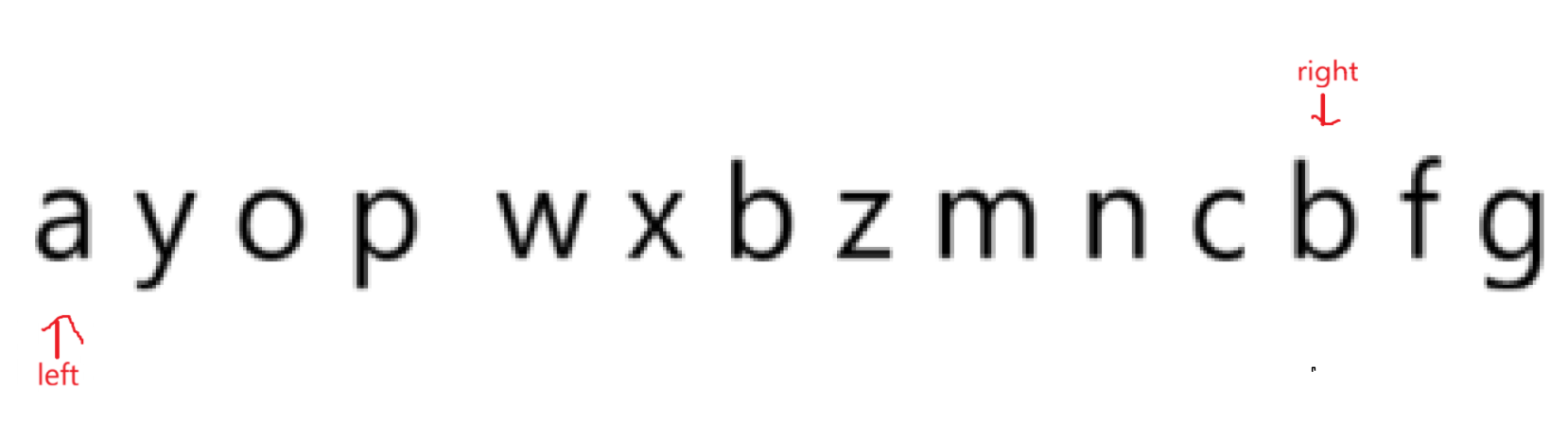
进窗口right遍历每个字符，而且做到每个字符入哈希表;

判断条件就是哈希表里存的值>1；

碰到元素>1，很明显就得出窗口移动left，并且left需移动到重复字符的右侧。

最后提一嘴哈希表：

哈希表只要容纳到可以放得下这几个字符就行，这几个字符ASCII码值最大也就超不过128，因此：

class Solution {
public:int lengthOfLongestSubstring(string s) {int left = 0,right = 0,len = 0;int hash[128] = {0};while(right < s.size()){hash[s[right]]++;while(hash[s[right]] > 1){   len = len > right - left ? len : right - left;hash[s[left++]]--;}++right;}//越界len未记录len = len > right - left ? len : right - left;return len;}
};

滑动窗口写起来其实也没多少，主要是画图给我画吐了快，做这一道题带着写文章画了十几个图，俩指针快夹死我了。

三、最大连续1的个数

1004. 最大连续1的个数 III - 力扣（LeetCode）

思路：

这题把维护区间又甩脸上了，所以肯定得分析left和right的运动规律。

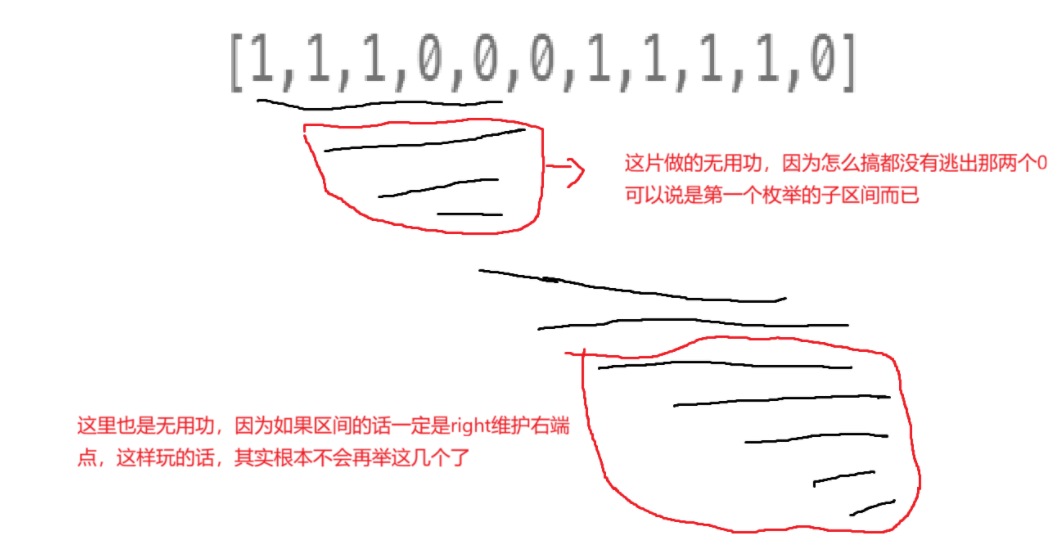
left指针站着不动，right一直往右找0，直至维护的区间的0的个数==k。

依旧是拿着样例暴力枚举，然后就发现一个事，枚举只++left如果不变更区间内0，那么举出来的区间将会一直是上一次出窗口更新结果的子区间。这是无用功。

这也就要求我们根据区间内的0变更left的位置。

那么left更新的标准是什么呢？

光看那一个例子我也是在看不出来，因此呢，又拿一个样例，我这次感受到了，只要让left一直++，如果碰到第一个0，那就可以跳过它，因为此时right是不变的，那么区间内维护的0的个数会--，这样就相当于新区间了，绝对的新，不是子区间。

在这个过程中left和right都只右移，其实还是滑动窗口。

有了思路以后先别急写代码，维护区间的标准是啥，也就是用到啥变量来维护滑动窗口：

left

right

count//计数，记录窗口内0个数，可以作为出窗口的标准，也可以作为更新left的标准

len//最后返回长度，所以还得搞一个len

当然，其实临界没分析：

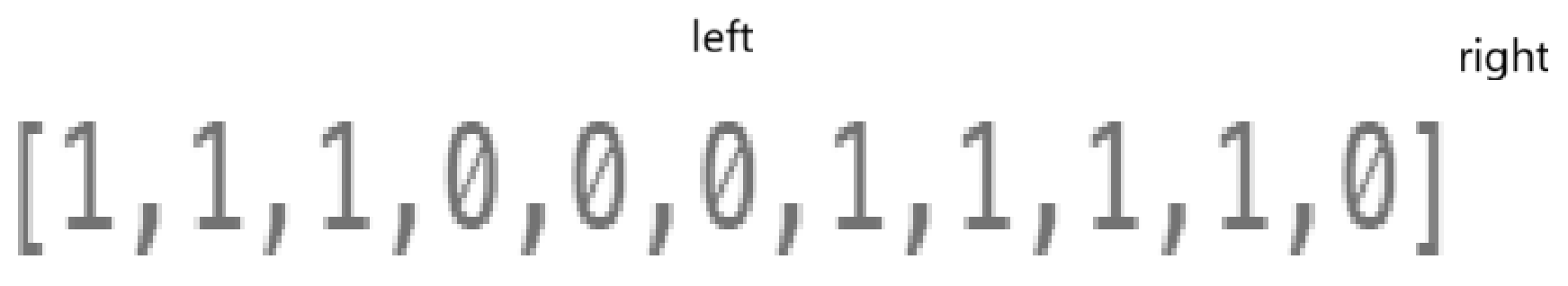
最后大概率就是这样的指针排布，所以呢，循环条件也出来了，并且出了循环还得再计算一下最后一个区间。

小细节问题：

class Solution {
public:int longestOnes(vector<int>& nums, int k) {int left = 0;int right = 0;int count = 0;int len = 0;while(right < nums.size()){if(count <= k){if(nums[right] == 0)++count;++right;}                else{if(len == 0)len = right - left;elselen = len >= right - left ? len : right - left;while(left <= right){if(nums[left] == 0)break;++left;}++left;--count;}} len = len >= right - left ? len : right - left;return len;}
};

代码哪里出问题了呢？

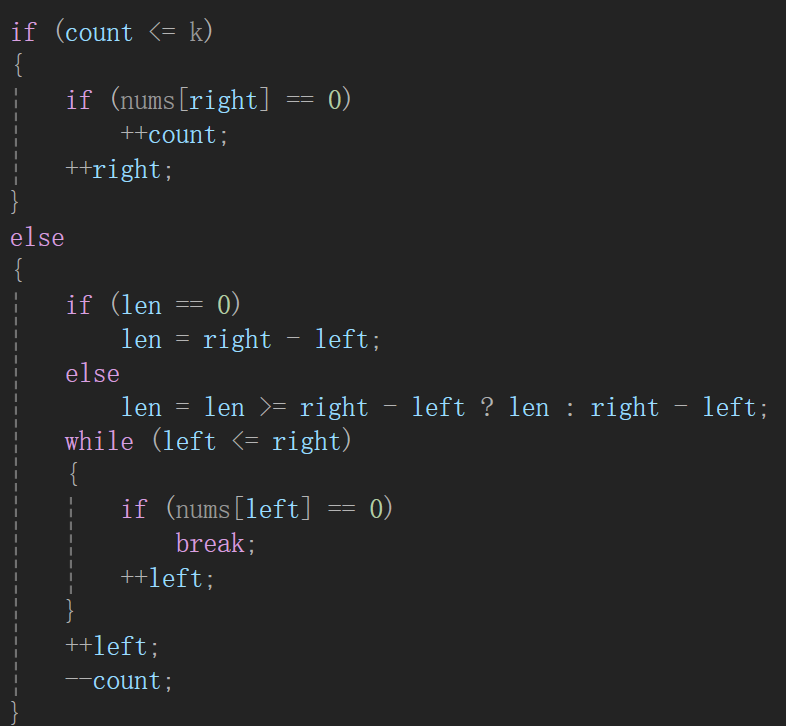
if倒是没啥问题，因为即使count == k，碰不到0就还得一直++right。

但这么写的话，到时候计算len，不太对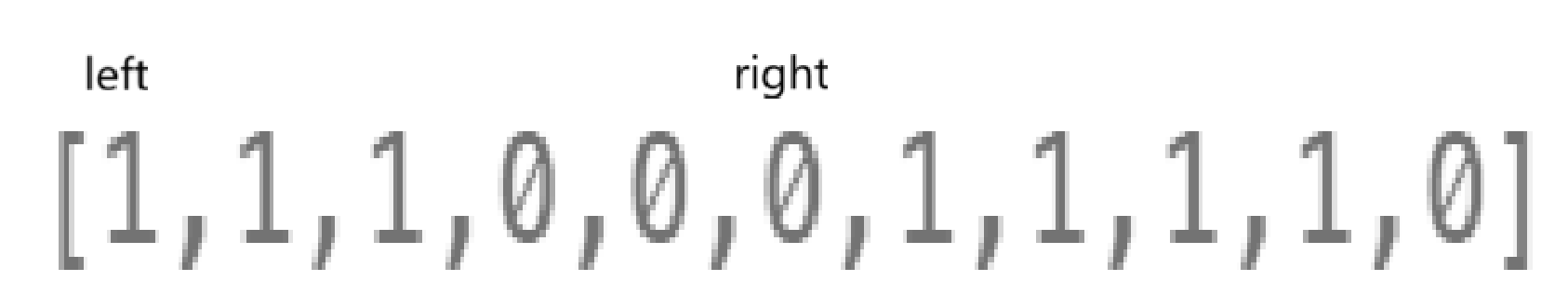

按照上面的逻辑，那么只有right遍历三个0才能找到正确答案。

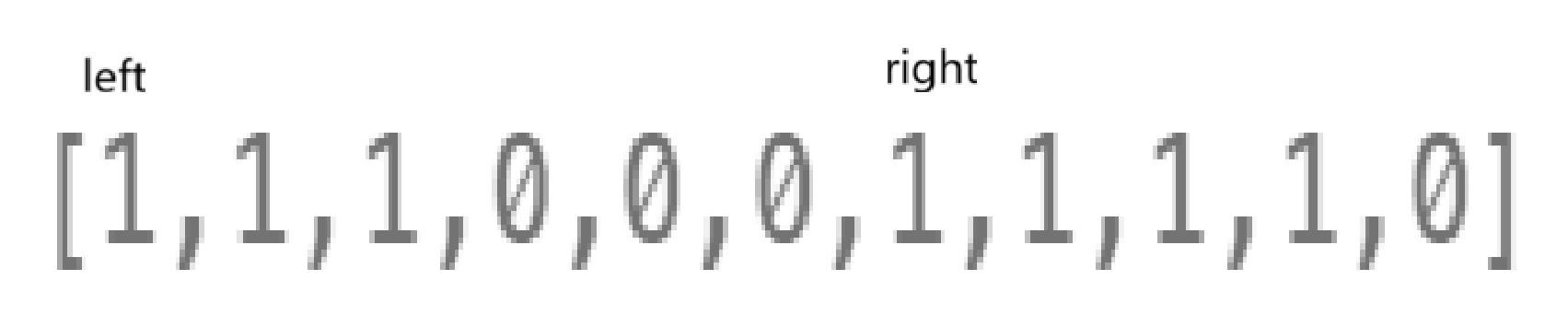
这么搞不太对，right错位了，所以我修改了一下：

class Solution {
public:int longestOnes(vector<int>& nums, int k) {int left = 0;int right = 0;int count = 0;int len = 0;while (right < nums.size()){if (count < k){if (nums[right] == 0)++count;++right;}else{if (count == k && nums[right] == 1)++right;else{if (len == 0)len = right - left;elselen = len >= right - left ? len : right - left;while (left <= right){if (nums[left] == 0)break;++left;}++left;--count;}}}len = len >= right - left ? len : right - left;return len;}
};

如果count < k，那其实肆无忌惮往后遍历就可以，只不过碰见0记得++count；

如果count == k，是1的话你还遍历；

不是1的话说明又right碰见0了，这个时候更新left，也就是出窗口更新。

直接跑过：

怎么说呢，反正做这道题就是暴力->优化暴力->试运行->改bug。

我现在的水平写算法题还是处于if和else关联没那么强，或者说，知行合一没那么强，因为规律分析的好好的，结果写代码right走多了。

四、将x减到0的最小操作数

1658. 将 x 减到 0 的最小操作数 - 力扣（LeetCode）

这个题当滑动窗口还是太阴了，因为看个草图：

每次只能从数组最左边和最右边进行选取，最终目的是选最少的数的个数，使得它们的和等于x。

假如你想要它说啥做啥，也就是直接暴力，你看看行不行昂：

上来有俩选择：

l或者r

下一步也是俩选择：

l或者r

以此类推，到最终会有两种结果==x或者>x，如果==就不说了；>x你可就等着遭罪吧，因为相当于你上次举例不合适了，等于你这个路径得被废弃，我根本想不到循环逻辑啊！

因为看起来选左选右没什么优先级啊，随机的分支写啥循环？

为什么说费劲呢？

正难则反

从两边选真的太难了，所以反过来去中间选，选什么呢？

假如：

现在不从两边找和等于x，而是从中间找一个连续的区间，使得和为sum - x，sum即为数组所有元素的和。

咱也不看具体例子，直接上最狠的抽象图：

中间维护的是连续的区间，因此还是整双指针解决。

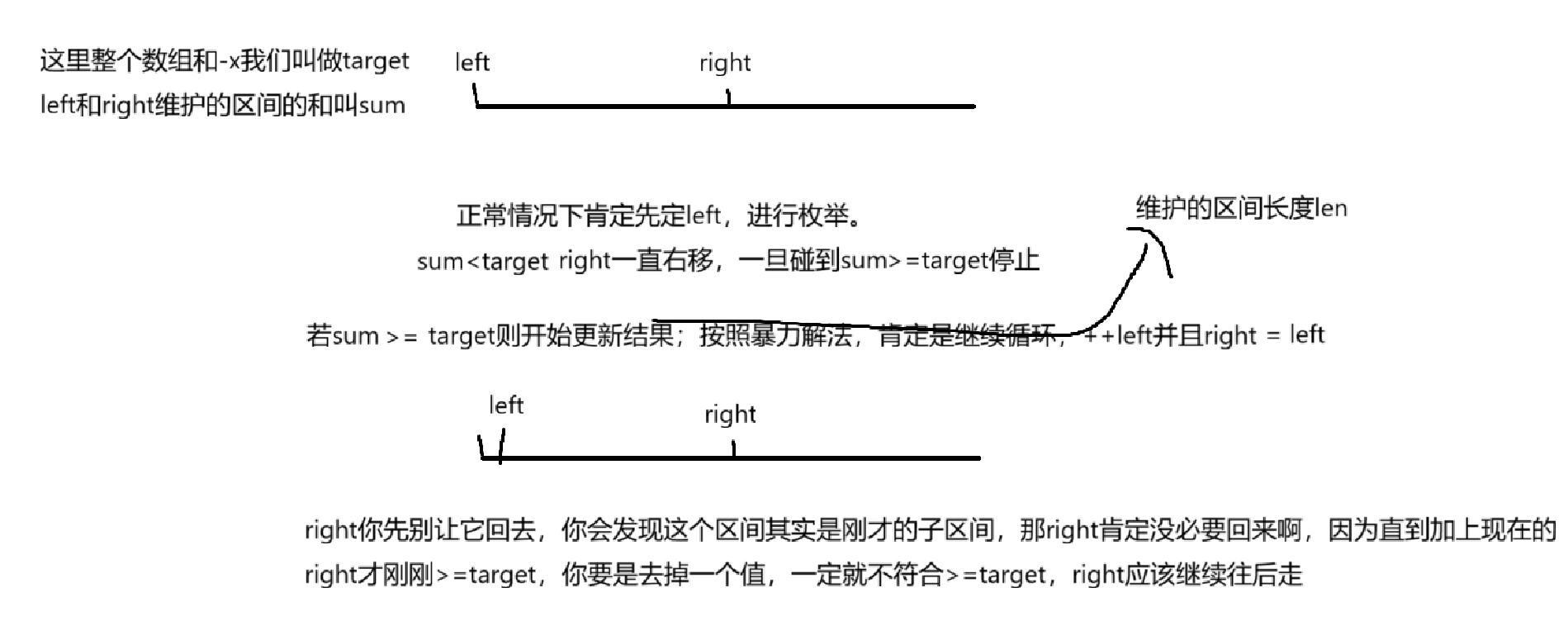
大致就这个逻辑，循环肯定极端还是看right越界了没有，可能还有边界处理，这一点我马上给出具体例子说明，现在大体出来了，就是循环+三分支。

注意到left和right都只向右移，那么就是滑动窗口的思路。

边界处理：因为本来维护的区间是[2,3]，不够6，肯定还会继续++，主要还是取决于==的条件怎么写，是此时left和right占的位置刚好还是right多走一步。

另外，由于要两端最短，所以等于要求len最长。

class Solution {
public:int minOperations(vector<int>& nums, int x) {int left = 0;int right = 0;int sum = 0;int target = -x;int len = 0;//计算targetfor(auto& e:nums){target += e;}//开始维护区间while(right < nums.size()){if(sum < target){sum += nums[right];++right;}else if(sum > target){++left;sum -= nums[left - 1];}else{len = len >= right - left ? len : right - left;++left;sum -= nums[left - 1];}}if(sum == target)len = len >= right - left ? len : right - left;return nums.size() - len;}
};

初始代码我就写成这个样子了，因为我是按照一定会有组合使得和为x，因为sum < target的行为是，先把这次的加了，直接后移right，所以right会多走一步形成[left,right)区间，这一点影响len的计算，也影响最后越界还得判断处理。

但是写完我发现个问题嗷：

要是不存在呢？

比如上面这个例子，所以还得拿我们代码走走看看，到底不存在是怎么个事。

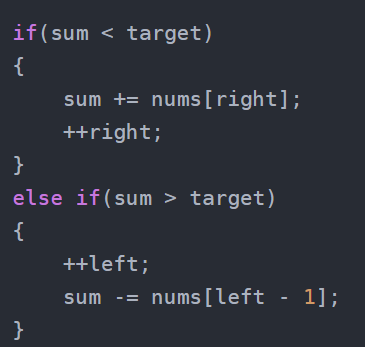
不难发现上面这个例子只走这俩。

而且：

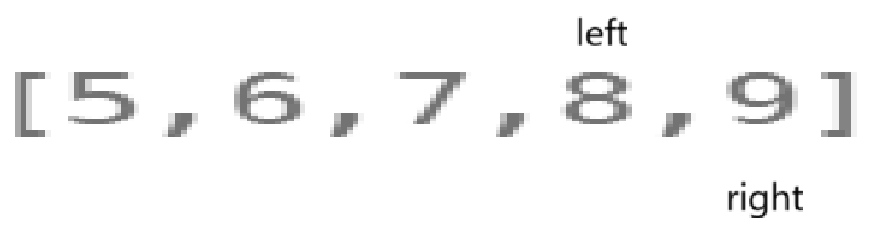
指针一直都是这个样式的，一追一赶的。

right刚把5加上，就发现不对劲了，那么又该++left，-= nums[left - 1]。

之后一直都是刚加上的数下一次循环就给它减掉，所以呢其实这个问题也好说：

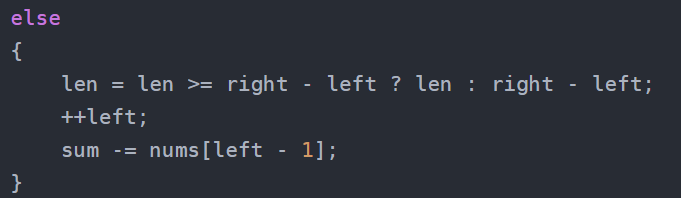
不是只有相等才会该len嘛，这样的话，给len初始值干成-1不完了。

同时：

这个情况是每个都比x大，一减成负数了；

由此我就想到，如果全部加起来都没x大，那岂不是也没值，这也得返回-1,我是这么写的：

但是还是炸了：

按道理left一步一脚印，right没必要回来，咋就出问题了？

大概走读以后发现是边界处理的问题。因为我们维护的left最终改在4，right改在nums.size()。

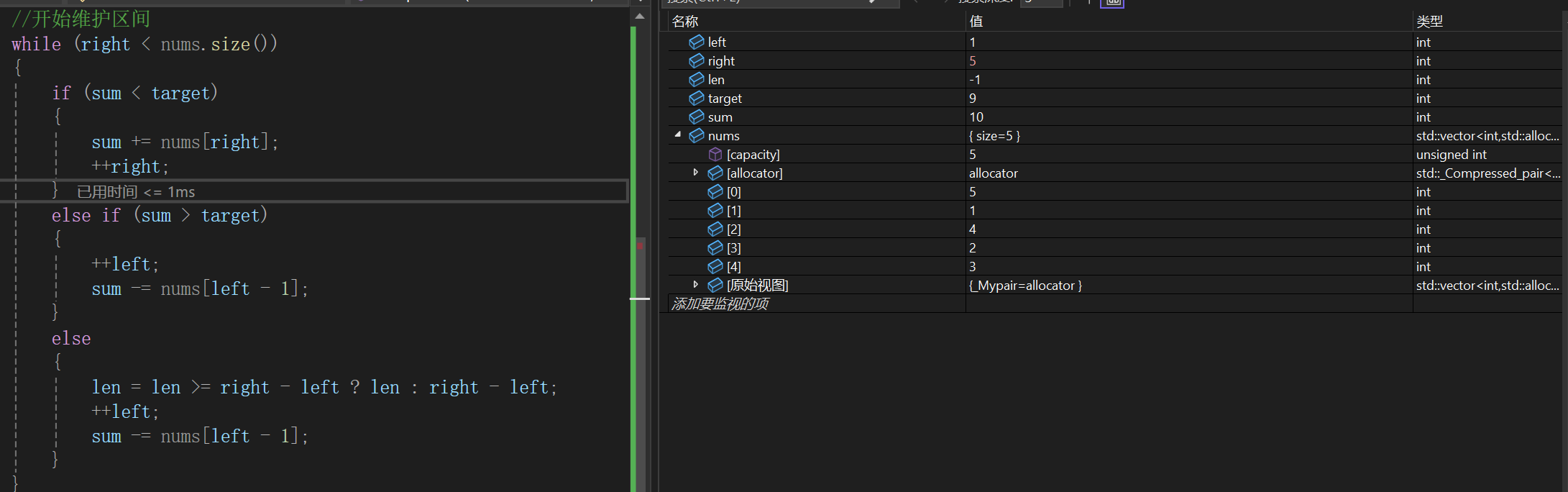
倒到VS下一调试，发现其实是少走了一步边界判断，边界判断不够全，我当时考虑的是如果sum小的话，没必要管；如果sum ==的话肯定得更新；没管sum >咋办，我个人倾向直接整个while罩着>target的情况，说不定需要减好几次嘞，主要这样最省事，不用动脑筋思考，因为你思考出来就一次还行，思考出来两次多次不还得循环。

class Solution {
public:int minOperations(vector<int>& nums, int x) {int left = 0;int right = 0;int sum = 0;int target = -x;int len = -1;//计算targetfor(auto& e:nums){target += e;}if(target < 0)return -1;//开始维护区间while(right < nums.size()){if(sum < target){sum += nums[right];++right;}else if(sum > target){++left;sum -= nums[left - 1];}else{len = len >= right - left ? len : right - left;++left;sum -= nums[left - 1];}}while(sum > target){++left;sum -= nums[left - 1];}if(sum == target)len = len >= right - left ? len : right - left;return len == -1 ? -1 : nums.size() - len;}
};

除了循环先执行这个：

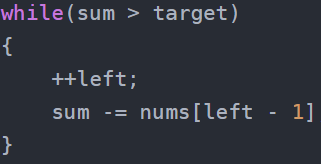
这样大于可能变等于变小于，小于不用管，等于还有承接。

不耽误，虽有波折，但总归还是过了。

五、水果成篮

不管难不难吧，反正看这题长度就烦的不行。

确实要求挺抽象：

拿这个例子理解就是，你可以随便选一个树开始摘水果，摘了以后往后走；

就俩篮子，等于最多摘俩种类的水果。

就它这个维护区间且left和right都只能往右走，基本又滑动窗口。

思路直接就一激灵：

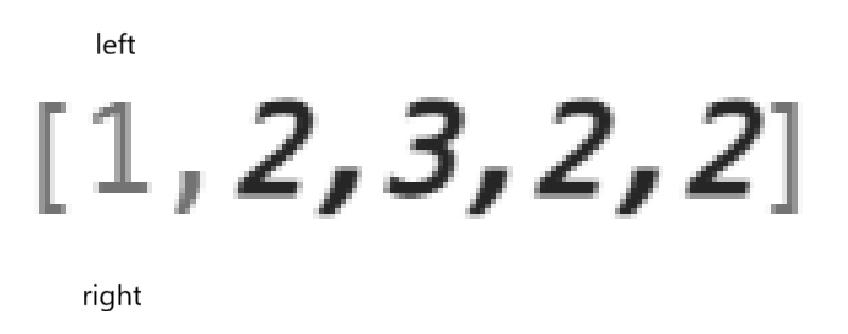
我怎么知道现在装了几种水果呢？

哈希表呗。

right移动情况是什么呢？

有点小讲究，因为它肯定不断右移，将遍历到的元素先入哈希表，入了以后检测哈希表中有几种类型的水果。

或者这样吧，如果还遍历哈希表太挫了，用个变量，多加一种水果就++。

left的移动情况是什么呢？

能动left说明再入哈希表，种类就是3了，这个时候记录一下len，len是维护的区间的长度；

记录完len，left不能只++，因为样例我看了不止一个：

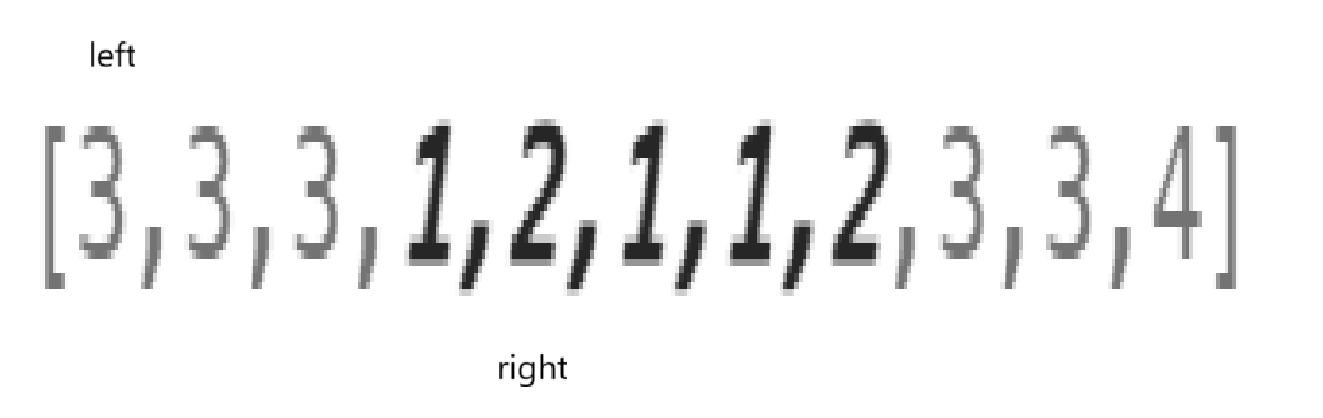
这种情况只++left的话，那么能够得到的也就是子区间，所以应当是啥时候把left调整前占的数从哈希表里清完再停下。

还有个有点小挫的点：

照这么看炸缸了不是，水果种类存哈希表，我哈希表得搞100000，不然不能保证所有样例过，unoredered_set真不想随便用，那玩意开销也不小，底层哈希桶嘛。

反正空间复杂度还是O(1)就完了。

class Solution {
public:int totalFruit(vector<int>& fruits) {int left = 0;int right = 0;int len = 0;int kinds = 0;int hash[100000] = { 0 };while (right < fruits.size()){if (hash[fruits[right]] == 0)++kinds;hash[fruits[right]]++;++right;if (kinds > 2){len = len >= right - left - 1 ? len : right - left - 1;while (kinds > 2){--hash[fruits[left]];if (hash[fruits[left]] == 0)--kinds;++left;}}}if (kinds == 2)len = len >= right - left ? len : right - left;if (kinds == 3 && (hash[fruits[right - 1]] != hash[fruits[right - 2]]))len = len >= right - 1 - left ? len : right - 1 - left;return len;}
};

我连边界都考虑了，分别是这两种：

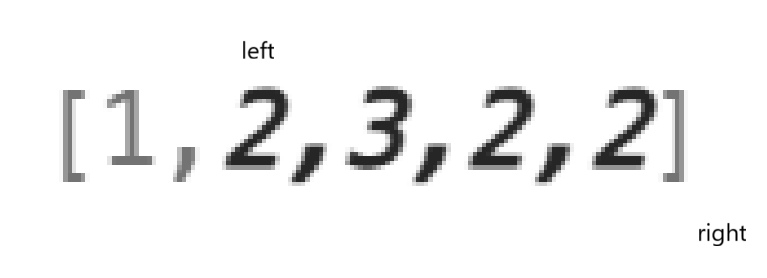
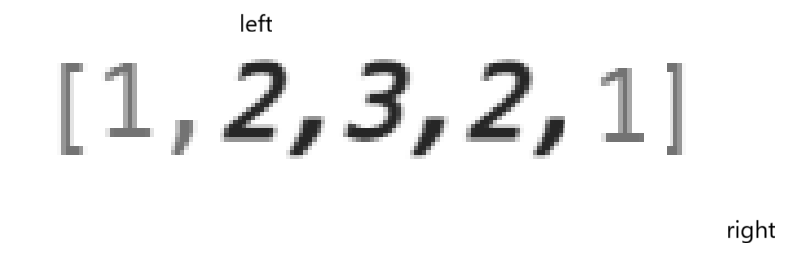
结果只有一种果树的例子还给我上了一课：

class Solution {
public:int totalFruit(vector<int>& fruits) {int left = 0;int right = 0;int len = 0;int kinds = 0;int hash[100000] = { 0 };while (right < fruits.size()){if (hash[fruits[right]] == 0)++kinds;hash[fruits[right]]++;++right;if (kinds > 2){len = len >= right - left - 1 ? len : right - left - 1;while (kinds > 2){--hash[fruits[left]];if (hash[fruits[left]] == 0)--kinds;++left;}}}if (kinds == 1)return fruits.size();if (kinds == 2)len = len >= right - left ? len : right - left;if (kinds == 3 && (hash[fruits[right - 1]] != hash[fruits[right - 2]]))len = len >= right - 1 - left ? len : right - 1 - left;return len;}
};

多补一个判断，如果全部一样的话怎么办。。

六、找到字符串中所有字母异位词

看这个玩意没啥用，太抽象，看个例子：

等于啥叫异位词呢？

如果给的是abc

要求你返回：

abc acb bac bca cab cba

这些的下标。

并且由第二个例子：

只要能找到，重复不重复人家不在乎，只要你找的是就行。

现在上来第一个问题就很清楚了，你怎么确认ab和ba是异位词呢？

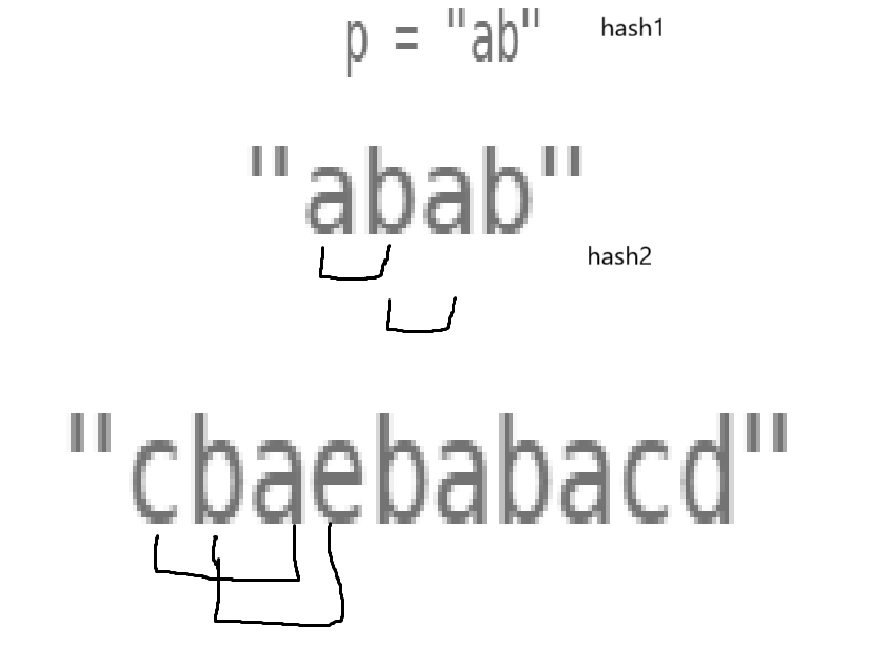
稍微画一画图发现，维护的是一个与p等长的一个区间，比较方便的办法就是把p里面所有元素甩到哈希表里面，到时候遍历的时候，把遍历的元素也甩哈希表里面，对照俩哈希表一样不一样即可。

并且可以发现一个小那啥吧，省事的，就是从上图第一个举例到第二个举例，实际上是在哈希表里去掉当前left所指向元素，++left和++right，入哈希表，这样的话不用每次更新left都得重新搞right，只要维护好区间长度就可以。

很明显，啥时候right越界了就结束了。

class Solution {
public:bool check(int* hash1, int* hash2){for (int i = 0; i < 26; i++)if (hash1[i] != hash2[i])return false;return true;}vector<int> findAnagrams(string s, string p) {int left = 0;int right = p.size() - 1;int hash1[26] = { 0 };for (auto& e : p){++hash1[e - 'a'];}int hash2[26] = { 0 };for (int i = 0; i < p.size(); i++){++hash2[s[i] - 'a'];}vector<int> v;while (right < s.size()){if (check(hash1, hash2))v.push_back(left);--hash2[s[left++] - 'a'];++right;if (right < s.size())++hash2[s[right] - 'a'];elsebreak;}return v;}
};

写出来稍微测试一下倒是过了，但是：

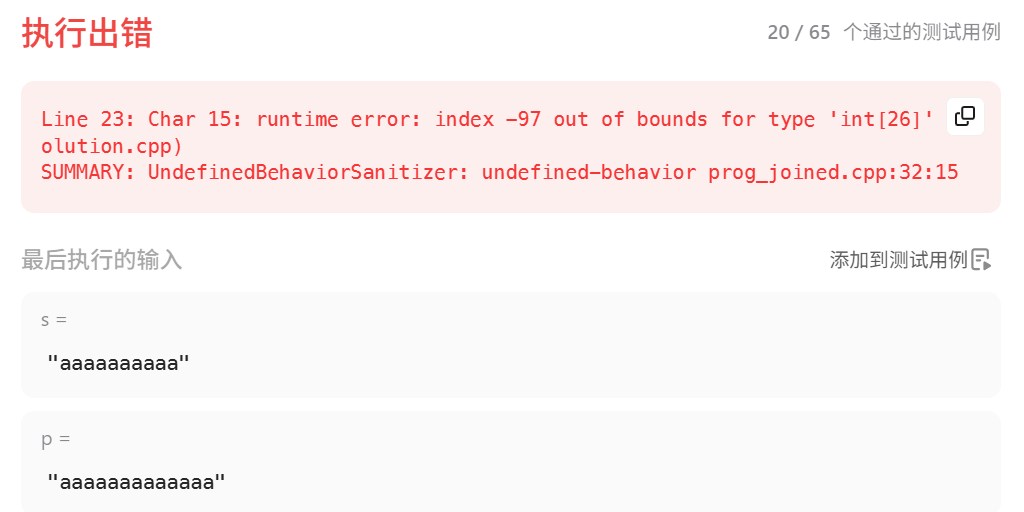
要是p根本就比s长，根本没必要检查了。

所以再正式开始前，最开头最开头，先搞个这个的拦截：

class Solution {
public:bool check(int* hash1, int* hash2){for (int i = 0; i < 26; i++)if (hash1[i] != hash2[i])return false;return true;}vector<int> findAnagrams(string s, string p) {if(s.size() < p.size())return vector<int>();int left = 0;int right = p.size() - 1;int hash1[26] = { 0 };for (auto& e : p){++hash1[e - 'a'];}int hash2[26] = { 0 };for (int i = 0; i < p.size(); i++){++hash2[s[i] - 'a'];}vector<int> v;while (right < s.size()){if (check(hash1, hash2))v.push_back(left);--hash2[s[left++] - 'a'];++right;if (right < s.size())++hash2[s[right] - 'a'];elsebreak;}return v;}
};

其实我老没招了，他为了让我意识到，确实我没考虑到极端情况，在题目里根本只口不提任何如果，根本不存在返回啥，我就蒙一蒙返回了一个匿名vector，然后通过了，说不清楚还有这边界，太抽象了。

七、串联所有单词的子串

30. 串联所有单词的子串 - 力扣（LeetCode）

看下面的例子就能理解了，大致意思就是你在s中要找words中所有字符串的排列组合，返回下标。

思路

看典例其实官方给我们提示了：

所以暴力解法呼之欲出了，就是这样：

用一个固定长度的区间去遍历即可。

由暴力解法其实很容易能看出来如何优化，那就是，既然words里所有字符串都不以a r开头，那么我们上述以a了r了这些暴力根本没必要枚举。

大致上这么枚举就可以了，问题是这玩意咋实现呢？

一步一步从暴力解法看看到底有哪些能够优化的。

不过还有个没在上面显示，那就是区间右端的right如何移动的？

其实很简单，不用太在意细节，因为很明显题目的意思已经给出来了：

left如果是0，words所有单词拼接起来假如是个sum，那么其实right就是0 + sum。

以后每次改变left变right就行，而且容易知道，每次我们都是++left，所以应该也是++right，如果写while循环，那么条件一定是right < s.size()。

暴力

大致上这么写就ok。

class Solution {
public:bool isinside(string& s, int begin, int len){string word;for (int i = begin; i < begin + len; i++){word += s[i];}return hash1.count(word);}//写check的时候保证至少长度是够sum的bool check(string& s, int begin, int len, int sum){unordered_map<string, int> hash2;//先入哈希表for (int i = begin; i < begin + sum; i += len){string str;for (int j = i; j < i + len; j++){str += s[j];}++hash2[str];}//遍历对比for (auto& [k, v] : hash1){if (hash2[k] != v)return false;}return true;}vector<int> findSubstring(string s, vector<string>& words) {int len = words[0].size();int num = words.size();int sum = len * num;int left = 0;int right = sum;vector<int> v;if (s.size() < sum)return v;//如果合法还是进hash1for (auto& e : words){++hash1[e];}while (right < s.size()){if (isinside(s, left, len)){if (check(s, left, len, sum)){v.push_back(left);++left;++right;}else{++left;++right;}}else{++left;++right;}}if(isinside(s, left, len)&&check(s, left, len, sum))v.push_back(left);return v;}
private:unordered_map<string, int> hash1;
};

优化

咋想咋写就是这么写的，但是我总感觉时间复杂度还是太高了。

既然left和right都只向右移动具有一定的单调性，那么我想知道，到底我应该怎么样写，才能写出来滑动窗口呢？毕竟上面的代码仅仅是一点一点暴力。

我再研究了研究，就从这里下手：

啥意思呢？

你会发现红绿蓝开始，每次sum个为一个区间，去遍历，它们不会重，但是如果bar开头，又从foo开头，其实已经重了。

等于left的起始位置其实只有从开头开始的len个位置，len为words中单个单词长度在典例中即为：

所以相当于要做len次查找，想要以滑动窗口的方式，应当是进窗口、判断、出窗口、更新这几个点的有机统一，我是这么做的：

以单词为单位，每次将right向后移动len个长度，并且将此时的单词入哈希表：

倒是有个小问题，我怎么知道什么时候所选单词跟words里所有单词长度完全相同呢？

所以还得搞一个count变量，专门记录容器里到底有几个单词，这么做主要是也考虑到了更新，因为滑动窗口最开始肯定是：

一检测，哦，我现在遍历的哈希表有俩单词了，words里也就俩单词，那就判断，符合要求就记录；不符合要求就是出前面的那一个单词，再往后入一个单词，问题就又来了，我怎么知道我上次记录的是哪一个呢？

一想也想到了，等到啥时候遍历到的单词跟words里的单词一样的时候，right - sum其实是本次遍历的起始位置，这个时候，把

起始位置往后数len个字符给它薅出来，然后让哈希表去除掉，之后继续让right往后入一个单词不就完了，标准滑动窗口做法。

class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {unordered_map<string, int> hash1;unordered_map<string, int> hash2;int len = words[0].size();int num = words.size();int sum = len * num;vector<int> v;if (s.size() < sum)return v;for (auto& e : words)++hash1[e];for (int i = 0; i < len; ++i){for (int left = i, right = i + len, count = 0; right <= s.size(); right += len){++hash2[s.substr(right - len, len)];++count;if (count == num){int flag = 1;for (auto& [k, v] : hash1){if (hash2[k] != v){flag = 0;break;}}if (flag)v.push_back(right - sum);--hash2[s.substr(right - sum, len)];--count;}}hash2.clear();}return v;}
};

最重要的逻辑还是for循环，我们分析出来一共进行len次left起始位置即可；

剩下其实for循环进行的是标准的滑动窗口，right的位置进一个单词，判断以后把最开始的单词出了，下次判断前再根据right位置进一个单词。

时间复杂度好多了。

八、最小覆盖子串

76. 最小覆盖子串 - 力扣（LeetCode）

还是找子串，那就还是用双指针看看咋暴力，研究透暴力再优化暴力算法：

思路

做了这么多题了，其实多少有点经验了：

• 定left走right：不难发现只要找到第一个更好覆盖t字符串的子串以后，其实right指针已经不用再移动了，因为再移会使找到的子串长度变大，这不是我们理想的结果，所以没必要枚举了。比如最上面那一次枚举，会发现再移也不会作为正确答案，这个时候记录一下起始位置和长度即可
• right依旧不用回到left的位置，right站着不动，移left即可

我们甚至可以画一个一般图：

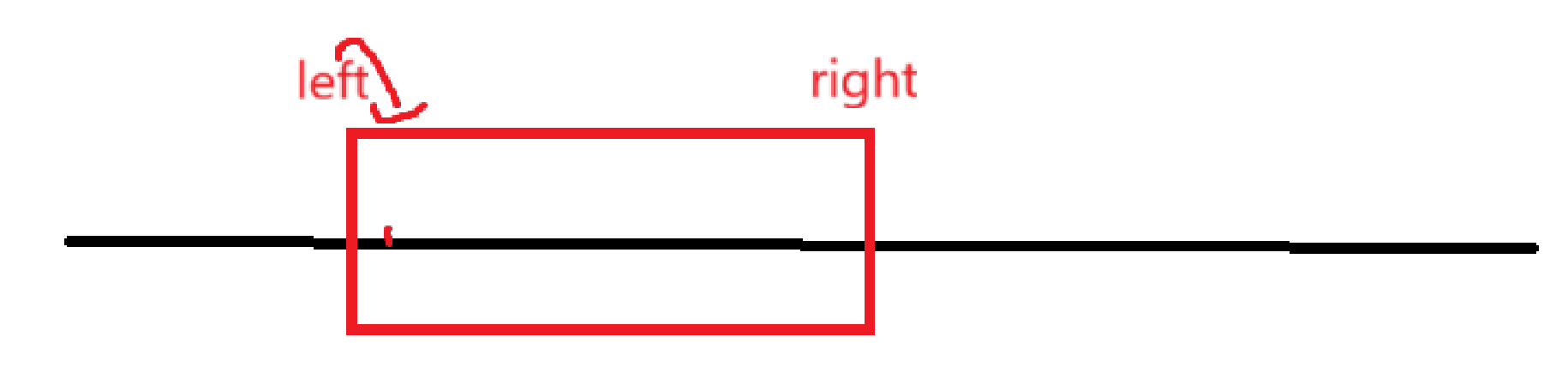
不难发现，刚刚记录过一个区间以后，你肯定是直接++left，这个时候如果令right = left，重新开始遍历，到时候最少right也得移动到当前图上位置才能符合要求，因为我们定left走right一定是刚刚好使得覆盖才停止，图上right包含的最后一个字符是关键。

• 更新left：按照暴力肯定是直接++left，并且在保持right不动的情况下再右移right去寻找合适的区间，找到符合条件的区间后千万别急：从我们图上这么多条线其实还是能看出来，如果left所站位置不是t中的有效字符，其实根本没必要站，直接++即可，看个枚举：

其实left站在D，站在O都没有站到有效字符B短，也就是说，更新结果前检查left所站位置

• 上面这个图你还可以继续枚举缩小子串长度：

当前枚举下，定right，更新前要检查left，一直移移移，碰见不是t中字符右移刚说过，但是如果碰到t中字符呢？难道就不动了吗？

其实当left站到B的位置，可以看到此次遍历所呈现区间B >= t中B个数，left完全可以继续右移，直到碰到t中有效字符C，这个时候经检测区间内C == t中C个数，这次真的不能再移了。

至于如何知道当前区间是否覆盖t中字符串，依旧是哈希表，当然，这次不需要用STL里的容器了，有一条件：

不用废话，hash[128]就够用了。

优化

写check函数我肯定得考虑一下我现在的逻辑嘛，大致上肯定是从遍历t比较记录在hash1和hash2的值，遍历一个个的值真是麻烦啊，我的老天爷，主要每次循环都得走一遍check，太抽象了，你要问我为啥以前就老老实实的遍历，因为以前是两个哈希表元素必须完全相同，现在不老一样：

搞一个小变量sort：

class Solution {
public:string minWindow(string s, string t) {if (s.size() < t.size())return "";int left = 0;int right = 0;int pos = 0;int len = 0;int hash1[128] = { 0 };int count = 0;//记录种类//入hash1for (auto& ch : t)if (!hash1[ch - 'A']++)++count;int sort = 0;int hash2[128] = { 0 };while (right < s.size()){if (sort < count){if (++hash2[s[right] - 'A'] == hash1[s[right] - 'A'])++sort;++right;}else{//保证当前遍历最短while ((hash1[s[left] - 'A'] == 0) || hash2[s[left] - 'A'] > hash1[s[left] - 'A'])--hash2[s[left++] - 'A'];if (len == 0 || len > right - left){pos = left;len = right - left;}//到这left指向的一定是刚好==t中字符串的字符--hash2[s[left++] - 'A'];--sort;}}//边界处理while (left < right && (hash1[s[left] - 'A'] == 0 || hash2[s[left] - 'A'] > hash1[s[left] - 'A']))--hash2[s[left++] - 'A'];if (sort == count && (len == 0 || len > right - left)){len = right - left;pos = left;}return s.substr(pos, len);}
};

我的思路核心就是这里：

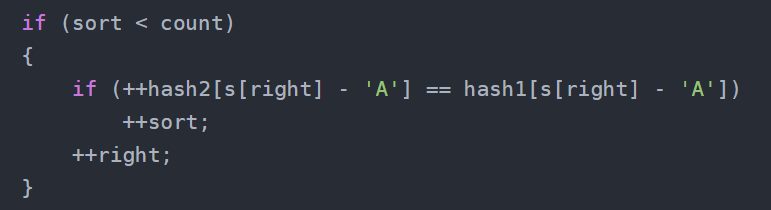
因为这里也不是说，俩哈希表内容必须完全一样，只要覆盖住t即可，所以用sort记录，当你想要入一个字符到hash2，并且这玩意在hash1里有，++以后刚好相等，则当前维护的区间，这个字符肯定符合题目要求，即覆盖到t的字符串。

啥时候sort跟count相等，说明已经覆盖到了，该更新了。

至于这里：

作用其实就是这个优化：

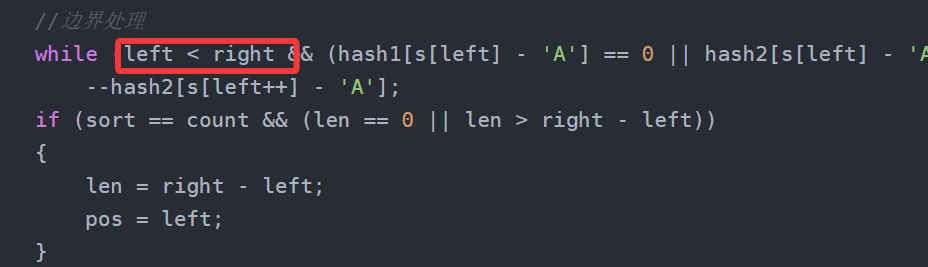
边界处理的时候加了个left < right是因为当时提交的时候碰见一个：

s = "b";

t = "a";

应该是这个例子了，你拿这个例子走读代码去，你会发现越界，所以预防一下。

效率还行。