机器学习--KNN算法中的距离、范数、正则化

一、KNN算法（K最邻进分类算法）

用距离最近的一类来预测未知的类别，到底属于哪个类

例子：假设统计了几个人的身高数据，并且知道这几个人的性别，这时候来了一个人：知道身高但不知道性别，现在来预测一下这个人的性别

通过距离来进行算法分类:

在一维数轴上，找到每个人和新来的这个人的身高，通过寻找3个身高与新人相差最小的人（k=3)来预测新来的人到底是男性还是女性。计算每个人与新来的人的身高差（出现负数预测不靠谱），则将身高差先平方后开方，其中身高差最小的三个人也就是与新来的人距离最近的人，其中三个人中有两个人为女性，则预测新来的人为女性。

若在数据中增加一个体重数据，则建立二维平面图，同上根据距离进行算法分类

若在数据中再增加一个腰维数据，则建立平面直角坐标系，同上根据距离进行算法分类

二、计算距离的几种距离公式

1.曼哈顿距离

常用在汽车导航（比较两个目的地的距离哪个更长），计算机视觉领域（识别两个相似的图像或者物体）

2.欧氏距离

常用在推荐算法，欺诈检测，图像识别当中

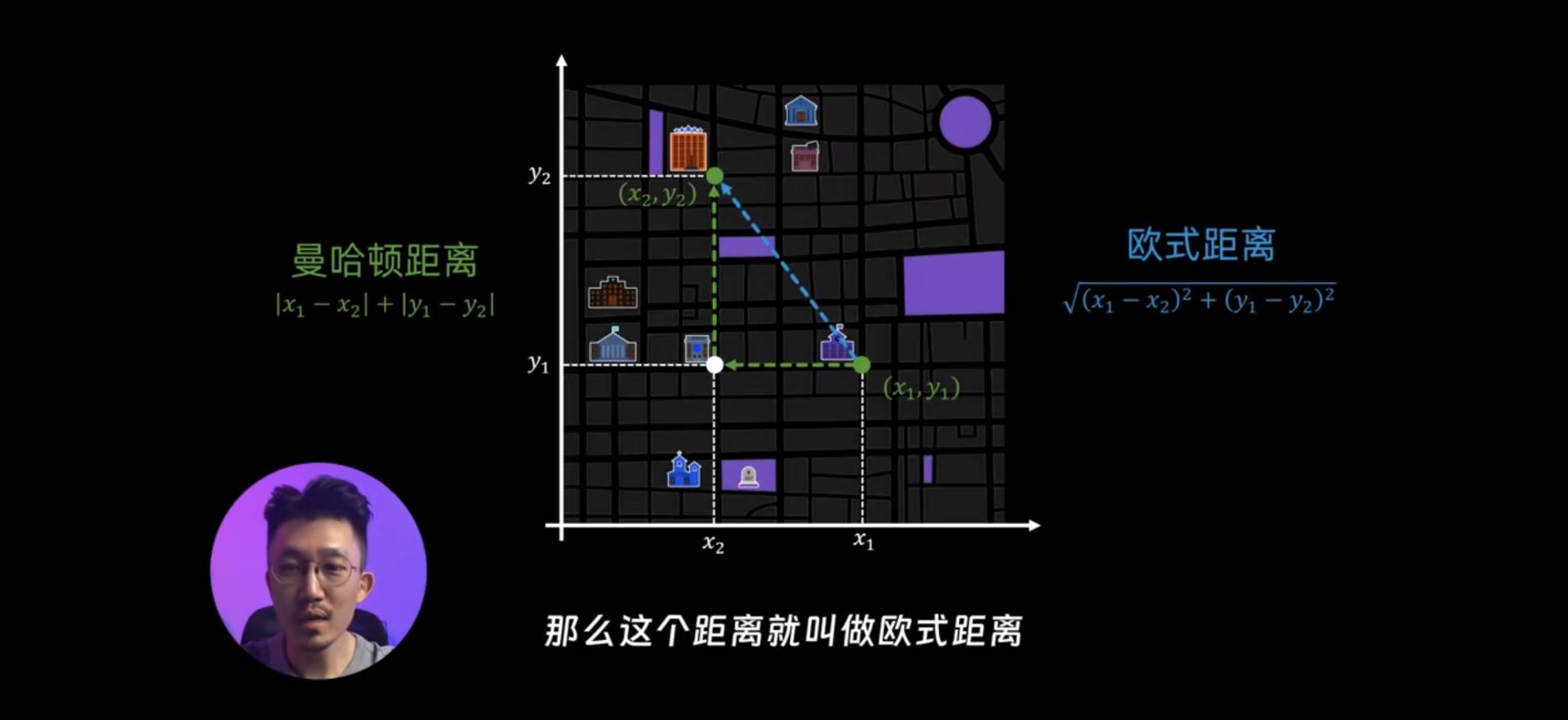
3.切比雪夫距离（国王距离）

计算两个数据点之间任意维度上差的最大距离

4.闵可夫斯基距离（距离度量的统一框架）

三、距离，范数，正则化的关系

距离：定义在空间上任意两点之间，衡量空间上两点之间的间隔或者差异

范数：计算向量的长度，来衡量一个向量的大小（必须为非负的实数）

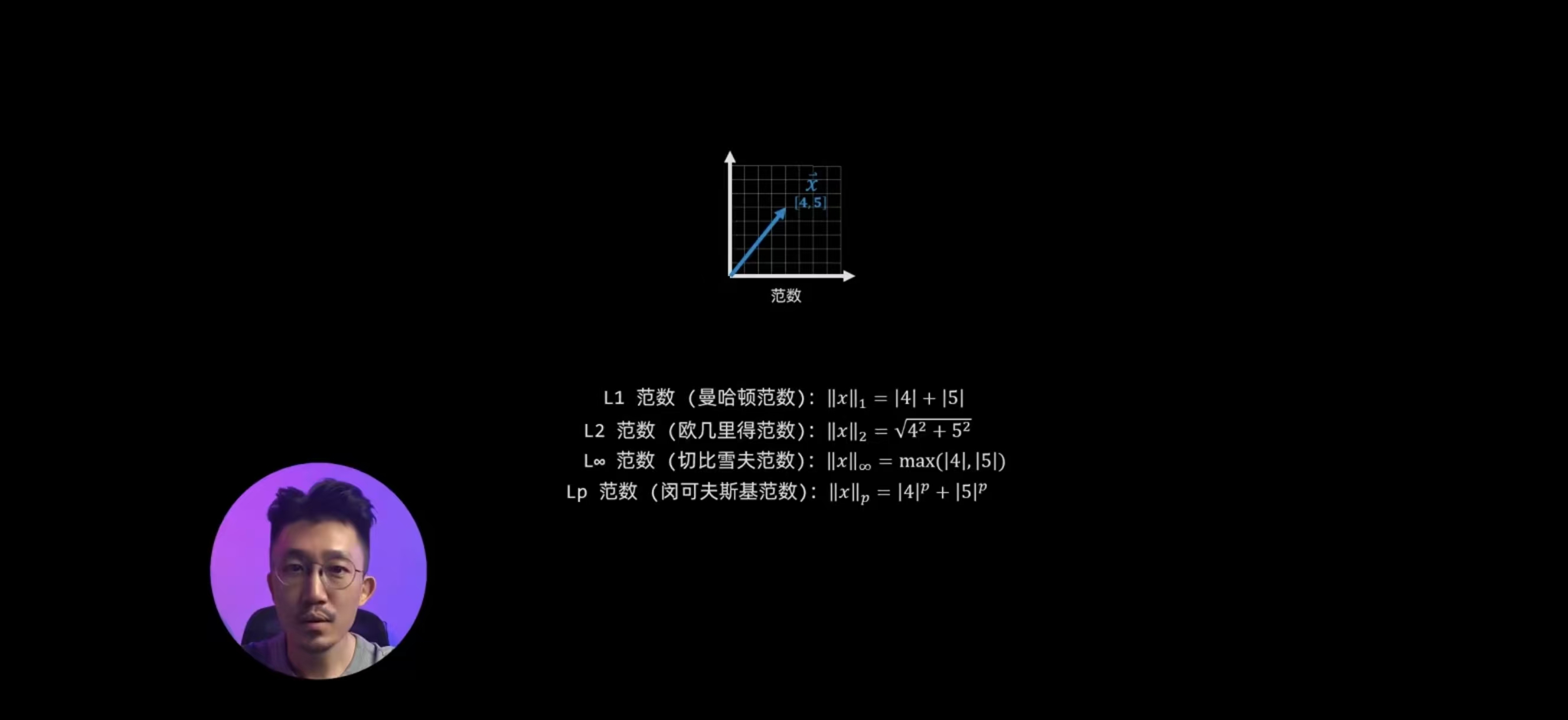
正则化：解决过拟合问题

距离的度量是范数的几何应用，而正则化则是范数的算法约束应用