当前位置： 首页 > news >正文

oj题 ——— 链式二叉树oj题

news 2025/11/13 5:40:54

目录

链式二叉树oj题

相同的树

单值二叉树

对称二叉树

二叉树的前序遍历

另一棵树的子树

二叉树遍历

链式二叉树oj题

相同的树

100. 相同的树 - 力扣（LeetCode）

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

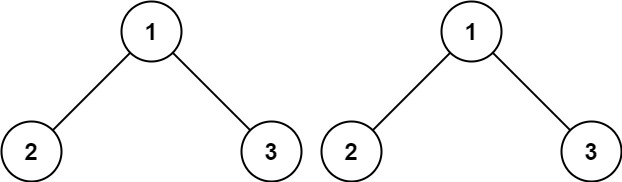
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

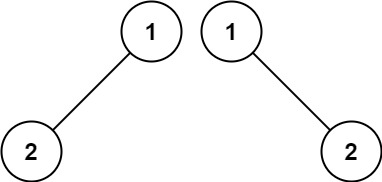
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

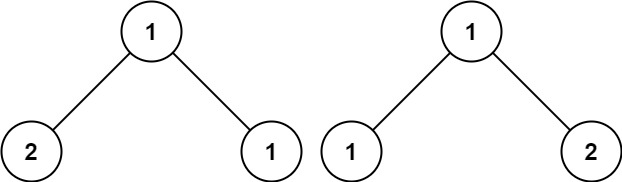
输入：p = [1,2,1], q = [1,1,2]
输出：false

代码演示：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if (p == NULL && q == NULL)return true;if (q == NULL || p == NULL)return false;if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

代码解析：

1. 核心判断逻辑：分情况验证节点匹配性

函数isSameTree接收两棵树的根节点p和q，通过以下步骤判断是否相同：

情况 1：两个节点都为空（p == NULL && q == NULL）→ 返回true

若p和q都是NULL，说明当前位置的 “节点” 在两棵树中都不存在，结构上完全匹配，因此返回true。

  • 例如：两棵树的某个叶子节点的左 / 右子树都为空，此时这部分结构相同。

情况 2：一个节点为空，另一个非空（q == NULL || p == NULL）→ 返回false

若p和q中一个是NULL，另一个不是，说明两棵树在当前位置的结构不匹配（一个有节点，一个没有），直接返回false。

  • 例如：树p的左子树为空，树q的左子树有节点，此时结构不同。

情况 3：两个节点都非空，但值不相等（p->val != q->val）→ 返回false

若p和q都不是NULL，但它们的节点值不同，说明当前节点不匹配，返回false。

  • 例如：树p的当前节点值为2，树q的对应节点值为1，值不匹配。

情况 4：两个节点都非空且值相等 → 递归验证左右子树

若当前节点值相等（p->val == q->val），则需要进一步验证它们的左子树和右子树是否也相同：

  • 递归调用isSameTree(p->left, q->left)：检查左子树是否相同；
  • 递归调用isSameTree(p->right, q->right)：检查右子树是否相同；
  • 只有左子树和右子树都相同（两个递归调用都返回true），整体才返回true（用&&连接结果）。

2. 递归过程：从根到叶逐层验证

整个判断过程是 “自顶向下” 的：

  • 先验证根节点是否匹配；
  • 若根节点匹配，再分别验证左子树的根节点、右子树的根节点；
  • 以此类推，直到所有叶子节点的左右子树（均为NULL）都被验证，确保每一层的结构和值都完全一致。

单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：

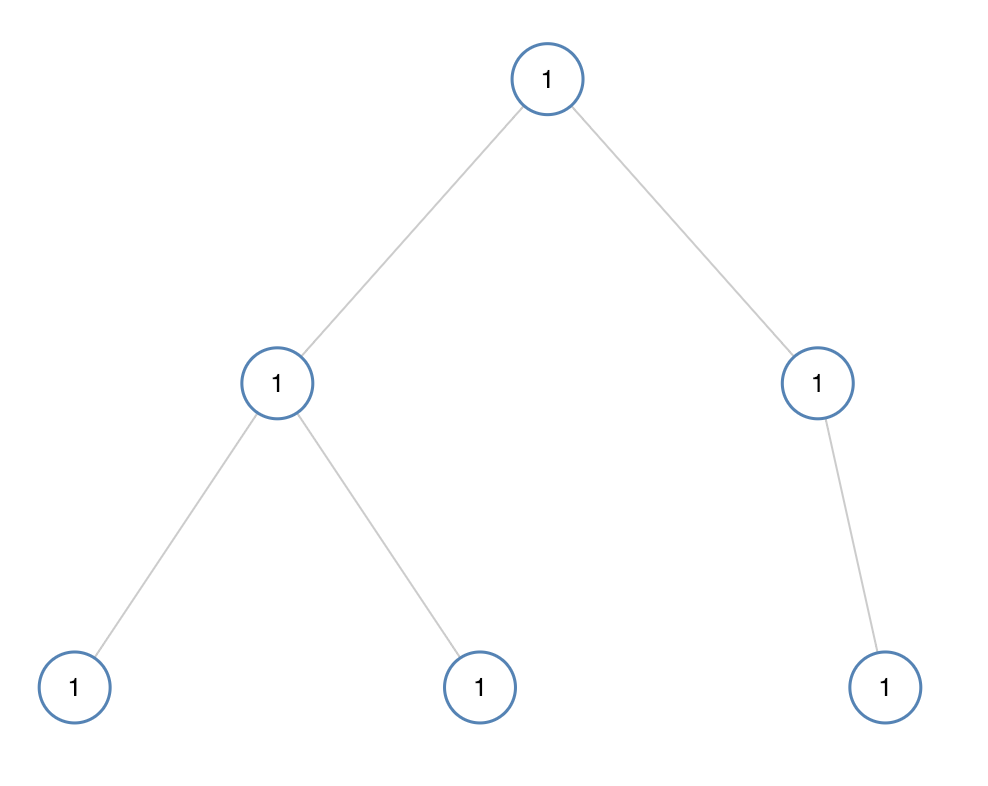
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

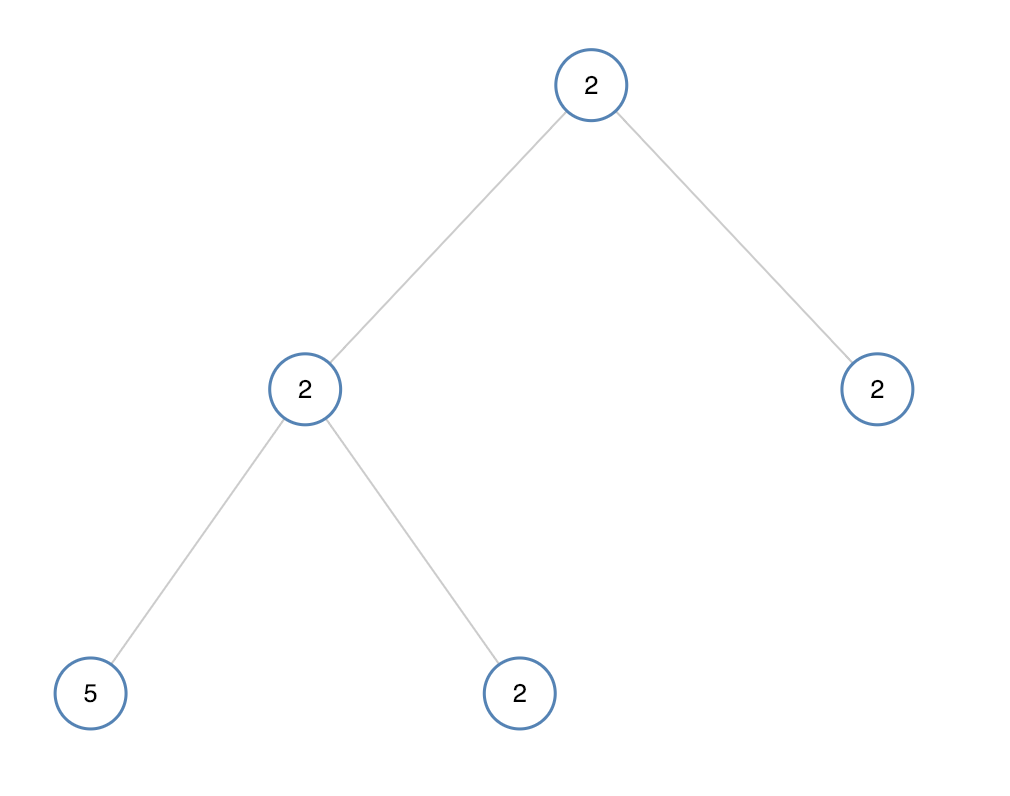
输入：[2,2,2,5,2]
输出：false

代码演示：

bool isUnivalTree(struct TreeNode* root) 
{if (root == NULL)return true;if ((root->left != NULL && root->val != root->left->val) || (root->right != NULL && root->val != root->right->val))return false;return isUnivalTree(root->left) && isUnivalTree(root->right);   
}

代码解析：

1. 边界处理：空树视为单值二叉树

代码开头判断if (root == NULL)，若当前节点为空（如叶子节点的左右子树、空树的根节点），则返回true。

  • 原因：空树没有任何节点，自然不存在 “不同的值”，符合 “单值” 的定义；对于非空树的空孩子节点（如叶子节点的左 / 右子树），也无需检查（没有节点可对比）。

2. 核心判断：当前节点与左右孩子的值是否一致

通过if ((root->left != NULL && root->val != root->left->val) || (root->right != NULL && root->val != root->right->val))判断当前节点是否破坏 “单值性”：

  • 条件拆解：
    • 若左孩子存在（root->left != NULL），且左孩子的值与当前节点值不同（root->val != root->left->val）→ 不符合单值，返回false；
    • 或右孩子存在（root->right != NULL），且右孩子的值与当前节点值不同（root->val != root->right->val）→ 不符合单值，返回false。
  • 作用：直接拦截 “当前节点与子节点值不同” 的情况，避免无效的递归。

3. 递归验证：左右子树是否均为单值二叉树

若当前节点与左右孩子（若存在）的值均一致，则需进一步验证左右子树是否也满足 “所有节点值相同”：

  • 递归调用isUnivalTree(root->left)：检查左子树是否为单值；
  • 递归调用isUnivalTree(root->right)：检查右子树是否为单值；
  • 只有左右子树都为单值二叉树（两个递归调用都返回true），当前树才是单值二叉树（用&&连接结果）。

对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

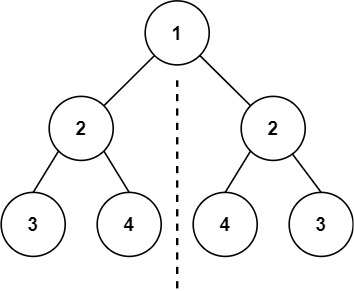
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

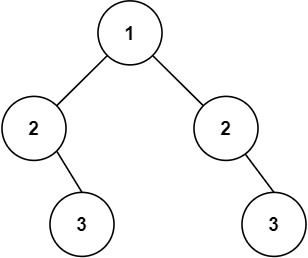
输入：root = [1,2,2,null,3,null,3]
输出：false

代码演示：

bool _isSymmetric(struct TreeNode* leftRoot, struct TreeNode* rightRoot)
{if (leftRoot == NULL && rightRoot == NULL)return true;if (leftRoot == NULL || rightRoot == NULL)return false;if (leftRoot->val != rightRoot->val)return false;return _isSymmetric(leftRoot->left, rightRoot->right) && _isSymmetric(leftRoot->right, rightRoot->left);
}
bool isSymmetric(struct TreeNode* root)
{if (root == NULL)return true;return _isSymmetric(root->left, root->right);
}

代码解析：

1. 主函数isSymmetric：启动对称判断

主函数负责处理根节点的边界情况，并启动对左右子树的镜像判断：

  • 若根节点root为空（空树），直接返回true（空树是轴对称的）；
  • 否则，调用辅助函数_isSymmetric，传入根节点的左子树（root->left）和右子树（root->right），因为 “整棵树轴对称” 等价于 “左子树与右子树互为镜像”。

2. 辅助函数_isSymmetric：核心镜像判断逻辑

辅助函数接收两个节点（leftRoot和rightRoot），判断这两个节点是否为 “镜像对称” 的（即结构相同、对应值相同，且子节点也镜像对称），分四步判断：

步骤 1：两个节点都为空 → 对称

若leftRoot == NULL && rightRoot == NULL，说明两个位置的节点都不存在，结构上对称，返回true。

  • 例如：左子树的某个节点的左孩子为空，右子树对应节点的右孩子也为空，这部分结构对称。

步骤 2：一个节点为空，另一个非空 → 不对称

若leftRoot == NULL || rightRoot == NULL（即一个存在一个不存在），说明两个位置的结构不匹配（一边有节点，一边没有），返回false。

  • 例如：左子树的节点有左孩子，右子树对应节点的右孩子为空，结构不对称。

步骤 3：两个节点都非空，但值不相等 → 不对称

若两个节点都存在（非空），但leftRoot->val != rightRoot->val，说明对应节点的值不匹配，返回false。

  • 例如：左子树的节点值为 3，右子树对应节点值为 4，值不对称。

步骤 4：两个节点都非空且值相等 → 递归判断子节点的镜像关系

若当前节点值相等，需进一步验证它们的子节点是否满足 “镜像对称” 的对应关系：

  • 左子树的左节点（leftRoot->left）需与右子树的右节点（rightRoot->right）对称（左对右）；
  • 左子树的右节点（leftRoot->right）需与右子树的左节点（rightRoot->left）对称（右对左）；
  • 只有这两组子节点都对称（两个递归调用都返回true），当前节点才是镜像对称的（用&&连接结果）。

二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]

输出：[1,2,3]

解释：

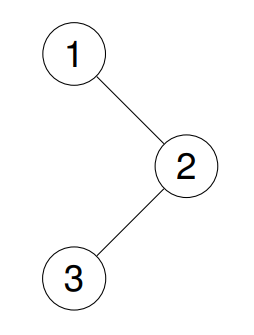
示例 2：

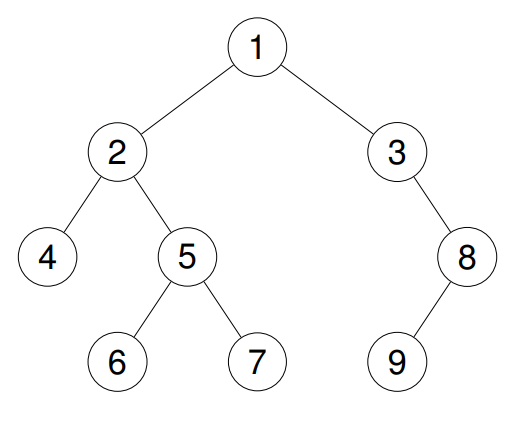
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

代码演示：

int BTreeSize(struct TreeNode* root)
{if (root == NULL)return 0;return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
void _preorderTraversal(struct TreeNode* root, int* PrevOrderArr, int* pi)
{if (root == NULL)return;PrevOrderArr[(*pi)++] = root->val;_preorderTraversal(root->left, PrevOrderArr, pi);_preorderTraversal(root->right, PrevOrderArr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{*returnSize = BTreeSize(root);int* PrevOrderArr = (int*)malloc(sizeof(int) * (*returnSize));if (PrevOrderArr == NULL){perror("preorderTraversal.malloc");return NULL;}int i = 0;_preorderTraversal(root, PrevOrderArr, &i);return PrevOrderArr;
}

代码解析：

1. BTreeSize函数：计算二叉树的节点总数

该函数的作用是统计二叉树中所有节点的数量，为后续分配存储遍历结果的数组提供大小依据，避免数组溢出或空间浪费。

  • 递归逻辑：
    • 若当前节点root为空（root == NULL），返回 0（空树 / 空子树无节点）；
    • 否则，返回 “左子树的节点数”+“右子树的节点数”+1（当前节点本身）。
  • 例如：对于示例 1 的树[1,null,2,3]，左子树为空（0 个节点），右子树有 2 个节点（2 和 3），加上根节点 1，总节点数为0+2+1=3。

2. _preorderTraversal函数：递归执行前序遍历，填充结果数组

该辅助函数负责按照 “根→左→右” 的前序顺序，将节点值存入数组，核心依赖递归实现子树的遍历。

  • 参数说明：
    • root：当前遍历的子树的根节点；
    • PrevOrderArr：存储遍历结果的数组；
    • pi：指向数组当前填充索引的指针（用于在递归中共享同一个索引，确保值按顺序连续存储）。
  • 递归逻辑（前序顺序）：
    1. 若当前节点root为空，直接返回（空子树无需处理）；
    2. 访问根节点：将当前节点值root->val存入数组的PrevOrderArr[*pi]，然后通过(*pi)++将索引后移一位（准备存储下一个值）；
    3. 递归遍历左子树：调用_preorderTraversal(root->left, PrevOrderArr, pi)，处理左子树的所有节点；
    4. 递归遍历右子树：调用_preorderTraversal(root->right, PrevOrderArr, pi)，处理右子树的所有节点。

3. preorderTraversal函数：主函数，统筹遍历流程

该函数是对外的接口，负责协调 “计算节点数→分配数组→启动遍历” 的全流程，并返回最终结果。

  • 步骤分解：
    1. 计算节点总数：通过BTreeSize(root)得到树的节点数，存入*returnSize（用于告诉调用者结果数组的长度）；
    2. 分配结果数组：根据节点数*returnSize，用malloc分配一个 int 类型数组PrevOrderArr，若分配失败（PrevOrderArr == NULL），通过perror提示错误并返回NULL；
    3. 初始化索引：定义int i = 0作为数组的初始填充索引（从 0 开始）；
    4. 启动遍历：调用_preorderTraversal(root, PrevOrderArr, &i)，将遍历结果存入数组；
    5. 返回结果：返回填充好的数组PrevOrderArr。

另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

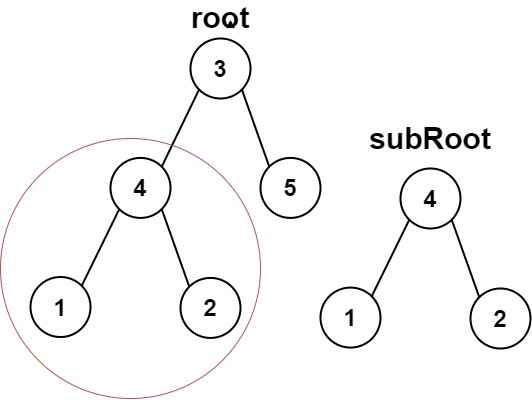
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

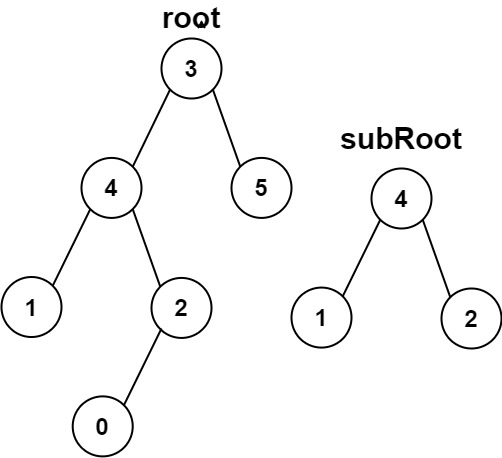
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

代码演示：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if (p == NULL && q == NULL)return true;if (q == NULL || p == NULL)return false;if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{if (root == NULL)return false;if (isSameTree(root, subRoot))return true;return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

代码解析：

1. 辅助函数isSameTree：判断两棵树是否完全相同

该函数是检验子树的基础工具，作用是判断以p和q为根的两棵树是否 “结构相同且对应节点值相同”，逻辑与之前判断相同二叉树一致：

  • 若p和q都为空（p == NULL && q == NULL）→ 相同，返回true；
  • 若一个为空一个非空（p == NULL || q == NULL）→ 结构不同，返回false；
  • 若节点值不同（p->val != q->val）→ 值不匹配，返回false；
  • 否则递归判断左子树（p->left与q->left）和右子树（p->right与q->right），两者都相同才返回true。

2. 主函数isSubtree：检验root中是否包含subRoot作为子树

核心思路是：遍历root的每个节点，将该节点视为潜在的子树根节点，用isSameTree判断其是否与subRoot完全相同，只要存在一个这样的节点，就返回true。具体逻辑分三步：

步骤 1：边界处理 ——root为空时无匹配子树

若root == NULL（已遍历到root的空子孙节点），说明当前路径上没有可匹配的子树，返回false。

步骤 2：检查当前节点的子树是否与subRoot相同

调用isSameTree(root, subRoot)，判断以当前root为根的子树是否与subRoot完全相同：

  • 若返回true（结构和值都一致），说明找到匹配的子树，直接返回true；
  • 若返回false，则继续检查root的左右子树。

步骤 3：递归检查左右子树是否包含subRoot

若当前节点的子树不匹配，递归检查左子树（isSubtree(root->left, subRoot)）和右子树（isSubtree(root->right, subRoot)）：

  • 只要左子树或右子树中存在与subRoot匹配的子树（两个递归调用有一个返回true），整体就返回true（用||连接结果）；
  • 若左右子树都没有匹配的子树，最终返回false。

二叉树遍历

二叉树遍历_牛客题霸_牛客网

描述

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：

输入包括1行字符串，长度不超过100。

输出描述：

可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

示例1

输入：abc##de#g##f###

输出：c b e g d f a

代码演示：

#include <stdio.h>
#include <stdlib.h>typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BinaryTreeNode;BinaryTreeNode* BuyNode(BTDataType x)
{BinaryTreeNode* newnode = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));if (newnode == NULL){perror("BuyNode.malloc");return NULL;}newnode->data = x;newnode->right = NULL;newnode->left = NULL;return newnode;
}void InOrder(BinaryTreeNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}BinaryTreeNode* ConstructBinaryTree(char* parr, int* i)
{if (parr[*i] == '#'){(*i)++;return NULL;}BinaryTreeNode* node = BuyNode(parr[(*i)++]);node->left = ConstructBinaryTree(parr, i);node->right = ConstructBinaryTree(parr, i);return node;
}int main() 
{char prevArr[100];scanf("%s", prevArr);int i = 0;BinaryTreeNode* root = ConstructBinaryTree(prevArr, &i);InOrder(root);return 0;
}

代码解析：

1. 数据结构定义：二叉树节点

BinaryTreeNode结构体定义了二叉树节点的结构，包含三个成员：

  • data：存储节点的值（字符类型，对应输入字符串中的字母或#）；
  • left：指向左子树的指针；
  • right：指向右子树的指针。

2. BuyNode函数：创建新节点

该函数用于为二叉树创建一个新节点，是构建树的基础工具：

  • 功能：分配内存空间，初始化节点的data为输入值x，并将left和right指针设为NULL（初始无左右子树）；
  • 异常处理：若内存分配失败（malloc返回NULL），通过perror提示错误并返回NULL。

3. InOrder函数：中序遍历并输出

该函数通过递归实现二叉树的中序遍历（左子树→根节点→右子树），并按要求输出结果：

  • 遍历逻辑：
    • 若当前节点root为NULL（空树 / 空子树），直接返回（无需处理）；
    • 先递归遍历左子树（InOrder(root->left)）；
    • 再输出当前节点的data（格式为 “字符 + 空格”，如printf("%c ", root->data)）；
    • 最后递归遍历右子树（InOrder(root->right)）。

4. ConstructBinaryTree函数：根据先序字符串构建二叉树

该函数是核心，通过递归按照先序遍历规则（根→左→右）解析字符串，构建二叉树，其中#代表空节点：

  • 参数说明：
    • parr：输入的先序遍历字符串（如"abc##de#g##f###"）；
    • i：指向当前处理字符串索引的指针（用于在递归中共享同一个索引，确保按顺序解析每个字符）。
  • 构建逻辑：
    1. 若当前字符是#（parr[*i] == '#'）：表示当前位置是 “空节点”，索引i加 1（跳过#），返回NULL；
    2. 若当前字符是字母：
      • 创建新节点（BuyNode(parr[*i])），节点值为当前字符，索引i加 1（移动到下一个字符）；
      • 递归构建左子树（node->left = ConstructBinaryTree(parr, i)），即按先序规则处理当前节点的左孩子；
      • 递归构建右子树（node->right = ConstructBinaryTree(parr, i)），即按先序规则处理当前节点的右孩子；
      • 返回当前节点（作为父节点的左 / 右孩子）。

5. main函数：统筹流程

主函数负责串联 “输入→构建树→遍历输出” 的全流程：

  • 读取输入：用scanf读取先序遍历字符串（存储在prevArr中）；
  • 初始化索引：int i = 0，用于跟踪字符串解析的位置；
  • 构建二叉树：调用ConstructBinaryTree(prevArr, &i)，根据字符串生成二叉树的根节点；
  • 中序遍历输出：调用InOrder(root)，按中序顺序输出节点值（每个字符后带空格）。

http://www.dtcms.com/a/600646.html

相关文章：

  • 数据库项目实战五
  • Python调用Java接口失败(Java日志打印警告：JSON parse error：xxxx)
  • 没有网站如何做SEO推广有用吗怎么不花钱自己开网店
  • ArkTS分布式设计模式浅析
  • 倍福PGV100-F200A-R4-V19使用手册
  • FD2000/4的UEFI编译和烧录文件打包过程记录
  • 微信小程序map自定义气泡customCallout
  • 如何在ubuntu调用exe文件
  • Polar MISC （中）
  • 《理解数据在内存中的存储 --- 解密数据在计算机底层的存储秘密》
  • 兰州网站建设公网站可以换虚拟主机吗
  • 营销型网站建设评价深圳福田住房和建设局网站官网
  • 遍历访问阿里云节点下的所有文件信息并写入excel文件
  • 平台消息推送（go）
  • uniapp集成爱山东获取用户信息
  • Python编程实战 - Python实用工具与库 - 操作Excel：openpyxl / pandas
  • 开展我国电子网站建设wordpress表白
  • Java 在 Excel 中添加或删除批注：Spire.XLS for Java 实践指南
  • uniapp 使用unocss的问题
  • [Linux——Lesson23.线程概念与控制：线程基础]
  • 四大主流浏览器Chrome、Edge、Safari、Firefox内核检测免费工具评测
  • 弱网通话没保障？多网聚合，逐包调度，新技术扫除网络痛点
  • 网站制作公司的网站贵阳网站改版
  • 电脑硬件价格呈现持续上涨趋势及软件优化的必要性
  • Spring集成kafka的最佳方式
  • 设计网站怎么做网业是什么行业
  • RK3588应用分享之国产化系统-开源鸿蒙OpenHarmony
  • RabbitMQ-基础-总结
  • 学习react第二天
  • 【JVS更新日志】低代码、APS排产、物联网、企业计划11.12更新说明！