代码随想录 134.加油站

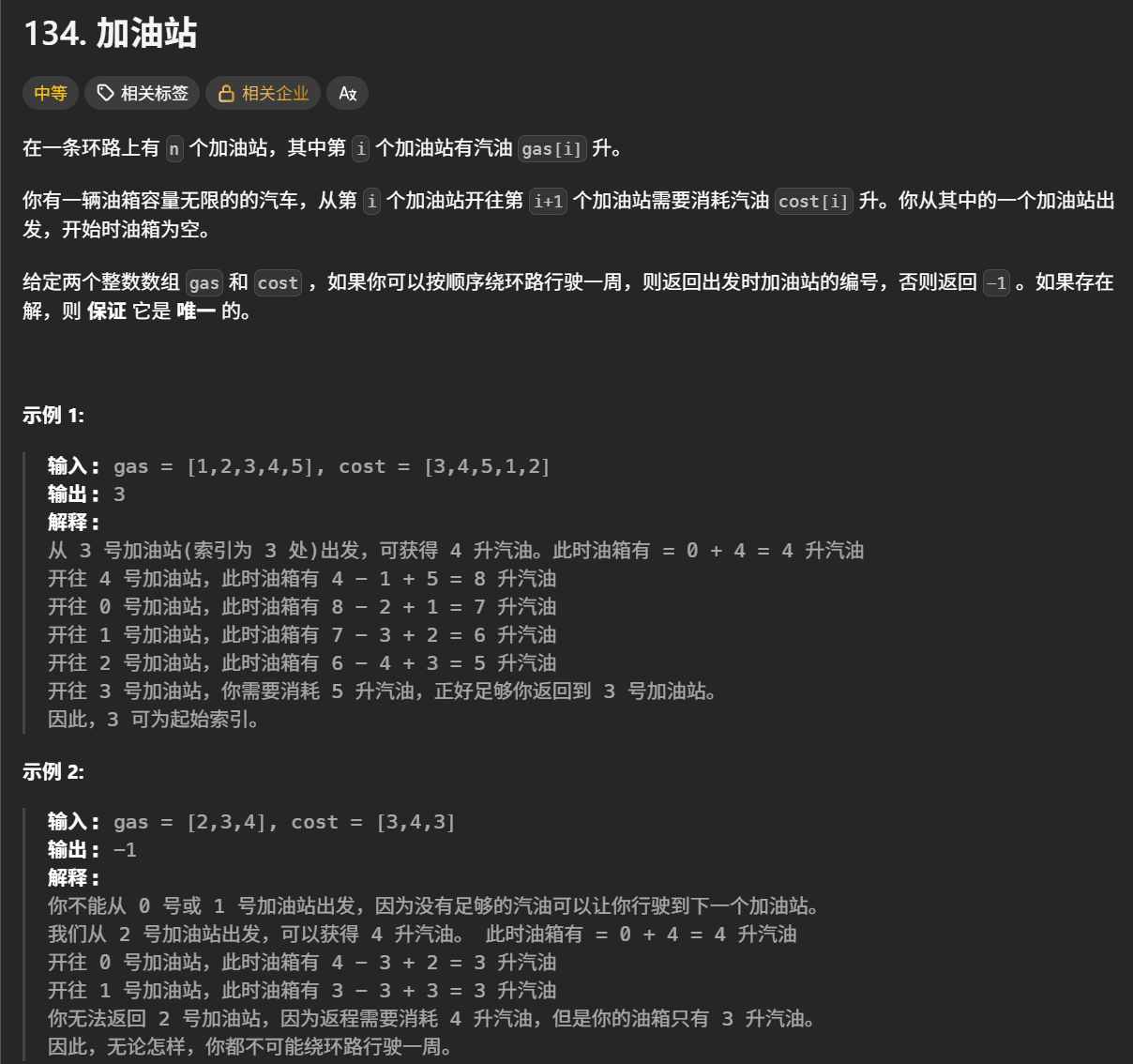
思路：

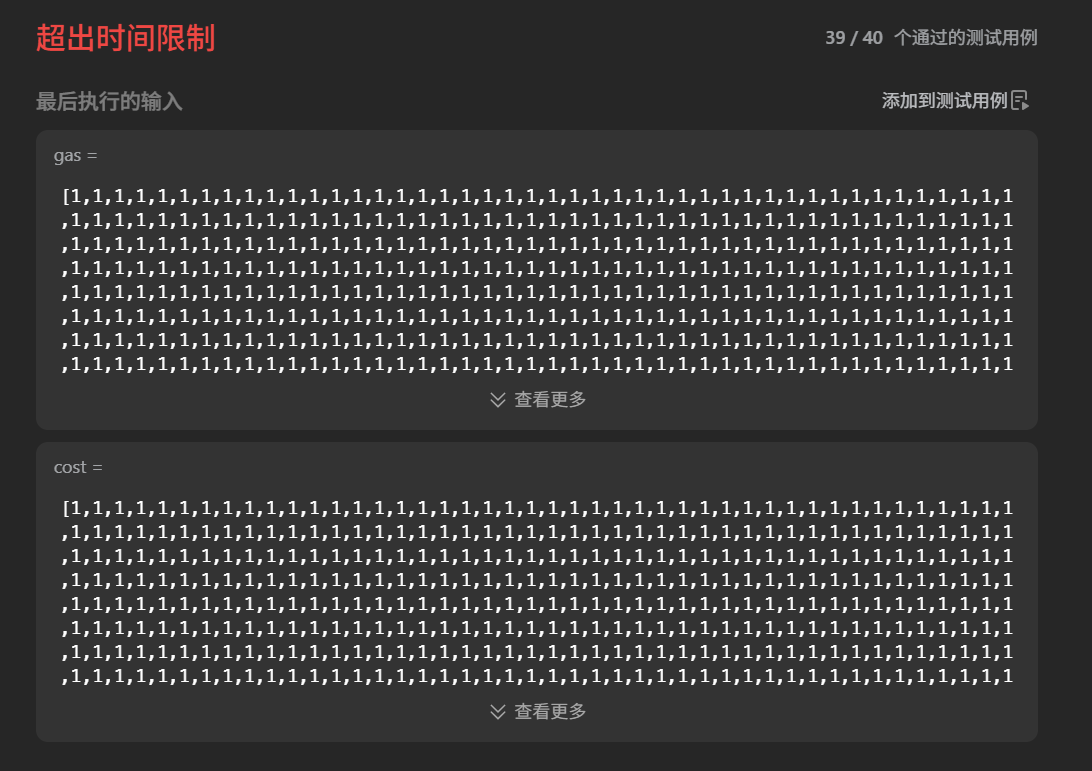
想法：暴力。

暴力的时间复杂度为O（n^2），暴力就是遍历每一个加油站为起点的情况，模拟一圈。如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个点可以作为起点。for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历，在本题遍历中需要借助while循环。

结果：超出时间限制。

方法一：贪心算法。直接从全局进行贪心选择（没有找局部最优，直接从全局最优的角度去考虑，不是严谨的贪心解法）。

（1）情况1：如果gas的总和小于cost的总和，那么无论从哪里出发，一定跑不了一圈。

（2）情况2：rest[i] = gas[i] - cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。

（3）如果累加的最小值是负数，那么汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。

附代码：

class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int tank = 0; //当前油量int totalGas = 0; //总加油量int totalCost = 0; //总油耗int start = 0; //起点for(int i = 0;i < gas.length;i ++){totalGas += gas[i];totalCost += cost[i];tank += gas[i] - cost[i];if(tank < 0){ // tank变为负数意味着在i点没油，从0到i之间无法顺利环路一周tank = 0; //重置tankstart = i + 1; //起点变为i点往后一位}}if(totalCost > totalGas) return -1;return start;}
}

方法二：贪心算法（标准思路，推荐）。

1.如果总油量减去总消耗 >= 0，那么一定可以跑完一圈，说明各个站点的加油站剩油量rest[i]相加一定是 >= 0的。

2.每个加油站的剩油量rest[i] = gas[i] - cost[i]。

3.i从0开始累加rest[i]，和即为curSum，一旦curSum < 0，说明[0,i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，所以起始位置从i + 1算起，再从0计算curSum，如下图所示。

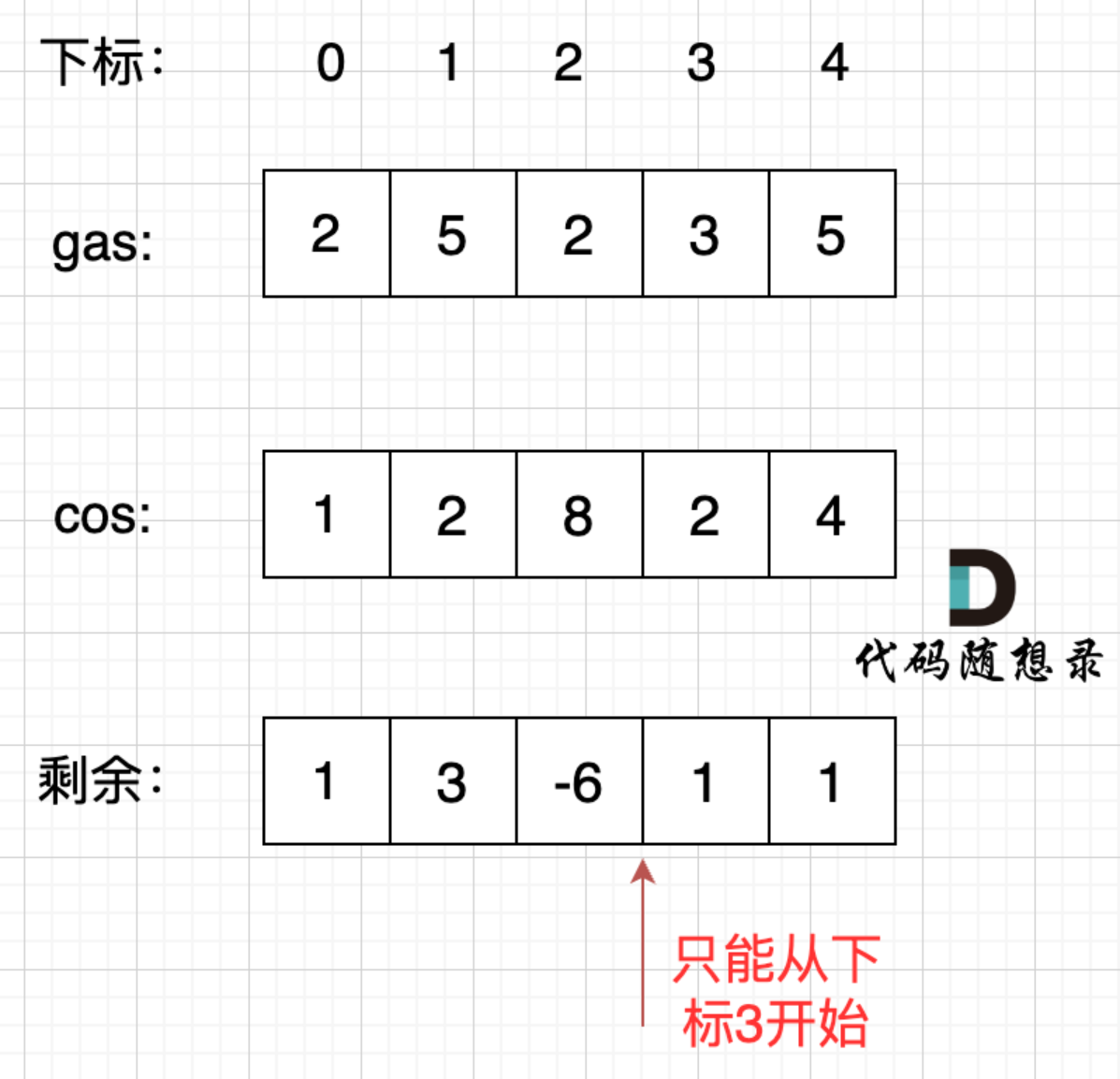
4.起始位置变为i + 1，但i + 1后可能仍可能出现更大的负数。如果出现更大的负数，就继续更新i，那么起始位置又变成了新的i + 1。

5.贪心策略。

（1）局部最优：当前累加的rest[i]的和curSum一旦小于0，起始位置至少要是i + 1，因为从i之前开始一定不行。

（2）全局最优：找到可以跑一圈的起始位置。

（3）局部最优可以推出全局最优，且找不到反例，可以贪心。

附代码：

class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int curSum = 0;int totalSum = 0;int index = 0;for(int i = 0;i < gas.length;i++){curSum += gas[i] - cost[i];totalSum += gas[i] - cost[i];if(curSum < 0){index = (i + 1) % gas.length;curSum = 0;}}if(totalSum < 0){return -1;}return index;}
}