基于Matlab的欧拉法和龙格-库塔法微分方程求解

---

---

前言

我们知道连续系统的特性可以用一组微分方程描述，想要对连续系统进行计算机仿真，就需要对微分方程求解，从而得到每时刻的输出值。目前计算机微分方程求解法采用的都是数值积分法，而欧拉法和龙格-库塔法就是数值积分法的两种常用方法。于是本文将对欧拉法和龙格-库塔法进行一个全面并通俗的讲解。

---

一、数值积分法

n阶连续系统可以用n个一阶微分方程表示，可设其中的一个一阶微分方程为：

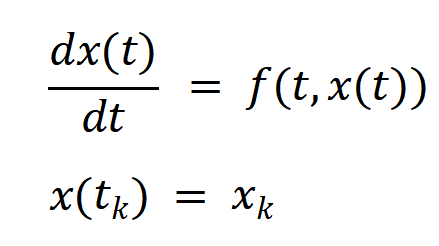
注意其中x(t)的导数是一个关于t和x的二元函数，我们熟悉的系统状态空间表达式正好符合这个形式。

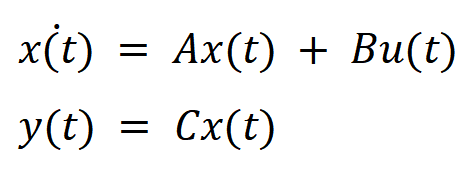
数值积分法就是求出区间[a,b]内若干离散点的近似解。求这种近似解的方法有很多，下面介绍欧拉法和龙格-库塔法。（还不理解这句话含义，下面用具体实例来体会）

二、欧拉法和龙格-库塔法

1.欧拉法

欧拉法是一种很早的数值积分法，精度较低。欧拉法就是将区间[a,b]分成若干小区间，依靠一个初值，通过对小区间内曲线线性化，求出接下来每个小区间的右值。可以看出只要每个区间的步长越小，线性化的拟合程度就越高，计算的结果也就越准确。每个小区间的右值就是若干离散点，用欧拉法求出该离散点的解来代替实际该点的解，那欧拉法求出该离散点的解也就是近似解。
欧拉法的公式如下：

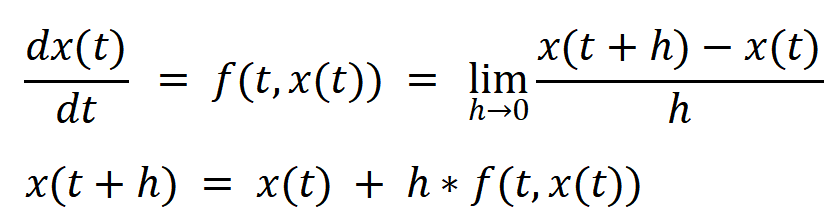
h称为步长，当h越小，那计算的近似解越准确。用系统状态空间表达式实际演算一下：零输出零初始条件，h = 0.1

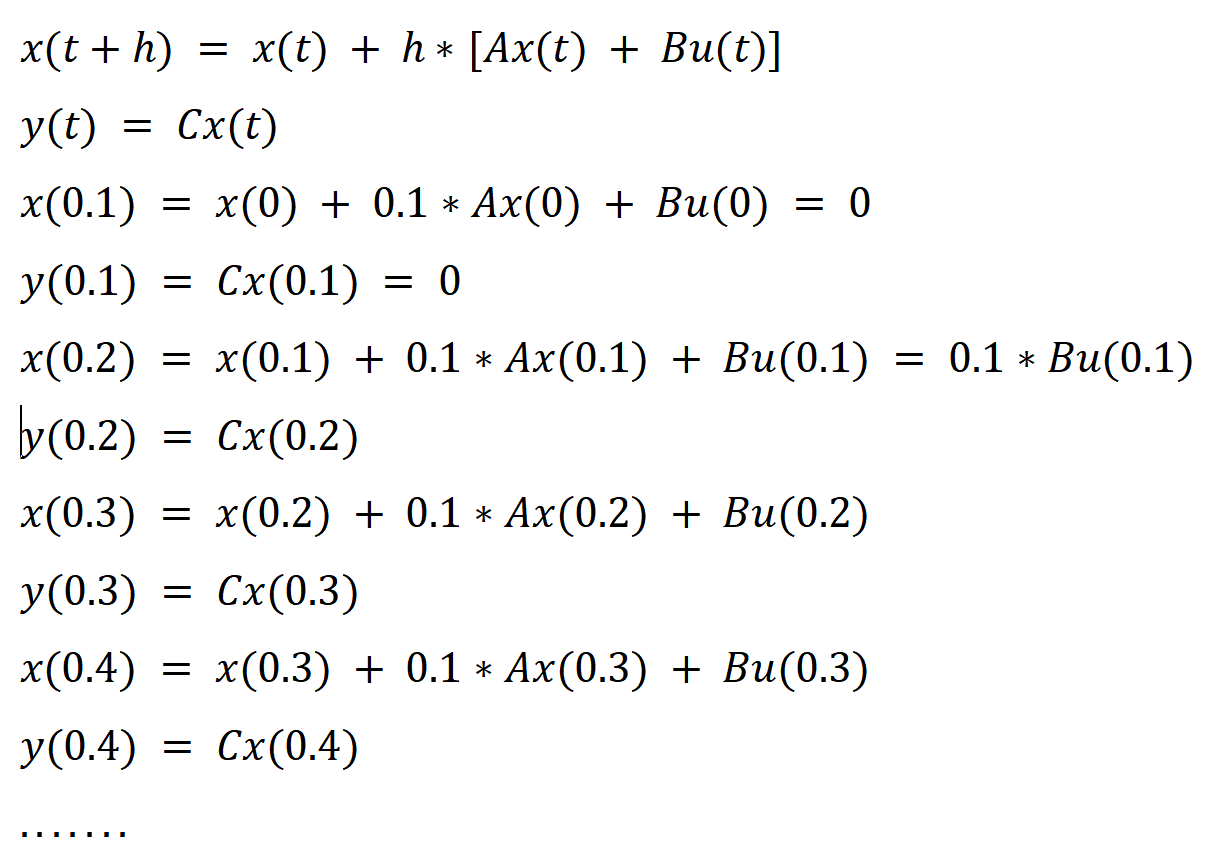
这样每时刻的解就求出来了。在我们看来这种方法已经非常好用了，只要减小h的大小，结果就能更加准确，而且原理清晰，计算简单。但世界上总有天才闪耀，于是有了接下来的龙格-库塔法

2.龙格-库塔法

依旧是将区间[a,b]分成若干小区间，每个区间的右值不再是简单的线性处理求解，而是利用泰勒级数求解。

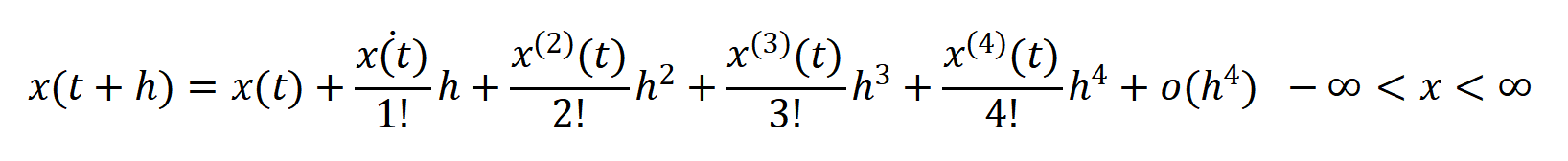
其中h就是每个区间的长度，和欧拉法的h定义是一样的，可以看出在相同h下泰勒级数求出来的x(t+h)比欧拉法求出来的x(t+h)要精准很多。
优点明确了，那缺点很显然，泰勒级数求法计算也太复杂了。不过天才已经想到了解法，那就是用x(t)的线性组合来代替x(t)的各阶导数。接下来以四阶泰勒展开为例来体会一下这种做法。
先直接写出x(t+h)表达式如下，上面说了用x(t)的线性组合来代替x(t)的各阶导数，那K就是x(t)的各阶导数的线性组合，C是系数。四阶龙格-库塔法那只要写到k4就行。

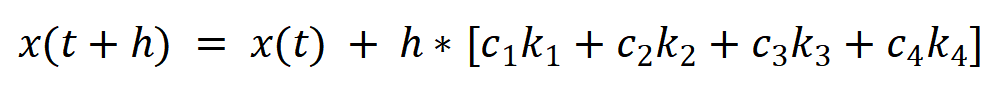
下面直接给出s 阶龙格 - 库塔法的递推公式

去求解证明这个递推公式以本人的浅显数学能力是做不到了，只能尽力给大家解释一下了。
以系统状态空间表达式为例

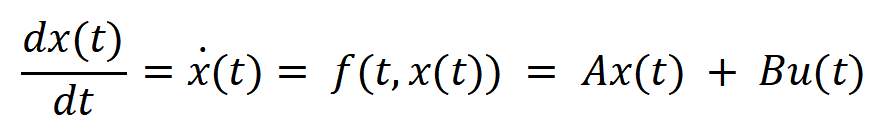
从而求得s 阶龙格 - 库塔法的实例为

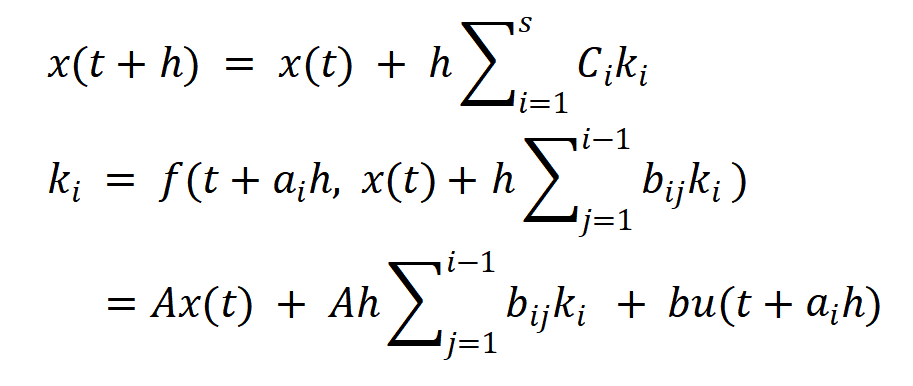
其中的各个系数a，b都需要和泰勒级数比较来确定。各个系数的求解非常复杂，好在这是通式，世界上有人求出来就行了，我等拿着用就好。下面就写出4阶和5阶的计算后的递推公式


可以四阶的表达形式是很简洁的，5阶就开始很复制，6阶计算量就非常大了，下图是一个四阶的龙格-库塔法的图像，相当于一个小区间里再分为4个小区间，每个区间的右值也就是k，利用复杂计算求得，最终得到的f(k+h)的精度可以说是非常高。

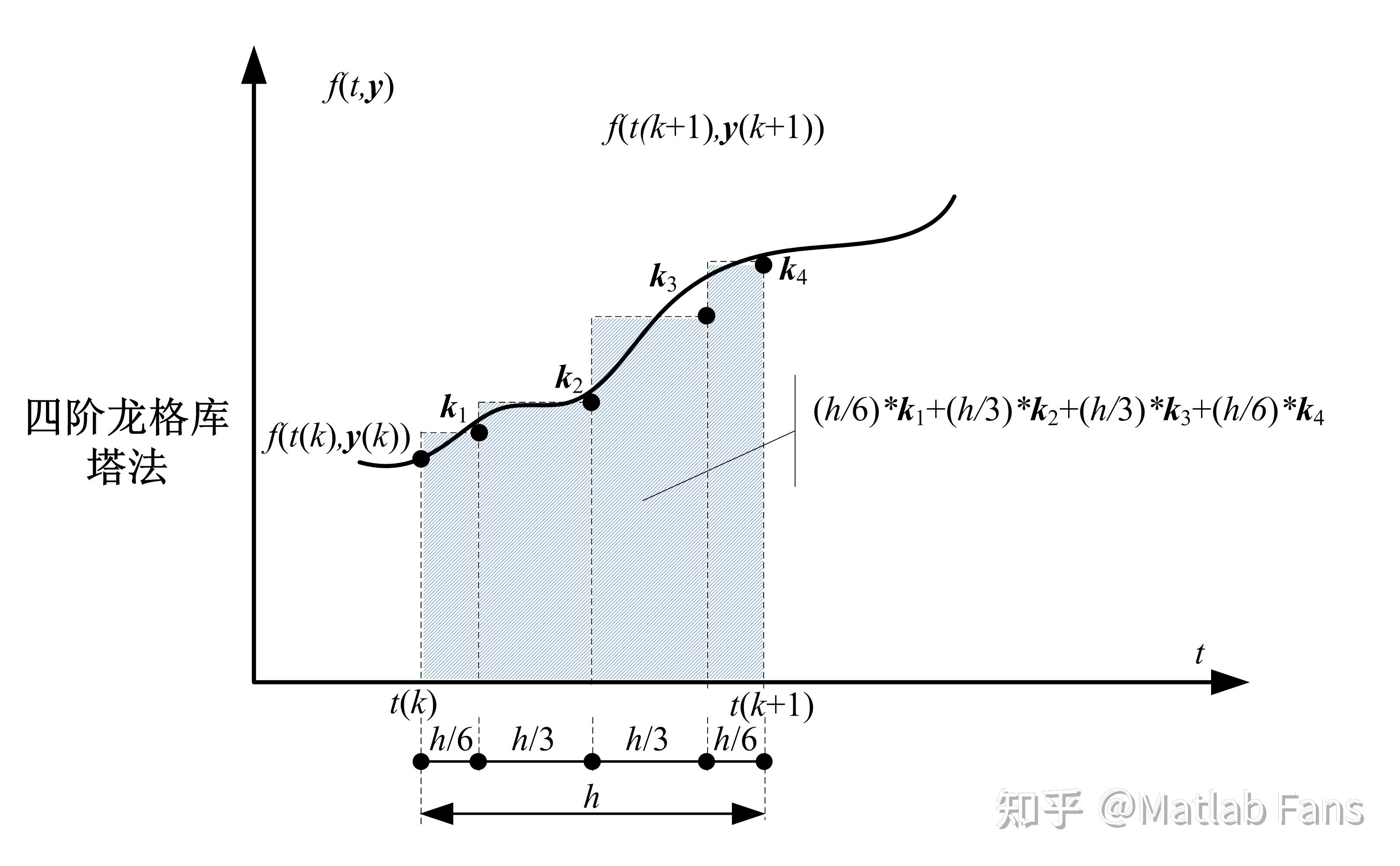
经典 RK5 采用 “6 级 5 阶” 设计，核心原因是显式龙格 - 库塔法的阶数提升受限于系数约束条件和泰勒展开误差消除规则，5 阶精度的显式格式无法用少于 6 个 k 值（级数）实现。这个了解就好

四阶的龙格-库塔法
精度：局部截断误差为o(h⁵)，全局截断误差为o(h⁴)，满足绝大多数工程场景需求。
适用场景：常微分方程初值问题，如动力学仿真、电路暂态分析、种群增长模型等。
高阶的龙格-库塔法
适用场景：RK5 用于对精度要求较高的工程计算（如动力学仿真），RK6 适用于高精度数值模拟（如流体力学、天体运动）。
我们平常用4阶完全足够，

三、Matlab实现

下面将针对一个具体的状态空间表达式，使用matlab用欧拉法、4阶龙格-库塔法和5阶龙格-库塔法求出解值，比较出各方法的差别。
状态空间表达式如下：

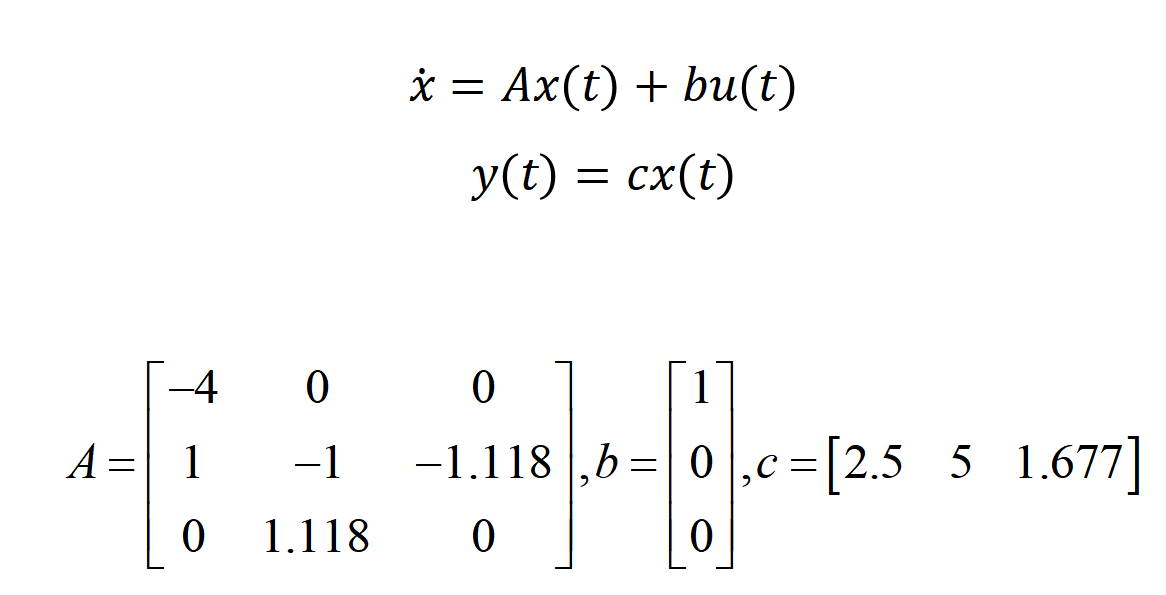
这里写出4阶龙格-库塔法在状态空间表达式下的显化实例，方便后续计算，5阶就不写了，太麻烦了。

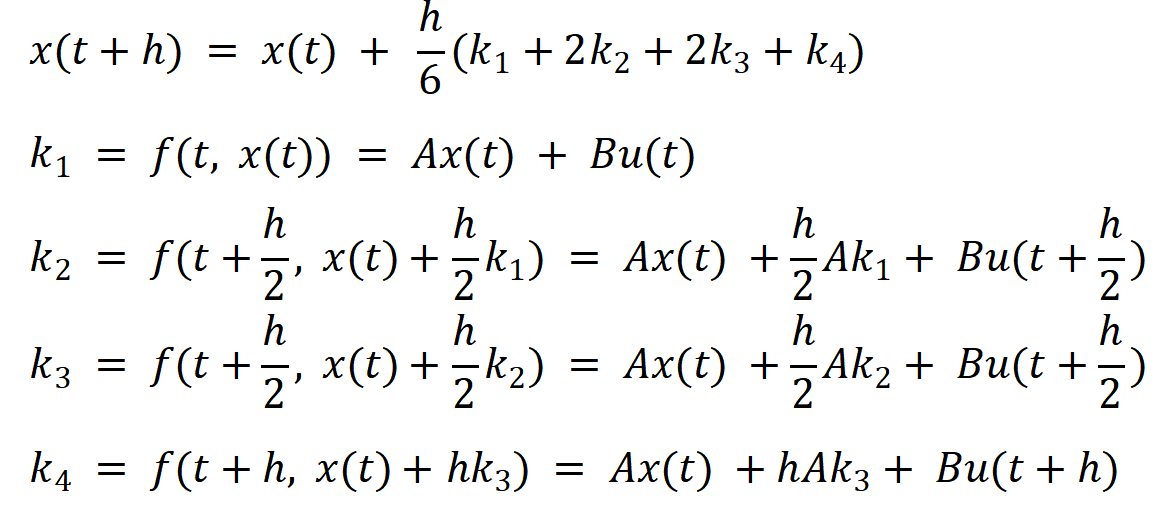
main.c

clear; close;h = 0.1; %h为步长
L = 30/h;%L为仿真长度
%表示出状态空间表达式各矩阵
A = [-4 0 0;1 -1 -1.118;0 1.118 0];
B = [1 0 0]';
C = [2.5 5 1.677];
%输入信号选为阶跃输入
u0 = 0;
ut = ones(1,L);
%n为系统阶次,x0表示系统状态初值
n = length(A);
x0 = zeros(n,1);
%因为是阶跃响应，除0外各时刻输入都是1，就都用u表示
u = u0;
xt_1 = x0;
xk_1 = x0;
xn_1 = x0;
%声明输出数据的空间大小
yt = zeros(1,L);
yk = zeros(1,L);
yn = zeros(1,L);
time = zeros(1,L);
for i = 1:Ltime(i) = i*h;%欧拉法 xt表示状态变量,yt(i)表示输出xt = xt_1 + h*(A*xt_1+B*u);yt(i) = C*xt;%4阶龙格-库塔法 xk表示状态变量,yk(i)表示输出%u(<h) = u = 0    u(>=h) = u(i) = 1k1 = A*xk_1+B*u;k2 = A*(xk_1+h*k1/2)+B*u;k3 = A*(xk_1+h*k2/2)+B*u;k4 = A*(xk_1+h*k3)+B*ut(i);xk = xk_1+h*(k1+2*k2+2*k3+k4)/6;yk(i) = C*xk;%5阶龙格-库塔法 xn表示状态变量,yn(i)表示输出%u(<h) = u = 0    u(>=h) = u(i) = 1k1 = A*xn_1+B*u;k2 = A*(xn_1+h*k1/4)+B*u;k3 = A*(xn_1+h*(3*k1/32 + 9*k2/32))+B*u;k4 = A*(xn_1+h*(1932*k1/2197 - 7200*k2/2197 + 7296*k3/2197))+B*u;k5 = A*(xn_1+h*(439*k1/216 - 8*k2 + 3680*k3/513 - 845*k4/4104))+B*ut(i);k6 = A*(xn_1+h*(-8*k1/27 + 2*k2 - 3544*k3/2565 + 1859*k4/4104 - 11*k5/40))+B*u;xn = xn_1 + h*(16*k1/135 + 6656*k3/12825 + 28561*k4/56430 - 9*k5/50 + 2*k6/55);yn(i) = C*xn;%数据更新xt_1 = xt;xk_1 = xk;xn_1 = xn;u = ut(i);
end
plot(time,ut,'k-.',time,yt,'b:',time,yk,'r--',time,yn,'g');
xlabel('t');
ylabel('yt、yk、yn');
legend('u(t)','Euler:yt','Runge-Kutta4:yk','Runge-Kutta5:yn');

如果看懂了上面讲解并且有部分matlab函数基础，这部分代码可以说是非常好理解，完全是按照公式的结构来写的。

plot(x, y1, 线型1, x, y2, 线型2, x, y3, 线型3)
用同一组 x 轴数据（time），绘制三组 (x,y) 曲线，每组曲线可独立设置线型、颜色。
'k-.'：黑色，-.（点划线）
'b:'：蓝色，虚线
'r--'：红色，--（双划线）
'g'：绿色，实线

四、结果分析

当h = 0.1时，可以看到三种方法最终都能稳定准确计算输出，欧拉法效果微差、4阶龙格-库塔法和5阶龙格-库塔法效果相同。

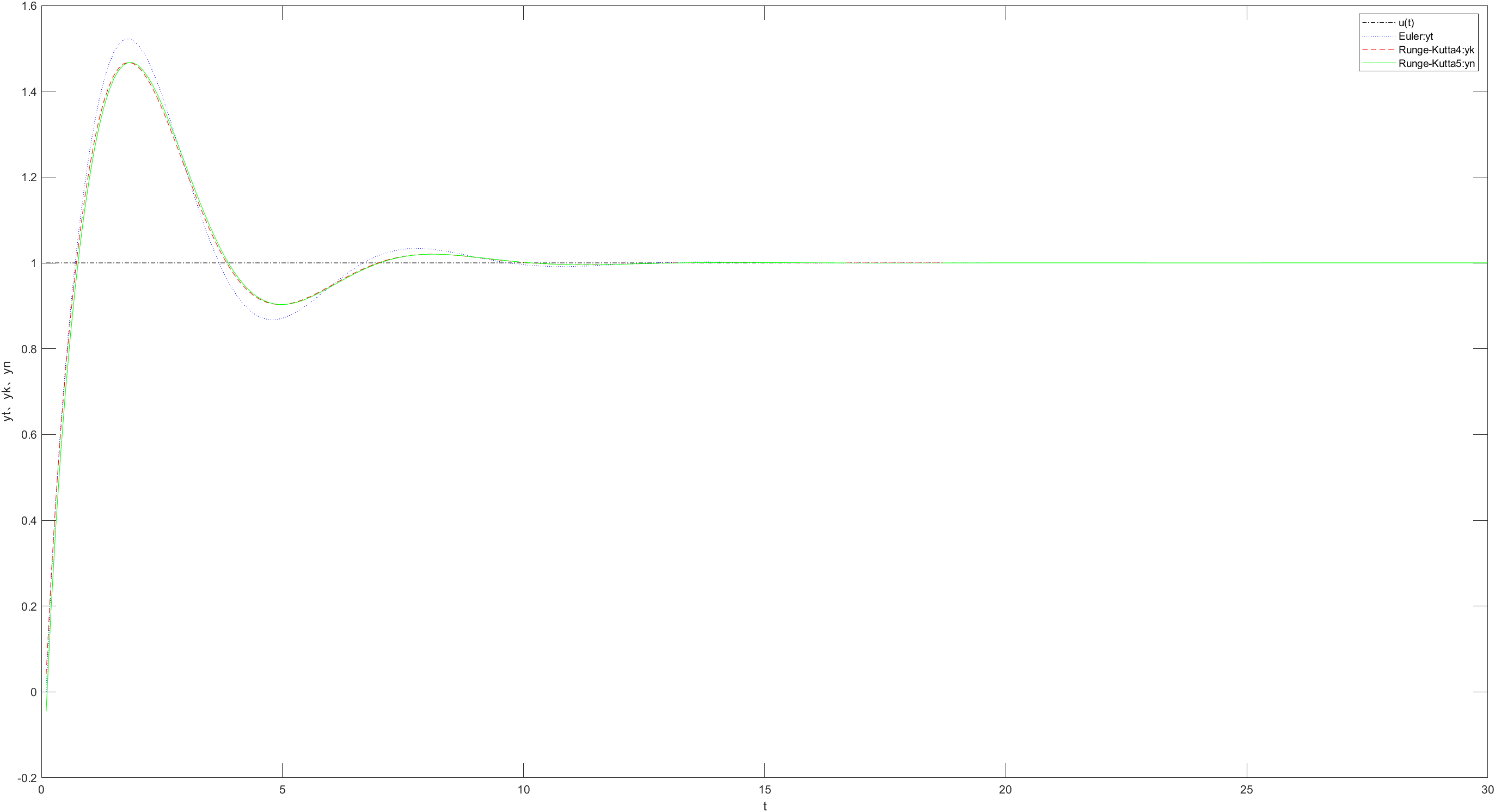
当h = 0.5时，欧拉法输出值震荡，4阶龙格-库塔法和5阶龙格-库塔法效果几乎相同。

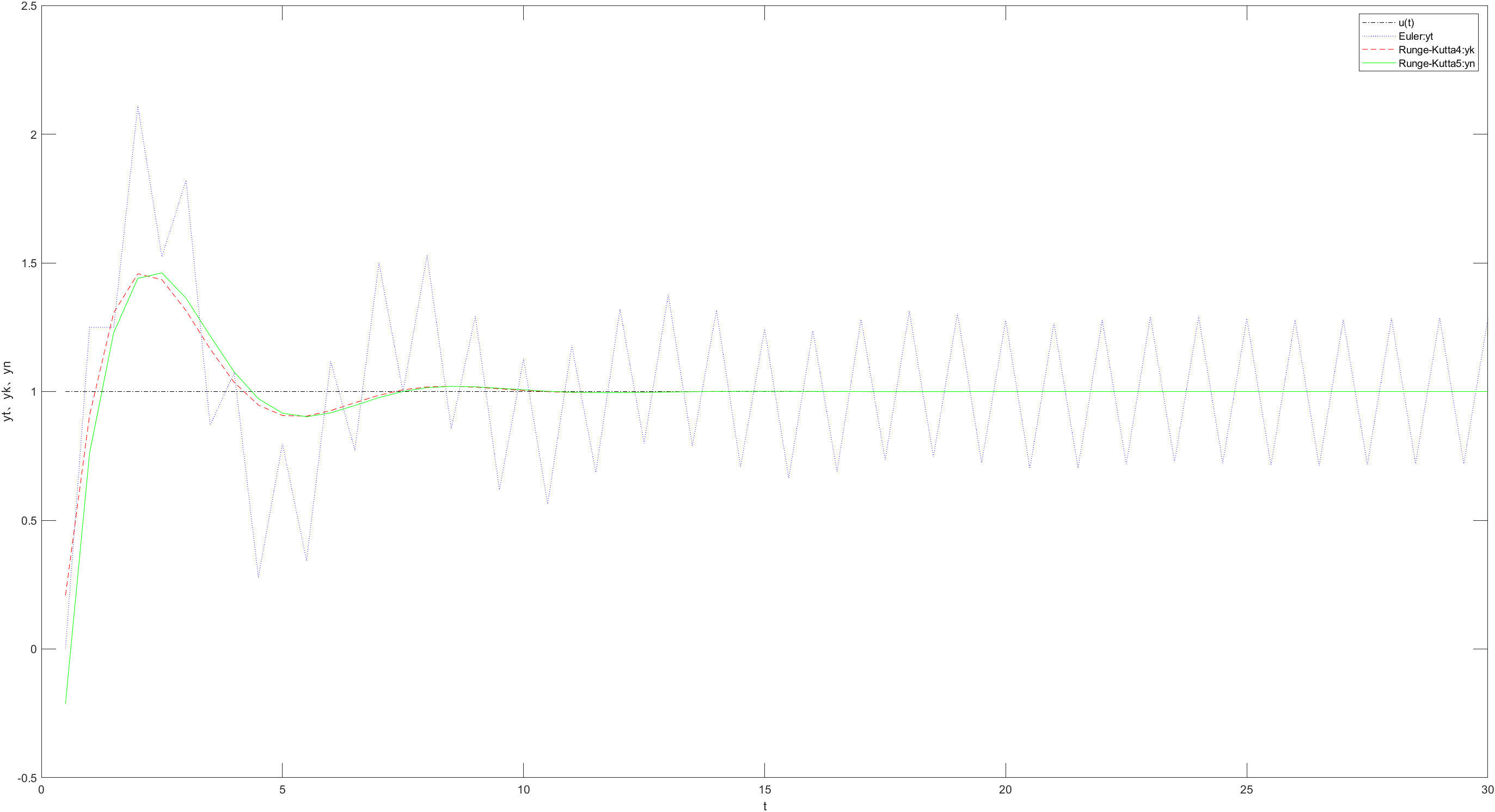
接下来在增大h值欧拉法输出值震荡发散，为了不影响效果，去除该值对比。
当h = 0.7时，4阶龙格-库塔法开始失效，5阶龙格-库塔法还能保持稳定。

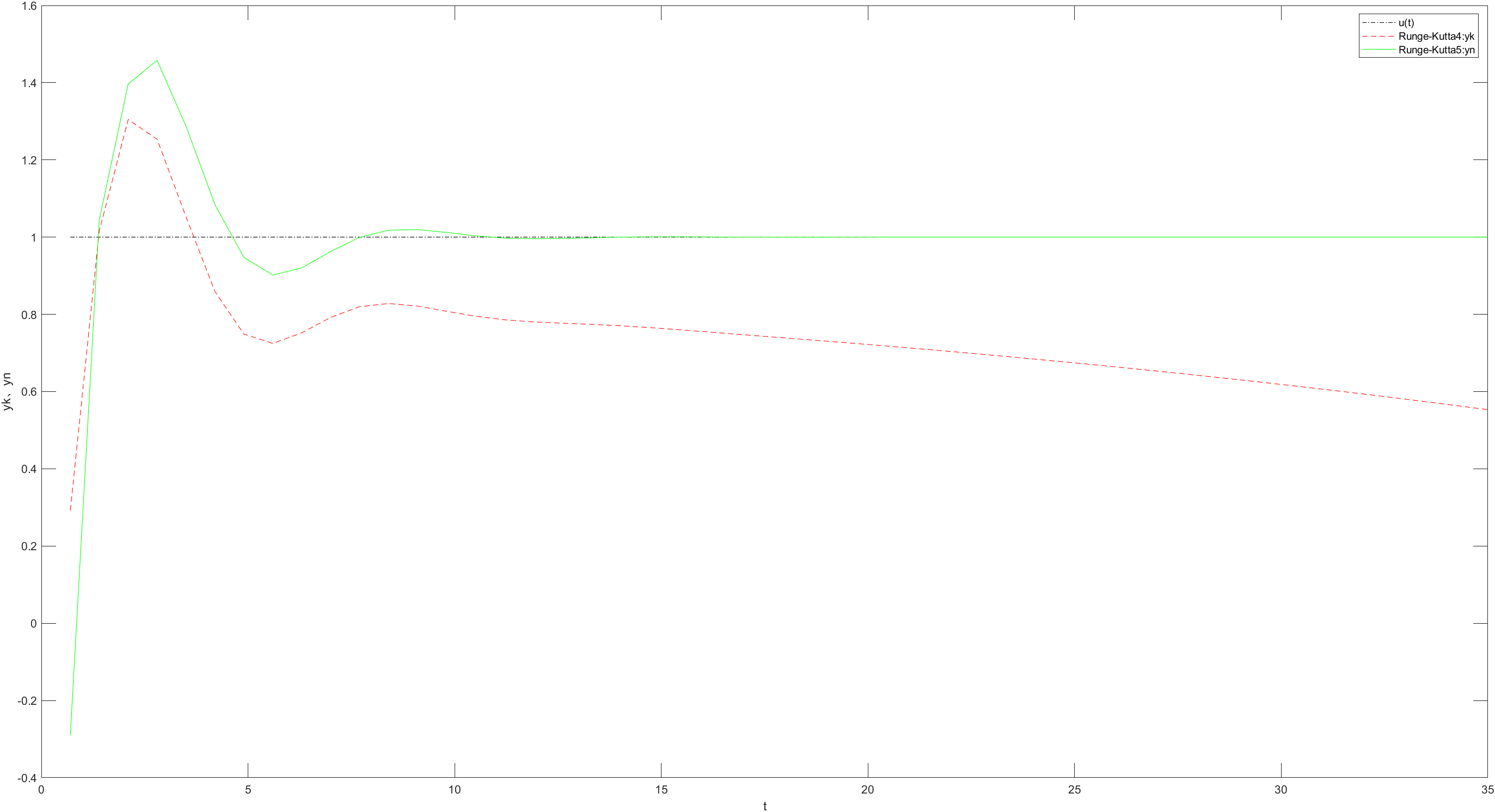
接下来在增大h值4阶龙格-库塔法输出值发散，为了不影响效果，去除该值对比。
当h = 0.9时，5阶龙格-库塔法渐近稳定，继续增大，将会发散失效。

---

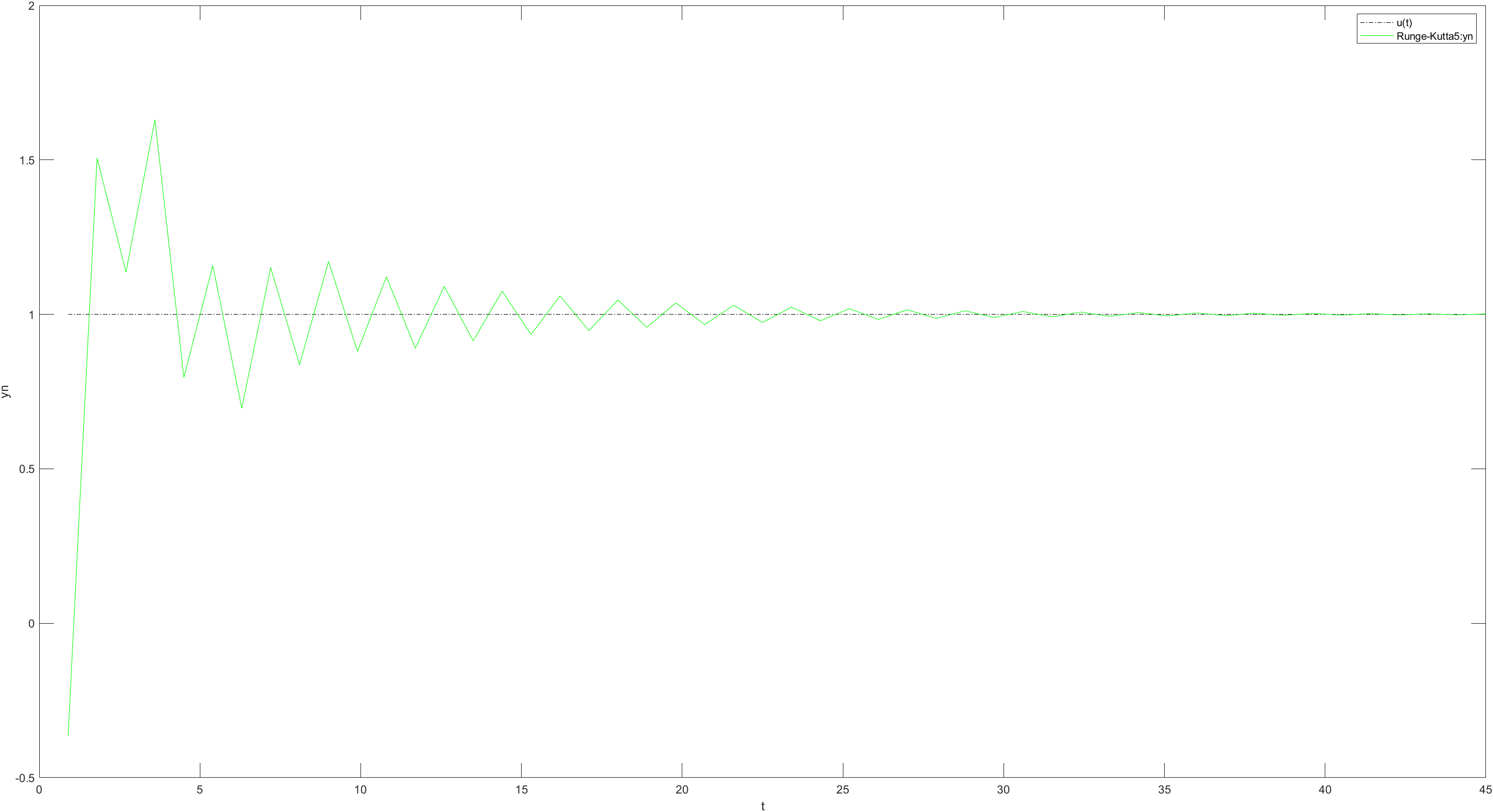
总结

可以看出，对于三阶系统而言
当实际中步长能达到0.1时，选欧拉法最合适，计算量小，效果同4阶龙格-库塔法和5阶龙格-库塔法几乎相同。
当步长能达到0.5时，选4阶龙格-库塔法。
当步长能达到0.7时，选5阶龙格-库塔法。
当步长达到0.9时，5阶龙格-库塔法也开始不稳了。