xtuoj 素数
题目
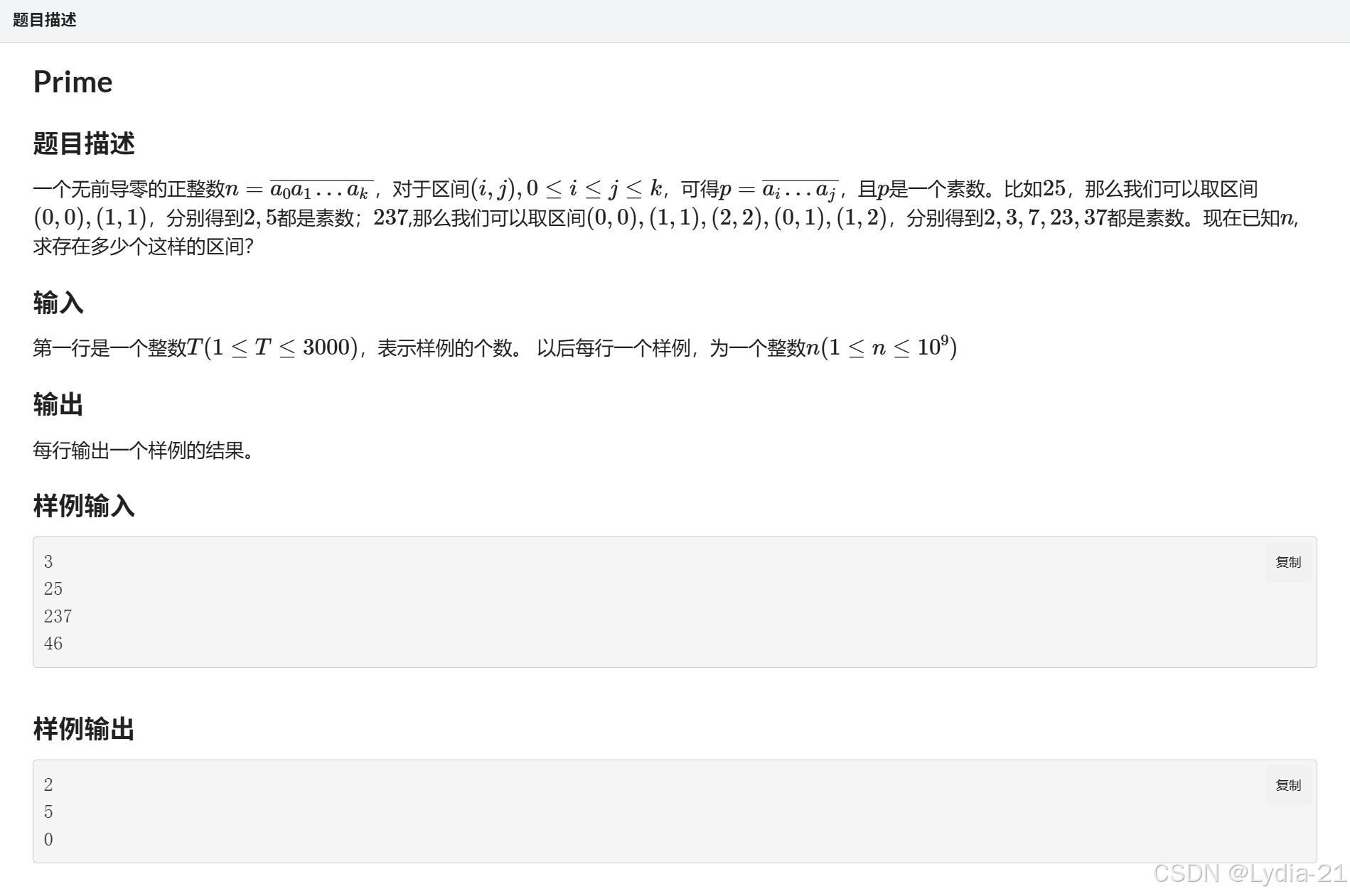
思路
关键点:如何得到所有的区间,如何判断是否为素数
首先解决如何得到所有的区间的问题。由前面进制转换的经验,我们可以知道,我们想要得到所有的区间,应该以字符串的形式读入,然后再将字符串转换为数字。如何将数字字符转换为数字,通过ascii码字符之间的关系知,只需 - '0' 即可。如何将字符串转为数字,只要把每个数字乘以他对应的权重再相加即可。常用的一个操作是num=num*base+digit,num首先初始化为0,然后从这里的digit依次从高位到低位取,最后得到的就是转换成数字以后的。要确定一个区间,肯定要先确定它的起点和终点,这里我们以 i 为起点,j 为终点,通过以下操作实现取得每个区间。下面的思路非常类似求最长子列和获取子列的思路。
for(int i=0;i<len;i++){ll num=0;for(int j=i;j<len;j++){num=num*10+(s[j]-'0');if(is_prime(num)) ans++;}}这段代码中用 s[j] - '0' 获取当前位的数字,配合配合内层循环中对 num 的更新逻辑,确实是一个非常巧妙的优化,核心在于利用已有计算结果避免重复运算,具体可以这样清晰描述:
-
s[j] - '0'的作用:字符串s中存储的是字符形式的数字(比如'1'、'2'),通过s[j] - '0'可以将字符转为对应的整数(比如'1' - '0' = 1),这是获取数字值的常规操作。 -
num的更新逻辑:复用已有结果,减少计算量:- 外层循环确定起点
i后,num仅初始化一次为0。 - 内层循环中,
j从i逐渐增加到len-1(即终点从起点开始不断后移):- 当
j = i时,num首次计算为s[i] - '0'(即起点位置的数字)。 - 当
j = i+1时,num无需重新从i到i+1计算,而是通过num = num * 10 + (s[j] - '0')得到:相当于将上一步的结果(i到i的数字)左移一位(乘以 10),再拼接上j=i+1位置的数字,直接得到i到i+1的完整数字。 - 后续
j继续增加时,重复上述逻辑:每次都基于上一个区间(i到j-1)的结果,左移一位后拼接新的数字s[j],即可得到当前区间(i到j)的数字。
- 当
- 外层循环确定起点
-
优势:这种方式避免了 “每次计算新区间时都从起点
i重新遍历到终点j” 的重复操作,而是通过 “累加拼接” 的方式复用之前的计算结果,将原本O(n²)的时间复杂度优化为实际执行中的线性操作(每个区间仅需一次简单运算),大大提升了效率。
例如,对于 s = "123",i=0 时:
j=0:num = 0 * 10 + 1 = 1(区间[0,0]);j=1:num = 1 * 10 + 2 = 12(区间[0,1],复用了j=0的结果1);j=2:num = 12 * 10 + 3 = 123(区间[0,2],复用了j=1的结果12)。
整个过程无需重复计算已处理过的位,逻辑简洁且高效。
再解决判断素数问题。这里直接使用试除法就好了,之前我本来打算用埃式筛法加预处理的,后来发现不行,这样的操作使用于那种n<10^6这种且需要进行大量判断素数的情况,也就是说n差不多10^6,然后T也比较大的时候。这里的n是10^9,而且埃式筛法和欧拉筛法都需要额外用一个数组存素数,比较时候打表,判断一片区间的情况。
这里我加了一个小小的优化,但其实没啥区别,就是把偶数的全都排除,记得要把2设为素数。
bool is_prime(int n){if(n<2) return false;if(n==2) return true;if(n%2==0) return false;for(int i=3;i<=n/i;i+=2)if(n%i==0) return false;return true;
}还可以在把3的倍数也去掉
bool is_prime(long long n) {if (n < 2) return false;if (n == 2) return true;if (n % 2 == 0) return false;if (n == 3) return true;if (n % 3 == 0) return false;long long limit = sqrt(n) + 1;for (long long i = 5; i <= limit; i += 6) {if (n % i == 0 || n % (i + 2) == 0) {return false;}}return true;
}当然普通的试除法就够了
bool is_prime(int n){if(n<2) return false;if(n==2) return true;for(int i=2;i<=n/i;i++){if(n%i==0) return false;}return true;
}代码
#include<stdio.h>
#include<string.h>
#include<stdbool.h>
#define ll long longint T,ans;
char s[10];bool is_prime(int n){if(n<2) return false;if(n==2) return true;if(n%2==0) return false;for(int i=3;i<=n/i;i+=2)if(n%i==0) return false;return true;
}void game(){scanf("%s",s);int len=strlen(s);ans=0;for(int i=0;i<len;i++){ll num=0;for(int j=i;j<len;j++){num=num*10+(s[j]-'0');if(is_prime(num)) ans++;}}printf("%d\n",ans);
}int main(){scanf("%d",&T);while(T--){game();}return 0;
}