插值——拉格朗日插值
插值——拉格朗日插值
- 插值任务简介
- 插值目标函数
- 拉格朗日插值原理(详细推导)
- 1. 问题的唯一性与存在性
- 2. 拉格朗日基函数的构造思想
- 3. 拉格朗日基函数的显式表达式
- 4. 拉格朗日插值多项式
- 5. 插值余项(误差分析)
- 6. 拉格朗日插值的优缺点
- 7. 改进方向:切比雪夫节点
- Python 实现
- 结果展示
- 附:文章说明
插值任务简介
在科学计算、工程建模与数据处理中,我们常常面对如下问题:
已知某个未知函数 f(x)f(x)f(x) 在若干离散点 {xi}i=0n\{x_i\}_{i=0}^n{xi}i=0n 处的函数值 {yi=f(xi)}i=0n\{y_i = f(x_i)\}_{i=0}^n{yi=f(xi)}i=0n,希望构造一个“简单”的函数 P(x)P(x)P(x),使得
P(xi)=yi,i=0,1,…,nP(x_i) = y_i, \quad i = 0, 1, \dots, n P(xi)=yi,i=0,1,…,n
并用 P(x)P(x)P(x) 来近似 f(x)f(x)f(x) 在其他点的取值。
这一过程称为 插值(Interpolation),函数 P(x)P(x)P(x) 称为 插值函数。
在众多插值方法中,拉格朗日插值是一种经典的全局多项式插值方法,它构造一个次数不超过 nnn 的多项式,精确通过所有 n+1n+1n+1 个给定数据点。本文将深入剖析其数学原理、构造过程与内在特性。
插值目标函数
为便于演示,设定真实函数为:
f(x)=sinx+cosx,x∈[a,b]f(x) = \sin x + \cos x, \quad x \in [a, b] f(x)=sinx+cosx,x∈[a,b]
在区间 [a,b][a, b][a,b] 上取 n+1n+1n+1 个互异节点 x0,x1,…,xnx_0, x_1, \dots, x_nx0,x1,…,xn(通常等距),对应函数值为 yi=f(xi)y_i = f(x_i)yi=f(xi)。
目标:构造多项式 Pn(x)P_n(x)Pn(x) 满足插值条件:
Pn(xi)=yi,i=0,1,…,nP_n(x_i) = y_i, \quad i = 0, 1, \dots, n Pn(xi)=yi,i=0,1,…,n
拉格朗日插值原理(详细推导)
1. 问题的唯一性与存在性
定理(插值多项式存在唯一性):
给定 n+1n+1n+1 个互异节点 x0,x1,…,xnx_0, x_1, \dots, x_nx0,x1,…,xn 及对应的函数值 y0,y1,…,yny_0, y_1, \dots, y_ny0,y1,…,yn,存在唯一的次数不超过 nnn 的多项式 Pn(x)P_n(x)Pn(x) 满足:
Pn(xi)=yi,∀i=0,1,…,nP_n(x_i) = y_i, \quad \forall i = 0, 1, \dots, n Pn(xi)=yi,∀i=0,1,…,n
证明思路:
设 Pn(x)=a0+a1x+⋯+anxnP_n(x) = a_0 + a_1 x + \cdots + a_n x^nPn(x)=a0+a1x+⋯+anxn,代入插值条件得线性方程组:
[1x0x02⋯x0n1x1x12⋯x1n⋮⋮⋮⋱⋮1xnxn2⋯xnn][a0a1⋮an]=[y0y1⋮yn]\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^n \\ 1 & x_1 & x_1^2 & \cdots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^n \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix}= \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \end{bmatrix} 11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0nx1n⋮xnna0a1⋮an=y0y1⋮yn
该系数矩阵为 范德蒙德矩阵(Vandermonde Matrix),其行列式为:
det(V)=∏0≤i<j≤n(xj−xi)\det(V) = \prod_{0 \le i < j \le n} (x_j - x_i) det(V)=0≤i<j≤n∏(xj−xi)
由于所有 xix_ixi 互异,det(V)≠0\det(V) \ne 0det(V)=0,故方程组有唯一解。
因此,满足插值条件的 nnn 次多项式存在且唯一。
2. 拉格朗日基函数的构造思想
直接求解上述线性方程组计算量大。
拉格朗日方法:不直接求系数 aka_kak,而是构造一组特殊的基函数 {ℓk(x)}k=0n\{\ell_k(x)\}_{k=0}^n{ℓk(x)}k=0n,使得:
- 每个 ℓk(x)\ell_k(x)ℓk(x) 是一个 nnn 次多项式;
- ℓk(xi)={1,i=k0,i≠k\ell_k(x_i) = \begin{cases} 1, & i = k \\ 0, & i \ne k \end{cases}ℓk(xi)={1,0,i=ki=k(即“选择性”)
若能构造出这样的基函数,则插值多项式可直接写为:
Pn(x)=y0ℓ0(x)+y1ℓ1(x)+⋯+ynℓn(x)=∑k=0nykℓk(x)P_n(x) = y_0 \ell_0(x) + y_1 \ell_1(x) + \cdots + y_n \ell_n(x) = \sum_{k=0}^n y_k \ell_k(x) Pn(x)=y0ℓ0(x)+y1ℓ1(x)+⋯+ynℓn(x)=k=0∑nykℓk(x)
因为当 x=xix = x_ix=xi 时,只有 ℓi(xi)=1\ell_i(x_i) = 1ℓi(xi)=1,其余为 0,故 Pn(xi)=yiP_n(x_i) = y_iPn(xi)=yi,完美满足插值条件。
3. 拉格朗日基函数的显式表达式
要构造满足 ℓk(xi)=δik\ell_k(x_i) = \delta_{ik}ℓk(xi)=δik 的 nnn 次多项式,考虑:
- ℓk(x)\ell_k(x)ℓk(x) 必须在所有 xjx_jxj(j≠kj \ne kj=k)处为零 → 所以它必须包含因子 (x−xj)(x - x_j)(x−xj) 对所有 j≠kj \ne kj=k;
- 因此,ℓk(x)\ell_k(x)ℓk(x) 的分子应为:
∏j=0j≠kn(x−xj)\prod_{\substack{j=0 \\ j \ne k}}^n (x - x_j) j=0j=k∏n(x−xj)
这是一个 nnn 次多项式,在 x=xjx = x_jx=xj(j≠kj \ne kj=k)处为零; - 但此时 ℓk(xk)=∏j≠k(xk−xj)≠1\ell_k(x_k) = \prod_{j \ne k} (x_k - x_j) \ne 1ℓk(xk)=∏j=k(xk−xj)=1,需归一化;
- 除以该值,即可使 ℓk(xk)=1\ell_k(x_k) = 1ℓk(xk)=1。
于是得到拉格朗日基函数的定义:
ℓk(x)=∏j=0j≠knx−xjxk−xjfor k=0,1,…,n\ell_k(x) = \prod_{\substack{j=0 \\ j \ne k}}^{n} \frac{x - x_j}{x_k - x_j} \quad \text{for } k = 0, 1, \dots, n ℓk(x)=j=0j=k∏nxk−xjx−xjfor k=0,1,…,n
性质总结:
- deg(ℓk)=n\deg(\ell_k) = ndeg(ℓk)=n
- ℓk(xi)=δik\ell_k(x_i) = \delta_{ik}ℓk(xi)=δik
- ∑k=0nℓk(x)≡1\sum_{k=0}^n \ell_k(x) \equiv 1∑k=0nℓk(x)≡1(因为若所有 yk=1y_k = 1yk=1,则插值多项式恒为 1)
4. 拉格朗日插值多项式
将基函数线性组合,得到最终的插值多项式:
Pn(x)=∑k=0nykℓk(x)=∑k=0nyk(∏j=0j≠knx−xjxk−xj)P_n(x) = \sum_{k=0}^{n} y_k \, \ell_k(x) = \sum_{k=0}^{n} y_k \left( \prod_{\substack{j=0 \\ j \ne k}}^{n} \frac{x - x_j}{x_k - x_j} \right) Pn(x)=k=0∑nykℓk(x)=k=0∑nykj=0j=k∏nxk−xjx−xj
此式即为 拉格朗日插值公式。它是对插值问题的一个显式解,无需解线性方程组。
5. 插值余项(误差分析)
虽然 Pn(xi)=yiP_n(x_i) = y_iPn(xi)=yi,但在非节点处存在误差。若 f(x)f(x)f(x) 在包含所有节点的区间上具有 n+1n+1n+1 阶连续导数,则对任意 x∈[a,b]x \in [a, b]x∈[a,b],存在 ξ\xiξ 介于 xxx 与节点之间,使得:
f(x)−Pn(x)=f(n+1)(ξ)(n+1)!⋅ωn+1(x)f(x) - P_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \cdot \omega_{n+1}(x) f(x)−Pn(x)=(n+1)!f(n+1)(ξ)⋅ωn+1(x)
其中
ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)\omega_{n+1}(x) = (x - x_0)(x - x_1)\cdots(x - x_n) ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)
关键结论:
- 误差与 f(n+1)(ξ)f^{(n+1)}(\xi)f(n+1)(ξ) 和节点多项式 ωn+1(x)\omega_{n+1}(x)ωn+1(x) 有关;
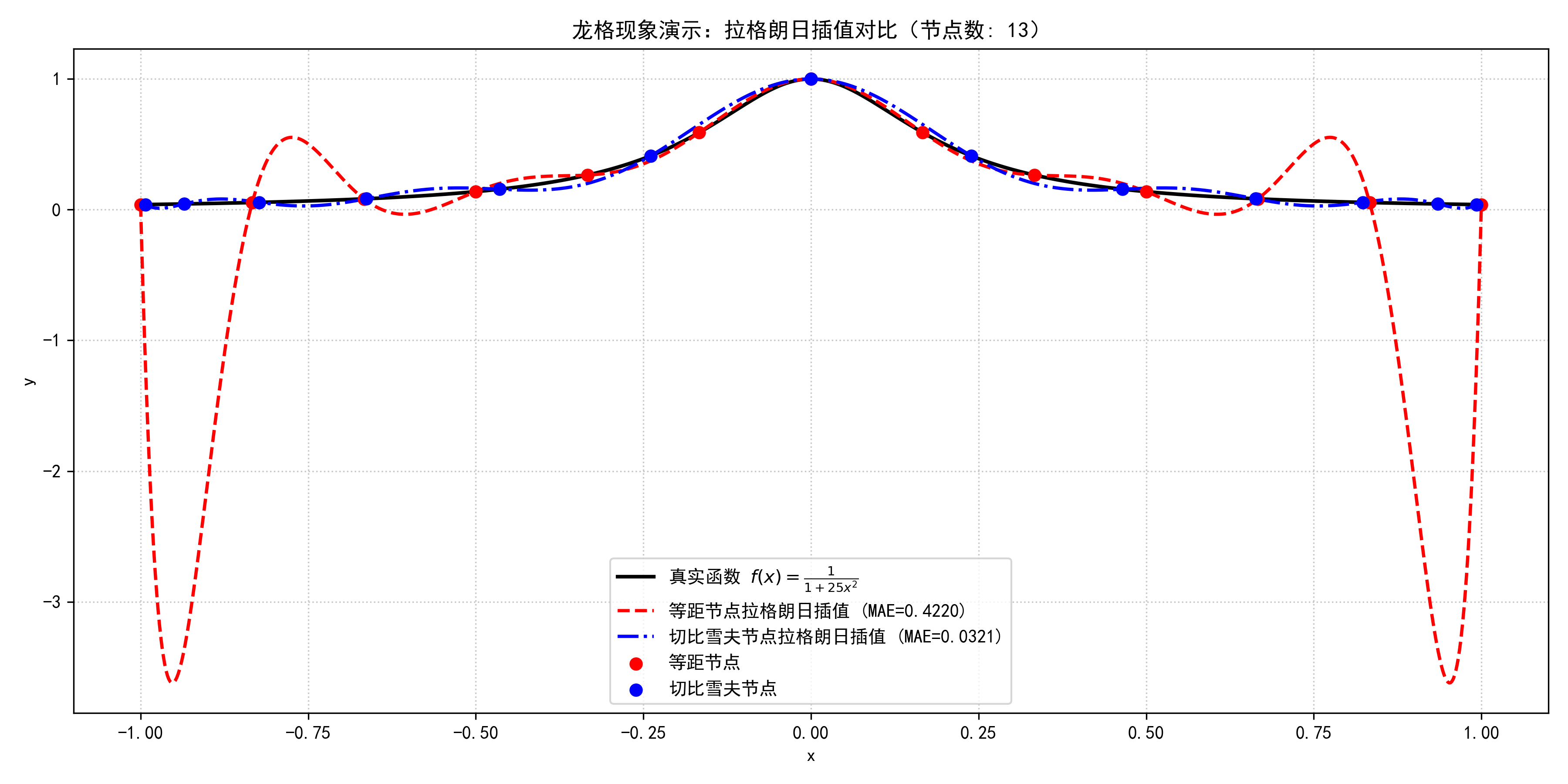
- 当 nnn 增大时,(n+1)!(n+1)!(n+1)! 增长快,ωn+1(x)\omega_{n+1}(x)ωn+1(x) 在端点附近可能极大(尤其等距节点)。这便是龙格现象:高次插值在边界误差爆炸。
6. 拉格朗日插值的优缺点
| 优点 | 缺点 |
|---|---|
| 显式表达式,无需解方程组 | 全局性:任一节点变动,所有 ℓk(x)\ell_k(x)ℓk(x) 需重算 |
| 数学形式简洁优美 | 计算复杂度高:求值需 O(n2)O(n^2)O(n2) 次运算 |
| 理论价值高,便于误差分析 | 数值不稳定:高次时舍入误差放大 |
| 适用于小规模精确插值 | 龙格现象:等距高次插值在端点振荡 |
7. 改进方向:切比雪夫节点
为抑制龙格现象,可将插值节点从等距分布改为切比雪夫节点(Chebyshev Nodes):
xk=a+b2+b−a2cos((2k+1)π2(n+1)),k=0,1,…,nx_k = \frac{a + b}{2} + \frac{b - a}{2} \cos\left( \frac{(2k + 1)\pi}{2(n + 1)} \right), \quad k = 0, 1, \dots, n xk=2a+b+2b−acos(2(n+1)(2k+1)π),k=0,1,…,n
这些节点在区间两端更密集,能最小化 max∣ωn+1(x)∣\max |\omega_{n+1}(x)|max∣ωn+1(x)∣,从而显著提升插值稳定性。
例如,对函数
f(x)=11+25x2f(x) = \frac{1}{1 + 25x^2} f(x)=1+25x21
在区间 [−1,1][-1, 1][−1,1] 上使用等距节点进行拉格朗日插值,当插值次数 n→∞n \to \inftyn→∞ 时,插值多项式 Pn(x)P_n(x)Pn(x) 在区间端点附近会出现发散现象,而不会一致收敛到 f(x)f(x)f(x)。
Python 实现
以下代码支持拉格朗日插值,并可对比等距节点与切比雪夫节点的效果。
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
matplotlib.rcParams['axes.unicode_minus'] = False # 正常显示负号# ========== 配置参数 ==========
INTERVAL = (-5.0, 5.0) # 插值区间 [a, b]
N = 12 # 插值点数 = N + 1
C, D, E, F = 1.0, 1.0, 1.0, 1.0 # 目标函数参数
M = 1000 # 测试点数量(用于误差和绘图)
RESULT_DIR = 输出目录# ========== 目标函数 ==========
def target_function(x):"""f(x) = c*sin(d*x) + e*cos(f*x)"""return C * np.sin(D * x) + E * np.cos(F * x)# ========== 拉格朗日插值函数 ==========
def lagrange_interp(x_nodes, y_nodes, x_query):"""在 x_nodes, y_nodes 上对 x_query 进行拉格朗日插值"""x_nodes = np.asarray(x_nodes)y_nodes = np.asarray(y_nodes)x_query = np.asarray(x_query)n = len(x_nodes)result = np.zeros_like(x_query, dtype=np.float64)for k in range(n):# 计算 ℓ_k(x)Lk = np.ones_like(x_query, dtype=np.float64)denom = 1.0for j in range(n):if j != k:Lk *= (x_query - x_nodes[j])denom *= (x_nodes[k] - x_nodes[j])result += y_nodes[k] * (Lk / denom)return result# ========== 切比雪夫节点生成函数 ==========
def chebyshev_nodes(a, b, n):"""生成 n+1 个切比雪夫节点"""k = np.arange(0, n + 1)return (a + b) / 2 + (b - a) / 2 * np.cos((2 * k + 1) * np.pi / (2 * (n + 1)))# ========== 主程序 ==========
def main():os.makedirs(RESULT_DIR, exist_ok=True)a, b = INTERVAL# 1. 构造插值节点(等距)x_eq = np.linspace(a, b, N + 1)y_eq = target_function(x_eq)# 2. 构造插值节点(切比雪夫)x_cheb = chebyshev_nodes(a, b, N)y_cheb = target_function(x_cheb)# 3. 生成测试点(用于绘图和误差)x_test = np.linspace(a, b, M)y_true = target_function(x_test)y_eq_interp = lagrange_interp(x_eq, y_eq, x_test)y_cheb_interp = lagrange_interp(x_cheb, y_cheb, x_test)# 4. 计算平均绝对误差mae_eq = np.mean(np.abs(y_eq_interp - y_true))mae_cheb = np.mean(np.abs(y_cheb_interp - y_true))print(f"等距节点拉格朗日插值的平均绝对误差 (MAE): {mae_eq:.6f}")print(f"切比雪夫节点拉格朗日插值的平均绝对误差 (MAE): {mae_cheb:.6f}")# 5. 绘图plt.figure(figsize=(12, 6))plt.plot(x_test, y_true, 'k-', linewidth=1.8, label=r'真实函数 $f(x) = \sin x + \cos x$')plt.plot(x_test, y_eq_interp, 'r--', linewidth=1.5, label=f'等距节点拉格朗日插值 (MAE={mae_eq:.4f})')plt.plot(x_test, y_cheb_interp, 'b-.', linewidth=1.5, label=f'切比雪夫节点拉格朗日插值 (MAE={mae_cheb:.4f})')plt.scatter(x_eq, y_eq, color='red', s=30, zorder=5, label='等距节点')plt.scatter(x_cheb, y_cheb, color='blue', s=30, zorder=5, label='切比雪夫节点')plt.grid(True, linestyle=':', alpha=0.7)plt.legend()plt.title(f'拉格朗日插值对比(节点数: {N+1})')plt.xlabel('x')plt.ylabel('y')plt.tight_layout()plot_path = os.path.join(RESULT_DIR, 'lagrange_comparison.png')plt.savefig(plot_path, dpi=300)print(f"结果图已保存至: {plot_path}")plt.show()if __name__ == '__main__':main()
结果展示
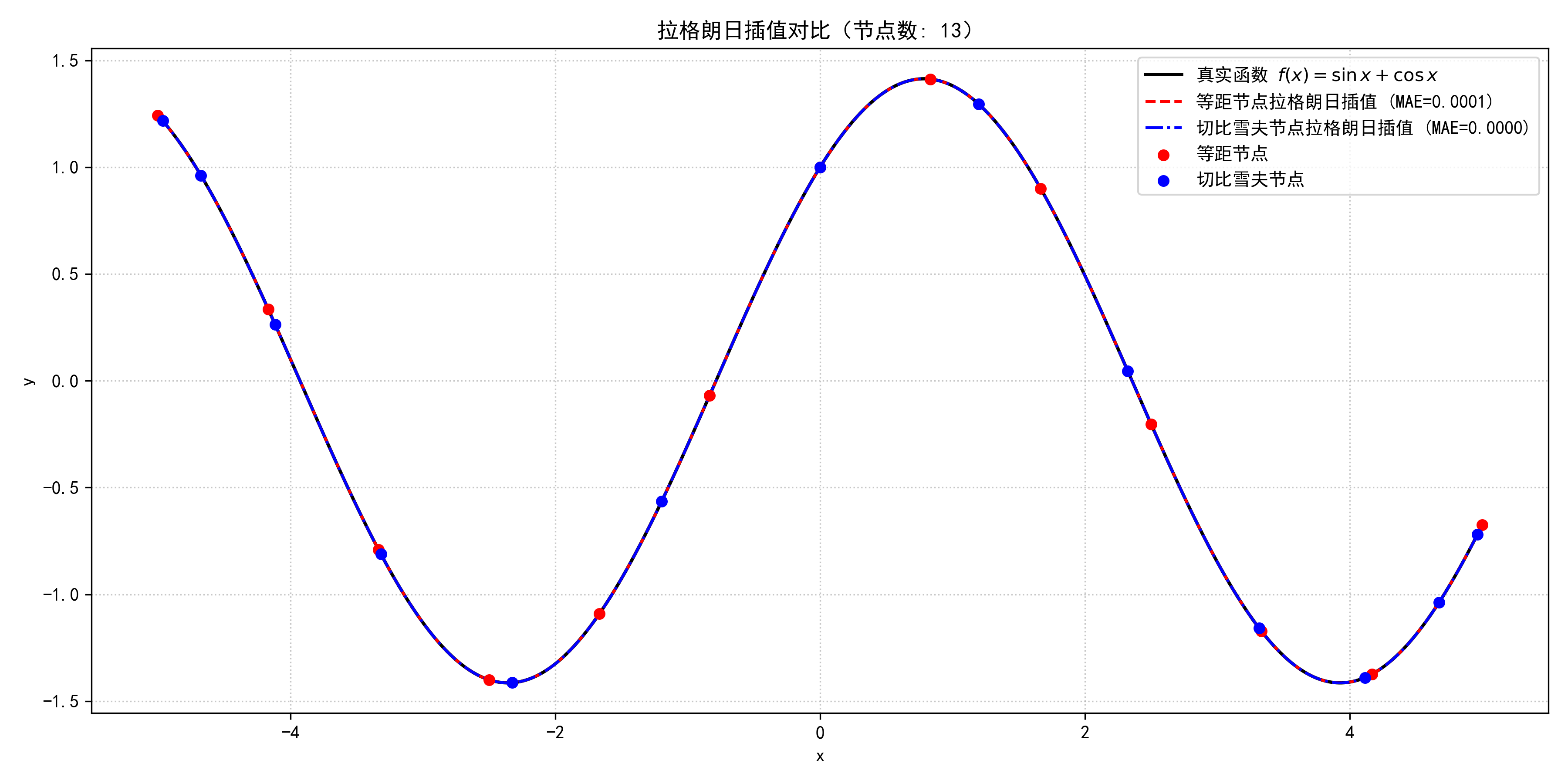
等距节点拉格朗日插值的平均绝对误差 (MAE): 0.000057
切比雪夫节点拉格朗日插值的平均绝对误差 (MAE): 0.000020
附:文章说明
本文仅为个人理解,若有不当之处,欢迎指正~
