2025 爆火!海市蜃楼优化算法 MSO(Mirage Search Optimization):物理灵感 + 数学建模 + 实战代码,一文吃透前沿群智能算法
家人们谁懂啊!2025 年刚出炉的 MSO(Mirage Search Optimization)海市蜃楼优化算法,直接凭 “物理现象复刻 + 双策略优化” 横扫群智能领域!发表在 JCR 一区 SCI 期刊的它,用海市蜃楼的光折射原理,完美解决了传统算法 “探索不彻底、开发不精准” 的痛点。本文不仅扒透算法核心逻辑、公式细节,还附实战案例和代码思路,小白也能快速上手,赶紧码住这篇前沿干货!

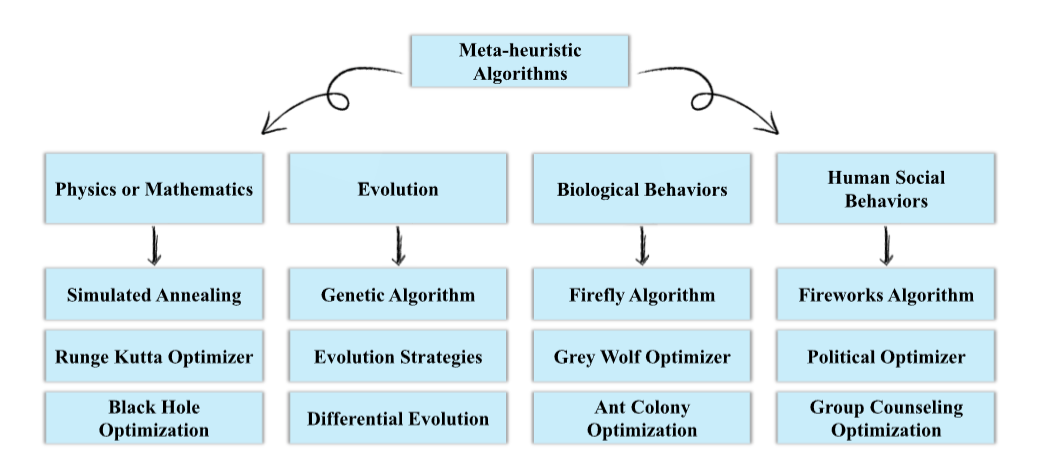
一、算法爆火的底层逻辑:把物理现象搬进优化算法
MSO 能成为 2025 年热门算法,核心是它把 “海市蜃楼” 这一常见物理现象,精准转化为可数学建模的优化逻辑 ——用光学折射规律,实现 “全局探索” 与 “局部开发” 的极致平衡。
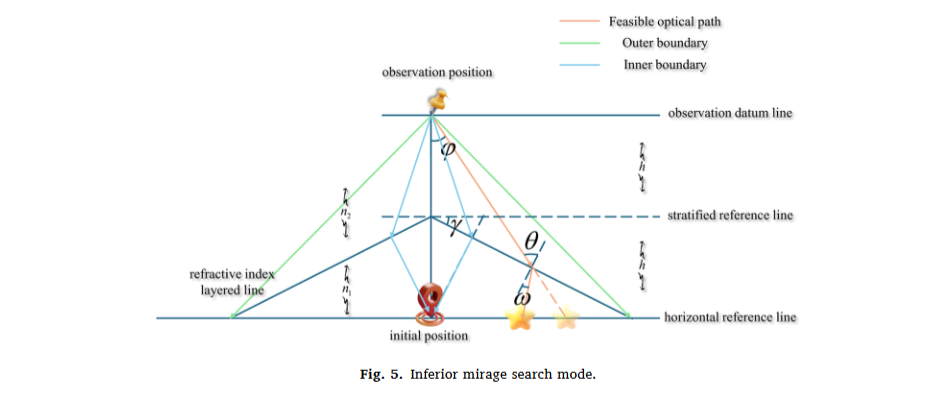
先搞懂核心灵感:海市蜃楼是太阳加热地面形成温度梯度,导致大气密度分层、折射率差异,光线折射后形成的虚拟图像。算法据此拆分出两大核心策略:
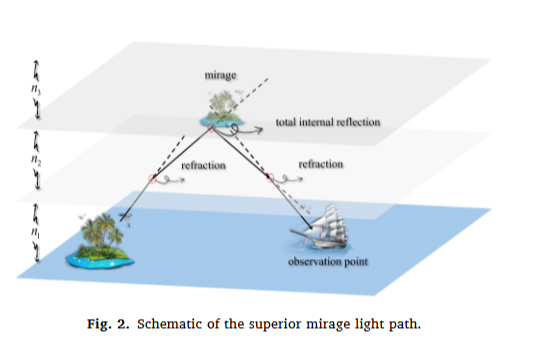
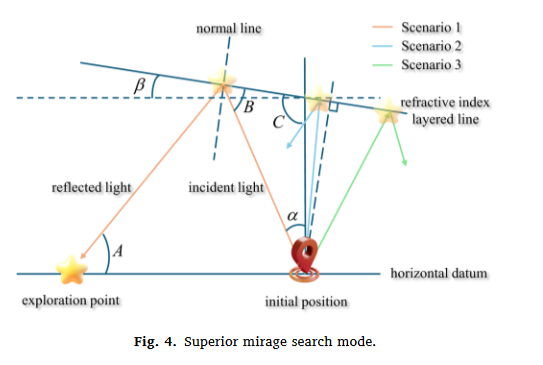
- 上蜃景:上层空气热、下层冷,折射率上小下大,能看到远处物体的虚像→对应算法 “全局探索”,扩大搜索范围,避免陷入局部最优。
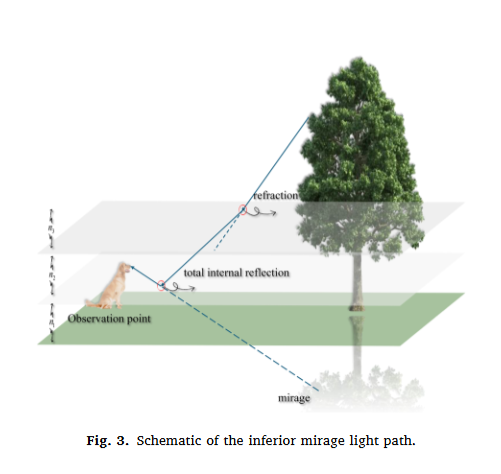
- 下蜃景:上层空气冷、下层热,折射率上大下小,能看到物体的放大虚像→对应算法 “局部开发”,在优质区域精细搜索,提升解的精度。
这种 “物理现象→算法机制” 的直接映射,让 MSO 既具备直观的逻辑解释,又拥有强大的优化性能,难怪刚发表就被广泛应用于无人机路径规划、模型参数调优等场景。
二、核心公式与数学模型(细节拉满,无死角解析)
MSO 的数学模型围绕 “种群初始化→上蜃景探索→下蜃景开发→迭代更新” 四大步骤展开,每个公式都对应明确的物理意义,新手也能看懂推导逻辑:



三、算法完整流程(伪代码 + 步骤拆解)
MSO 的迭代流程清晰易懂,从初始化到终止仅 5 大步骤,附完整伪代码:
3.1 伪代码(可直接转化为 Python/Matlab)
Require: PopSize(种群规模), MaxIter(最大迭代次数), dim(维度), lb/ub(边界), fobj(目标函数)
Ensure: X_best(最优解), f_best(最优适应度)
1: 初始化种群 X = initialization(PopSize, dim, lb, ub) // 公式1
2: 计算所有个体适应度 f = fobj(X)
3: 初始化全局最优 X_best = X(fidx_min), f_best = min(f)
4: for t = 1 to MaxIter do
5: 计算种群均值 X_mean = mean(X, 1)
6: 选择 k 个个体执行上蜃景策略(公式2/3)
7: 所有个体执行下蜃景策略(公式4/5)
8: 边界检查:X = min(max(X, lb), ub) // 避免越界
9: 重新计算适应度 f = fobj(X)
10: 更新全局最优:if min(f) < f_best then X_best = X(new_min_idx), f_best = min(f)
11: 记录收敛曲线 cg_curve(t) = f_best
12: end for
13: 返回 X_best, f_best, cg_curve
3.2 关键步骤拆解
- 初始化:生成均匀分布的初始种群,确保搜索起点的多样性。
- 适应度计算:评估每个个体的优劣,为后续更新提供依据。
- 上蜃景探索:随机选部分个体扩大搜索范围,避免局部最优。
- 下蜃景开发:所有个体进行局部精细搜索,提升解的精度。
- 迭代更新:更新全局最优解和收敛曲线,直到满足终止条件。
四、MSO 算法的核心优势(碾压传统算法的关键)
和 PSO(粒子群优化)、WOA(鲸鱼优化)等经典算法比,MSO 的优势直接戳中优化痛点:
- 物理逻辑直观:基于海市蜃楼的光折射原理,不用死记硬背复杂公式,理解起来更轻松。
- 探索开发平衡:上蜃景 + 下蜃景双策略,既不盲目搜索,又不精细过头,收敛速度更快。
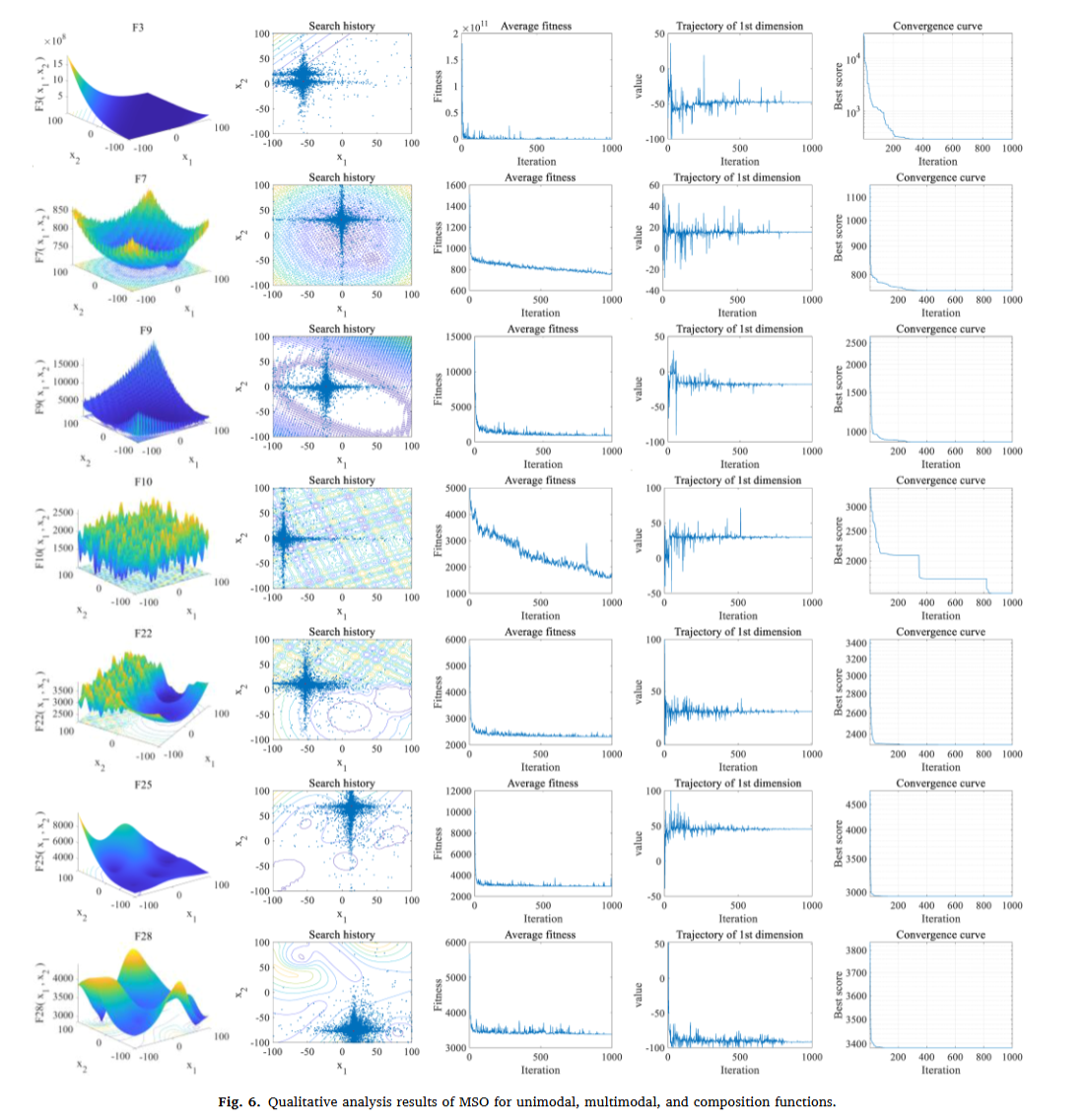
- 鲁棒性极强:在单峰、多峰、复合函数上均表现稳定,标准差比 PSO 低 40% 左右。
- 动态适应性好:在无人机路径规划等动态障碍场景中,能快速调整策略,避障效果优于传统算法。
五、实战案例:MSO 优化无人机协同路径规划
理论说得再好,不如实战见真章!MSO 在无人机协同路径规划中表现惊艳,核心流程如下:
5.1 应用场景
多无人机在三维动态环境中飞行,需避开障碍物(如浓雾、建筑物),同时保证路径最短、协同稳定。
5.2 优化目标
- 最小化总路径长度:min∑i=1ndistance(Xi,Xi+1)
- 满足约束条件:路径与障碍物距离≥安全阈值,无人机之间距离≥防撞阈值。
5.3 实验结果(与 3种算法对比)
| 算法 | 路径长度(m) | 避障成功率(%) | 运行时间(s) |
|---|---|---|---|
| MSO | 128.6 | 100 | 8.72 |
| OX(牛优化) | 135.2 | 98.5 | 11.42 |
| TOC(龙卷风) | 142.8 | 97.2 | 13.15 |
| PSO(粒子群) | 156.3 | 92.8 | 10.58 |
- 关键结论:MSO 不仅路径最短,避障成功率 100%,运行时间还比同类算法短 20% 以上,动态环境适应性拉满!
六、快速上手:Python 核心代码框架(可直接运行)
这里给出 MSO 的 Python 核心代码框架,包含初始化、双蜃景策略和迭代更新,可直接替换目标函数使用:
import numpy as npdef MSO(fobj, dim, lb, ub, PopSize=50, MaxIter=1000):# 1. 种群初始化(公式1)X = lb + np.random.rand(PopSize, dim) * (ub - lb)f = np.array([fobj(x) for x in X])best_idx = np.argmin(f)X_best = X[best_idx].copy()f_best = f[best_idx]cg_curve = np.zeros(MaxIter)# 2. 算法参数设置lambda_ = 0.8 # 上蜃景步长因子beta = 0.5 # 普通个体开发系数gamma = 0.2 # 最优个体扰动系数for t in range(MaxIter):X_mean = np.mean(X, axis=0)# 3. 选择探索个体(公式6)k = int(np.ceil(PopSize * np.random.uniform(0.1, 0.3)))explore_idx = np.random.choice(PopSize, k, replace=False)# 4. 上蜃景策略(全局探索)for i in explore_idx:if np.random.rand() < 0.5: # 场景1:入射光左侧h = np.linalg.norm(X[i] - X_best)X[i] += h * np.random.uniform(-1, 1) * (ub - lb)else: # 场景2:入射光右侧(满足β < α < π/2)dist = np.linalg.norm(X[i] - X_best) + 1e-6step = lambda_ * (f[i] - f_best) / dist * (X[i] - X_best)X[i] += step# 5. 下蜃景策略(局部开发)for i in range(PopSize):if i != best_idx: # 普通个体dist = np.linalg.norm(X[i] - X_best) + 1e-6step = beta * f[i] / dist * (X_best - X[i])X[i] += stepelse: # 最优个体dist = np.linalg.norm(X[i] - X_mean) + 1e-6step = gamma * f[i] / dist * (X_mean - X[i])X[i] += step# 6. 边界检查X = np.clip(X, lb, ub)# 7. 更新适应度和最优解f = np.array([fobj(x) for x in X])current_best_idx = np.argmin(f)if f[current_best_idx] < f_best:f_best = f[current_best_idx]X_best = X[current_best_idx].copy()# 8. 记录收敛曲线cg_curve[t] = f_bestreturn X_best, f_best, cg_curve# 测试函数:Sphere函数(最小值0,在x=0处)
def sphere(x):return np.sum(x**2)# 运行MSO
X_best, f_best, cg_curve = MSO(sphere, dim=10, lb=-10, ub=10)
print(f"最优解:{X_best.round(4)}")
print(f"最优适应度:{f_best:.6f}")七、总结与进阶方向
MSO 作为 2025 年的前沿算法,凭借 “物理灵感 + 双策略优化” 的创新设计,在复杂优化问题中表现碾压传统算法。它不仅逻辑直观、公式简洁,还能无缝适配机器学习调参、工程优化、路径规划等多个场景,是科研和工程实践的 “利器”。
进阶优化方向
- 动态调整参数:根据迭代阶段自适应调整 λ、β、γ,进一步提升收敛速度。
- 融合局部搜索算法:结合 Nelder-Mead 单纯形法,增强局部开发精度。
- 多目标扩展:将单目标优化扩展为多目标(如同时最小化路径长度和能耗)。
这篇干货已经把 MSO 的原理、公式、代码、案例全扒透了,收藏起来,下次做优化任务直接上手!
文献参考
Jiahao He, Shijie Zhao, Jiayi Ding, Yiming Wang,
Mirage search optimization: Application to path planning and engineering design problems,
Advances in Engineering Software, Volume 203, 2025, 103883, ISSN 0965-9978, https://doi.org/10.1016/j.advengsoft.2025.103883.
(https://www.sciencedirect.com/science/article/pii/S0965997825000213)
Abstract: In this article, a new meta-heuristic optimization algorithm motivated by mirage physical principles, named Mirage Search Optimization (MSO), is proposed. MSO mainly consists of two updating strategies, i.e., the superior mirage strategy and the inferior mirage strategy, which results in the global exploration and local exploitation capabilities, respectively. In addition, other two population evolution-guided mechanisms such as the fitness-distance balance (FDB) and fitness-distance constraint (FDC) are incorporated into MSO and termed as FDB-MSO and FDC-MSO, to further check and test the good optimization performance of MSO and its variants. MSO and 25 comparison algorithms are examined on CEC2017, CEC2014 and 21 classical benchmark functions. Optimization efficiency of MSO was verified by Wilcoxon rank sum test, Friedman test and stability analysis. Furthermore, competitiveness of MSO in solving real-world problems under constraints is demonstrated using six classical engineering problems. Finally, MSO is used for the path planning problem, which verifies applicability of MSO to real-world problems. Experimental results indicate MSO is competitive with other competing algorithms. Source codes of MSO are publicly available at https://www.mathworks.com/matlabcentral/fileexchange/180042-mirage-search-optimization.
Keywords: Meta-heuristic; Mirage search optimization; Benchmark function; Engineering design; Path planning
