leetcode 474

474: 一和零

思路：0-1背包问题，选or不选（dp动态规划）

dp[i][j]：“在最多使用 i 个 0 和 j 个 1 的前提下，能够选出的最大子集大小（物品件数）”

实例：

   ...

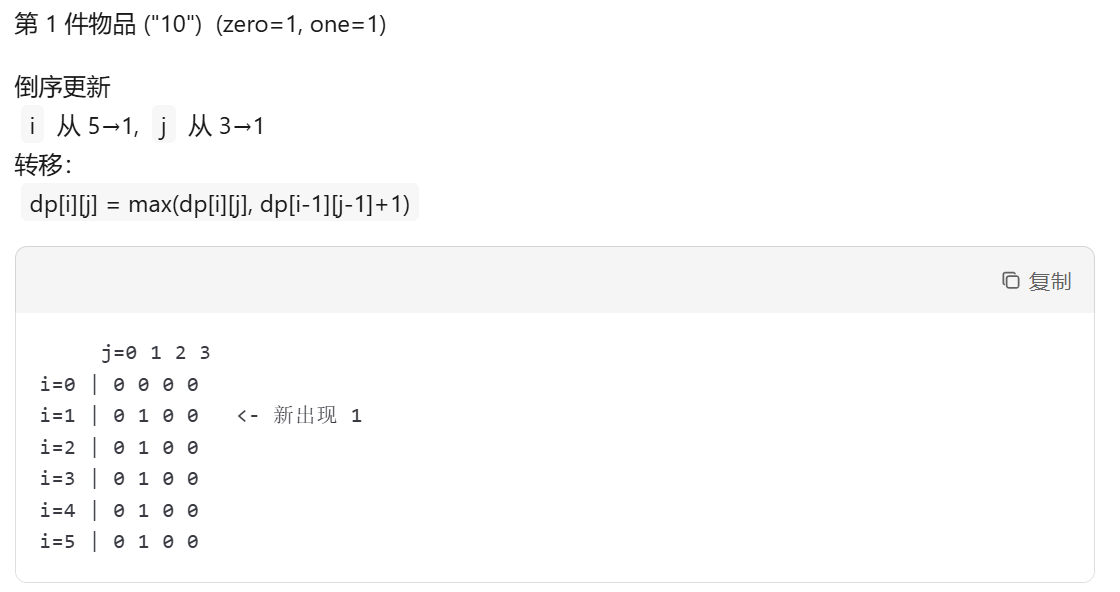
此时 dp[0][3]=3，意思“只耗 0 个 0、3 个 1最多能选 3 件”。

• 0-1 背包（每件只能拿一个）→ 倒序

• 完全背包（每件可以拿无限次）→ 正序

本题是“选 or 不选”每个字符串，典型的 0-1 背包，所以必须倒序。

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1,0));  // m个0, n个1for(auto &s :strs){int zero=count(s.begin(),s.end(),'0');int one=s.size()-zero;for(int i=m;i>=zero;i--){for(int j=n;j>=one;j--){dp[i][j]=max(dp[i][j],dp[i-zero][j-one]+1); //递归}}}return dp[m][n];}
};

可以得到消耗m个0，n个1，最多可选的字符串数目。