当前位置：首页 > news >正文

双指针：算法新手的第一道砍

news 2025/11/12 10:28:48

文章目录

前言

介绍

题目一：移动零

1.题目解析

2.算法原理

3.代码编写

题目二：快乐数

1.题目解析

2.算法原理

3.代码编写

题目三：有效三角形的个数

1.题目解析

2.算法原理

3.代码编写

题目四：三数之和

1.题目解析

2.算法原理

3.代码编写

总结

前言

本篇文章是用来记录我学习算法中双指针算法，方便我日后进行复习。欢迎大家来阅读，如有不足的地方请在评论区指出。

介绍

在算法中，双指针是一种常见且高效的基础方法，核心思路是通过两个指针（或索引）协同遍历数组、链表等线性数据结构，替代嵌套循环以优化时间复杂度。它能将暴力枚举方法需要的复杂度O (n²) 简化为 O (n)，大幅提升运行效率，空间复杂度常为 O (1)。

根据遍历方向，双指针可分为同向指针和相向指针，常见应用有用快慢指针找链表环和反转字符串等。因其逻辑直观、实现简洁，它既是算法入门的核心知识点，也是面试与工程实践中解决线性结构问题的 “常用工具”。

题目一：移动零

题目链接：移动零

1.题目解析

看完题目并结合例子，我们可以看出此题需要我们把非零元素按原来的顺序往前移，零元素就往后移，就变成[1 , 3 ,12, 0, 0]

2.算法原理

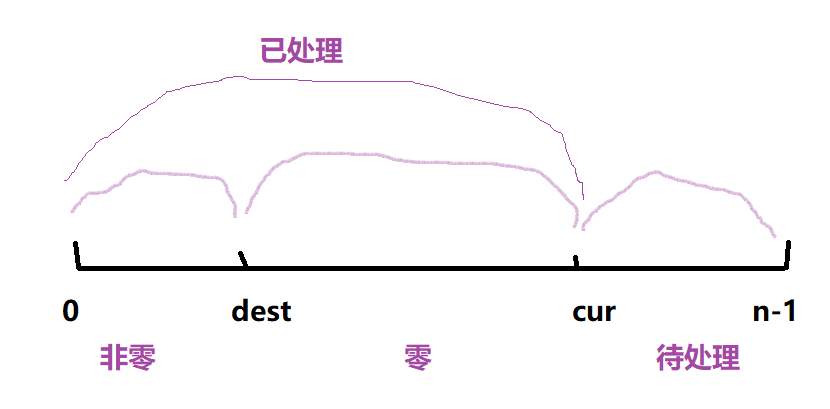
这道题可以看成“数组划分”一类，把非零元素归非零区间，零元素归零区间。在遍历元素时，我们可以用双指针来对数组进行遍历，建立俩个同方向的指针来充当下标。

两个指针的作用和范围：

1.作用：

cur：从左往右遍历数组

dest:一个划区间的分线，划分非零区间和零区间。通常在非零区间中的非零元素的最后一个位置

2.范围：

结合指针的作用，轻易推出俩个指针所划分的范围

有三个区间：

[0,dest] [dest+1,cur-1] [cur,n-1]

| | |

非零区间零区间待处理元素

如何实现

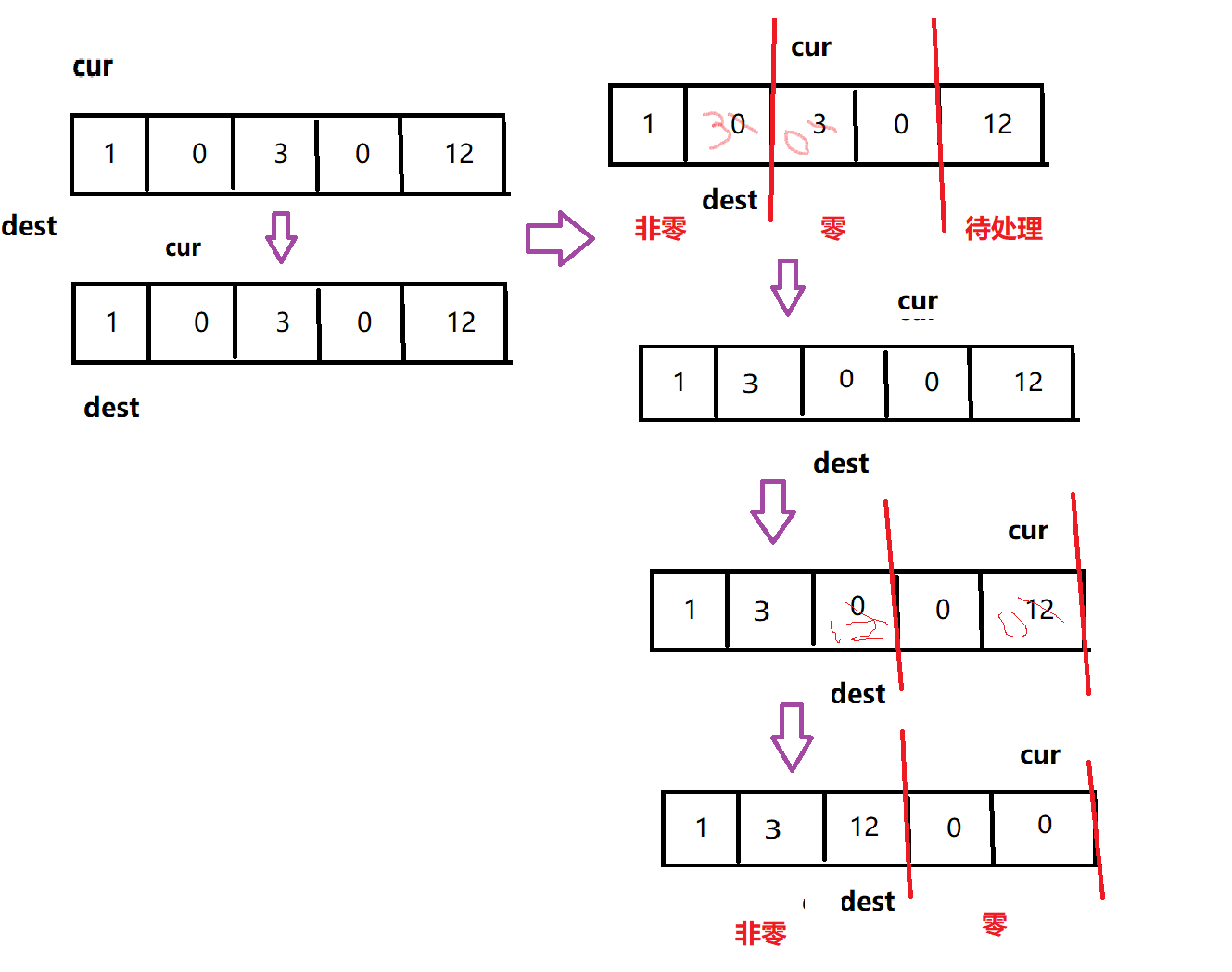
让cur从下标0左往右开始遍历，dest从下标-1开始

当cur走到‘0’，dest走到‘1’，不需要交换，直接cur++

当cur走到‘3’，用把dest+1下标的元素与cur交换，在dest++,cur++

当cur走到‘0’，用把dest+1下标的元素与cur都是0元素，不需要交换，cur++

当cur走到‘12’，用把dest+1下标的元素与cur交换，dest++，而cur++走到数组n位置越界就终止遍历，此时遍历结束

3.代码编写

class Solution {
public:void moveZeroes(vector<int>& nums) {for(int cur=0,det=-1;cur<nums.size();cur++){if(nums[cur]!=0){swap(nums[++det],nums[cur]);}}}
};

题目二：快乐数

题目链接：快乐题目数

1.题目解析

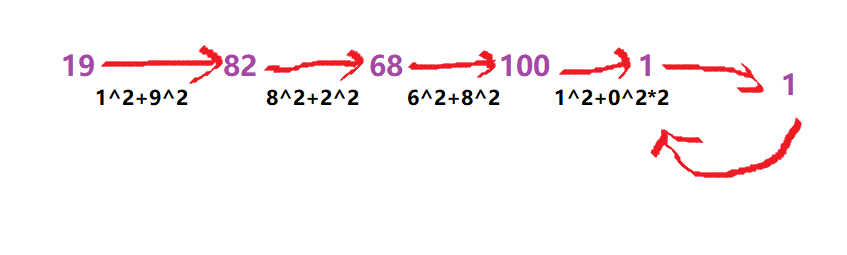
看完题目并结合例子，从画图可以联想到快慢指针的方法；慢指针走1步快指针走2步，当慢指针的值为1时，就可以判断该数为快乐数。

eg:正整数19是否为快乐数==》是

eg:正整数2是否为快乐数==》不是

2.算法原理

通过上面的画图，我们可以先把过程看成一个链表，判断链表是否有环，但是如果该数为快乐数我们也可以把此过程看成一个带环链表，相当于是一直在值1处不断地循环；让慢指针走1步，快指针走2步，当快慢指针相遇并且慢指针值为1时就判断该数是快乐数。

步骤过程：

a.确定快乐数的定义：

快乐数是对于一个正整数，不断将其替换为 “各位数字的平方和”，若最终能得到 1，则为快乐数；若进入不包含 1 的循环，则不是快乐数。

b.计算快乐数

c.遍历循环并判断是否为快乐数：

初始快慢指针-->循环移动快慢指针直至相遇-->判断相遇结果是否为1

3.代码编写

class Solution {
public:int cycleNums(int n){int sum=0;while(n){int t=n%10;sum+=t*t;n/=10;}return sum;}bool isHappy(int n) {int slow=n,fast=cycleNums(n);while(slow!=fast){slow=cycleNums(slow);fast=cycleNums(cycleNums(fast));}return slow==1;}
};

题目三：有效三角形的个数

题目链接：有效三角形的个数

1.题目解析

看完题目并结合例子，需要任意两条边之和大于第三条边才是三角形

2.算法原理

根据三角形的任意两边之和大于第三条的定义。因为最大的数+较小的数之和是一定大于另外一个较小的数，所以只需判断给定的一堆数里面较小的两个树之和大于最大的数即可。

有两种解法，暴力枚举和双指针解法。

采用暴力枚举就是遍历循环三次再进行判断，但是这样时间复杂度是O(n^3)，时间复杂度太大不够高效。

所以我们利用单调性结合使用双指针算法来解决问题，在对数组进行遍历前我们要先对数组进行有序的排序，提高效率。

解法：

1.先对乱序的数组进行有序的排序后，开始从后往前遍历找到数组中最大的数n

2.创建俩个指针，让left从下标为0开始，right从i-1位置开始。当left+right>n，说明2+9>10能成为一组三角形，用ret来计数，再让right-- ；当left+right<n,就left--

3.不断循环第二步的操作，止到越界就结束，最后返回计数的ret

3.代码编写

class Solution {
public:int triangleNumber(vector<int>& nums) {//1.优化：对数组先进行有序排序sort(nums.begin(),nums.end());int ret=0,n=nums.size();//2.用双指针，在数组中进行遍历for(int i=n-1;i>=2;i--)//找到最大数{//利用三角形三边关系和排序数组的特性高效统计有效三元组。int left=0,right=i-1;while(left<right){if(nums[left]+nums[right] > nums[i]){ret+=right-left;right--;}else{left++;}}}return ret;}
};

题目四：三数之和

题目链接：三数之和

1.题目解析

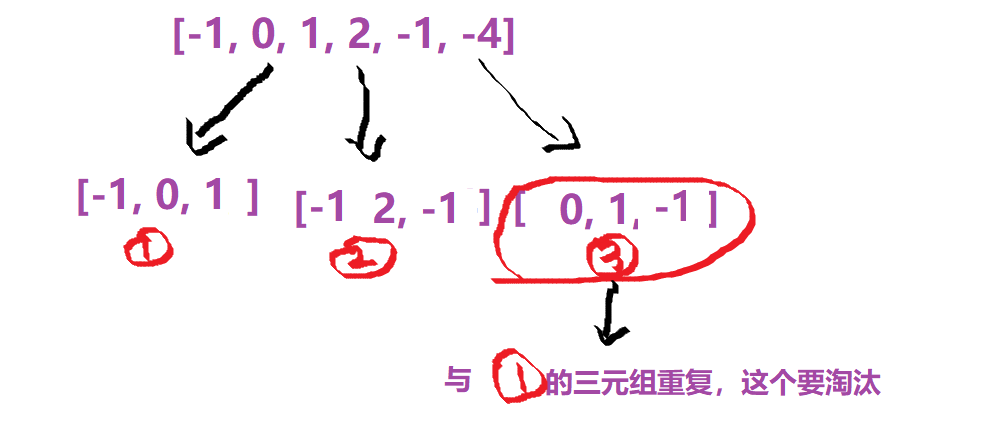
阅读完这道题大概不太能理解，仔细看玩例子会清楚知道题目的要求。题目要求在一组整数组中，找到三个数组成三元组，这一组中三个数之和为0，并且出现的三元组不能有重复的。

2.算法原理

有两种解法，解法一为先排序再进行暴力枚举最后利用set去重，但是依旧是时间复杂度不够最优；解法二先排序再用双指针方法。下面采用解法二来解答此题

需要注意细节的问题，在数组中，我们对区间中重复出现的数要进行跳过，并且不要遗落遍历数组时，重复出现的“固定的数a”，也要进行跳过；这样就可以排除重复出现的三元组。

3.代码编写

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;// 1.排序sort(nums.begin(),nums.end());// 2.用双指针解法int  n = nums.size();for(int i=0;i<n;) //固定一个数a{int left=i+1,right=n-1,target=-nums[i];while(left<right){int sum = nums[left] + nums[right];// 当区间中俩数之和大于目标数if(sum>target){right--;}// 当区间中俩数之和小于目标数else if(sum<target){left++;}else{//把得到的三元组放进ret中ret.push_back({nums[i],nums[left],nums[right]});left++,right--;//去重操作//当区间第一个数和第二数一样就去掉，left++ ;防止在区间中越界while(left<right && nums[left]==nums[left-1]){left++;}while(left<right && nums[right]==nums[right+1]){right--;}}}//遍历数组中，找固定的数也会有重复现象，所以也要去重i++;while(i<n && nums[i]==nums[i-1]){i++;}}return ret;}
};