CANN中MmDeqSwigluQuantMmDeq算子模型的深层解析

一、MmDeqSwigluQuantMmDeq算子模型解析

MmDeqSwigluQuantMmDeq 是为大语言模型（LLM）高效推理定制的量化感知复合算子，由 “矩阵乘（Mm）- 反量化（Deq）-Swiglu 激活 - 量化（Quant）- 矩阵乘（Mm）- 反量化（Deq）” 等操作串联组成，核心是在保证推理精度的前提下，通过低精度计算（int8）和硬件加速大幅降低内存与计算开销，适配资源受限场景的 LLM 部署。
下面我们一起来分层次对该算子模型进行逐一解析：

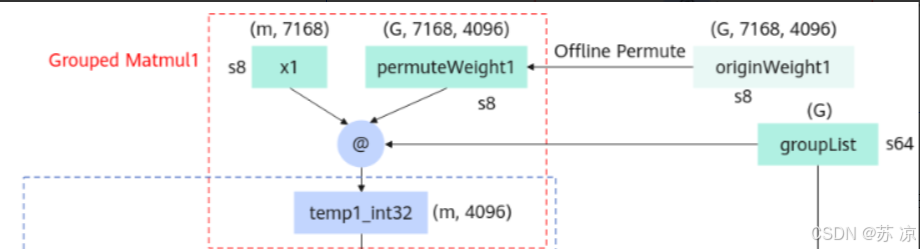
1. 1 Grouped Matmul1（分组矩阵乘法1）

• 输入：x1（s8 类型，形状 (m, 7168)）、permuteWeight1（由 originWeight1 离线置换得到，形状 (G, 7168, 4096)）、groupList（s64 类型，形状 (G)）。
• 操作：将输入按组划分后执行矩阵乘法，输出 temp1_int32（int32 类型，(m, 4096)），再转换为 float 类型的 temp1。
• 作用：通过分组计算和低精度（int8）优化矩阵乘法的效率，减少内存带宽和计算开销。

---

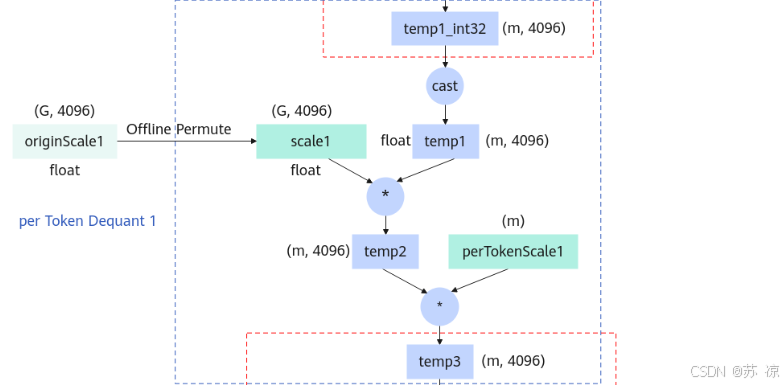
1.2 Per Token Dequant 1（逐token反量化1）

• 输入：temp1（float，(m, 4096)）、scale1（由 originScale1 离线置换得到，float 类型 (G, 4096)）、perTokenScale1（float，(m)）。
• 操作：temp1 与 scale1 逐元素相乘得到 temp2，再与 perTokenScale1 相乘得到 temp3。
• 作用：将量化后的矩阵乘法结果反量化为浮点型，并逐token（每个样本token）调整缩放，恢复数据精度。

---

1.3 Swiglu（激活函数模块）

• 输入：temp3（float，(m, 4096)）。
• 操作：
  • chunk 操作将 temp3 分为 temp4 和 gate（均为 float 类型，(m, 2048)）。
  • gate 经过 sigmoid 激活得到 temp4_sig，temp4 与 temp4_sig 相乘后，再与 gate 进一步运算得到 temp6（float，(m, 2048)）。
• 作用：实现 Swiglu 激活函数（GLU 激活的变体），引入非线性变换，增强模型对复杂模式的表达能力，是 LLM 中 MLP 层的典型操作。

---

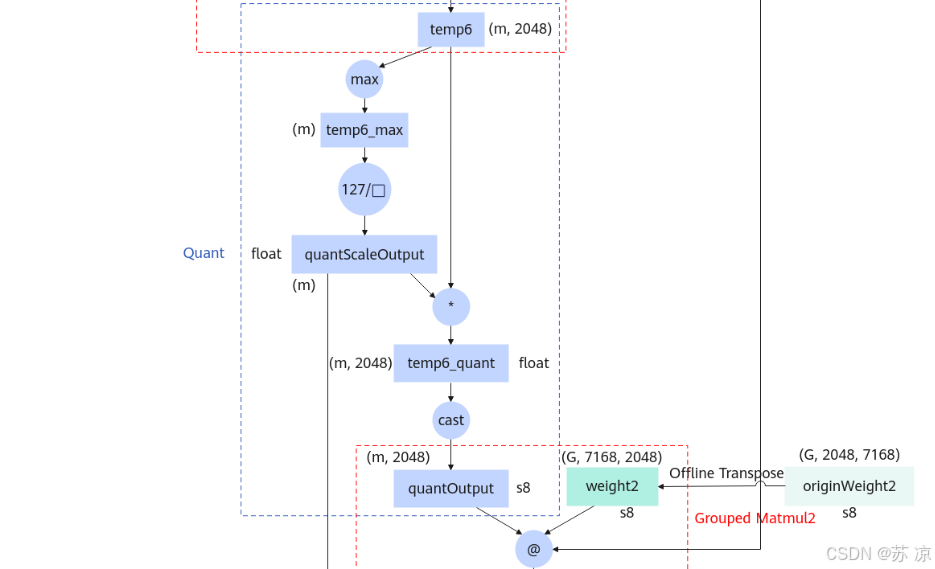
1.4 Quant（量化模块）

• 输入：temp6（float，(m, 2048)）。
• 操作：
  • 对 temp6 逐token取最大值得到 temp6_max（float，(m)）。
  • 计算 127 / temp6_max 得到 quantScaleOutput（float，(m)），temp6 与该缩放因子相乘后转换为 s8（int8）类型的 quantOutput。
• 作用：将浮点中间结果量化为 int8，大幅减少内存占用和后续计算的硬件开销；通过逐token缩放保证量化精度。

---

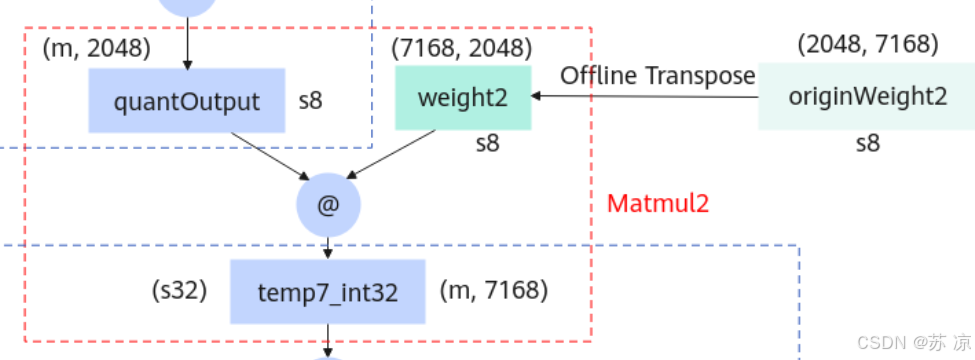
1.5 Grouped Matmul2（分组矩阵乘法2）

• 输入：quantOutput（s8，(m, 2048)）、weight2（由 originWeight2 离线转置得到，s8 类型 (G, 7168, 2048)）。
• 操作：分组矩阵乘法，输出 temp7_int32（int32 类型，(m, 7168)），再转换为 float 类型的 temp7。
• 作用：与 Grouped Matmul1 同理，通过低精度分组计算进一步优化效率。

---

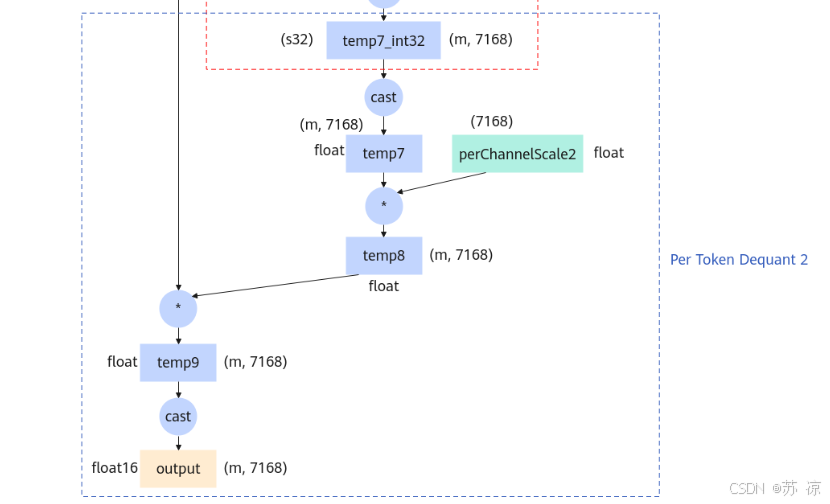
1.6 Per Token Dequant 2（逐token反量化2）

• 输入：temp7（float，(m, 7168)）、perChannelScale2（float，(G, 7168)）。
• 操作：temp7 与 perChannelScale2 逐元素相乘后，再与前文中间结果运算，最终转换为 float16 类型的 output。
• 作用：将第二次分组矩阵乘法的结果反量化，输出浮点型（float16）最终结果，平衡性能与精度。

二、在CANN中的作用

1. 昇腾硬件原生加速算子中的 “矩阵乘（Mm）” 可直接映射到昇腾 AI Core 的矩阵计算单元（Matrix Unit），利用其高并行矩阵运算能力（如 INT8 矩阵乘的高 TOPS 性能）；Swiglu 激活、量化 / 反量化的逐元素操作则由向量计算单元（Vector Unit） 加速，通过向量化指令减少循环开销，充分释放硬件算力。
2. 量化感知的精度 - 性能平衡CANN 的量化工具链（ATC+TBE） 为该算子提供端到端量化支持：

• 离线阶段（模型转换时），ATC 会提前完成权重置换（Offline Permute/Transpose）等静态操作，避免推理时的动态开销；
• 推理阶段，算子的 INT8 计算原生适配昇腾硬件的低精度单元，同时通过 “逐 token 缩放（perTokenScale）”“逐通道缩放（perChannelScale）” 实现精度补偿，在低精度计算的高性能与浮点输出的精度需求间取得平衡。

3. TBE 算子融合与定制优化通过 CANN 的TBE（Tensor Boost Engine）算子开发工具，可将 “矩阵乘 - 反量化 - Swiglu - 量化 - 矩阵乘 - 反量化” 的多步骤流程融合为单个 TBE 算子，减少数据搬运次数（降低访存瓶颈），并支持计算图裁剪、算子内联等深度优化，让流程以 “近硬件原生” 的方式执行。
4. 异构调度的可扩展性CANN 的异构任务调度机制可将算子的不同阶段（矩阵乘、Swiglu、量化）分配到昇腾 AI Core 的不同计算单元，实现计算流水线重叠；同时支持多芯（多 AI Core）、多卡（多 Ascend 设备）的分布式并行调度，为大批次、大模型的 LLM 推理提供可扩展的性能支持。

MmDeqSwigluQuantMmDeq 算子在 CANN 中，是将大语言模型推理的 “量化 - 计算 - 激活” 全流程与昇腾硬件深度绑定，通过硬件级并行、算子融合、量化感知优化，实现 “高性能（低延迟、高吞吐）+ 高精度” 的 LLM 推理能力，是昇腾平台在大模型轻量化部署场景下的核心技术载体之一。