深度学习(2)—— 神经网络与训练
1.从神经元到感知机
想象一下,你的大脑里有860亿个"快递站点"——神经元。每个站点长得像个怪异的树杈子:中间一个圆鼓鼓的细胞体(像个仓库),顶上分叉出无数"树枝"(树突),底下一根长长的"传送带"(轴突)。当神经元"兴奋"时,它会做一件超酷的事:从传送带末端喷出一堆化学物质(神经递质),像快递包裹一样,扔给下一个站点的树枝。这些包裹可不是乱飞的——它们有"重量",有的兴奋("快开门!营业啦!"),有的抑制("关门下班!")。
而在上世纪50年代,有个叫罗森布拉特的哥们儿盯着神经元结构看了半天,一拍大腿:"我去,这不就是个天然的计算模型吗?"于是有了下面最为基础的神经元模型!
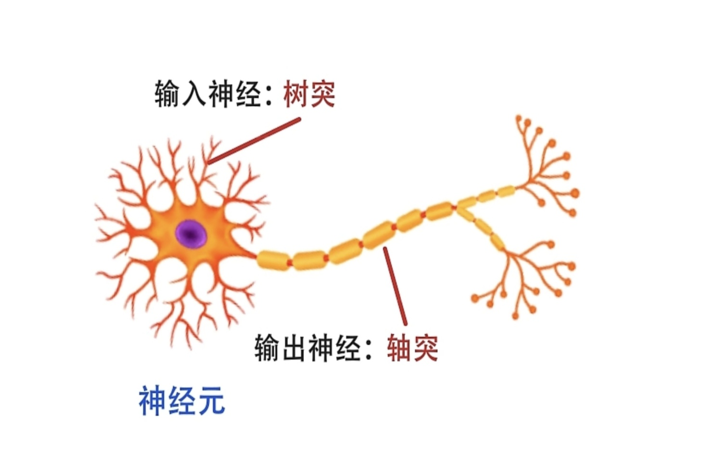
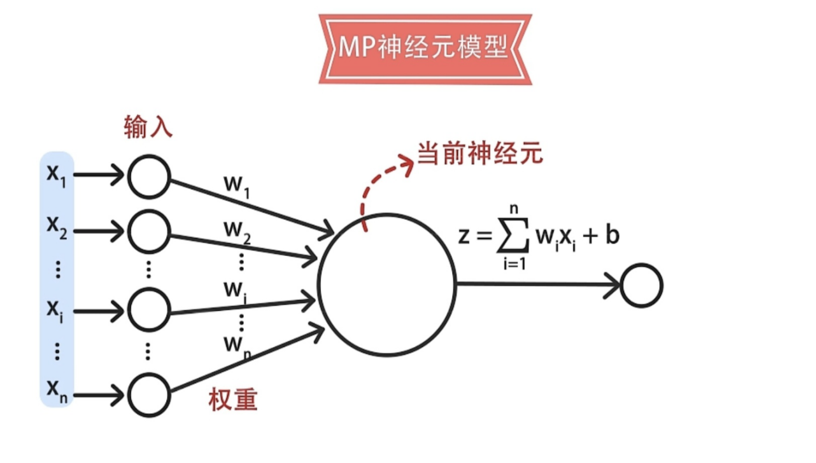
神经元接收来自其它n个其它神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元将接收到的总输入值将与神经元的阈值进行比较,然后通过激活函数处理以产生神经元的输出。
而在抽象出神经元的计算模型的基础上,罗森布拉特创造了世界上第一个人工神经元网络,感知机。感知机由两层神经元组成,是一种基础的二分类模型,其训练过程是基于梯度下降算法,基本原理是通过对输入的特征向量进行线性加权和,再加上一个阈值,来得到一个输出结果。
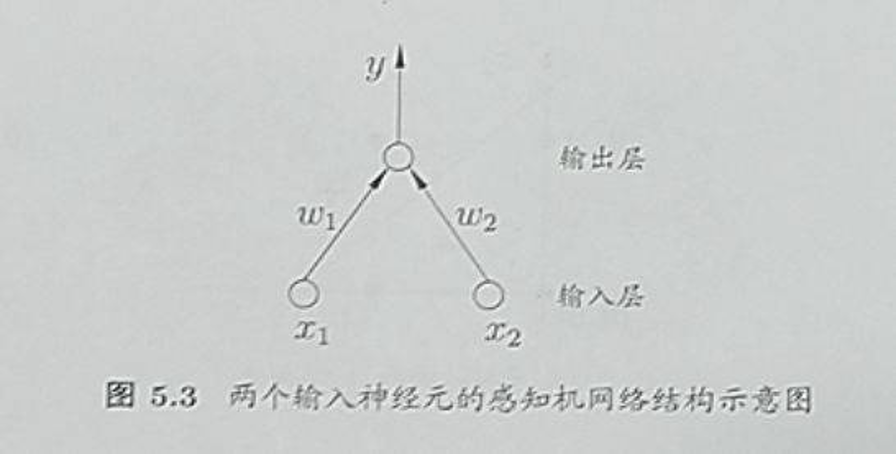
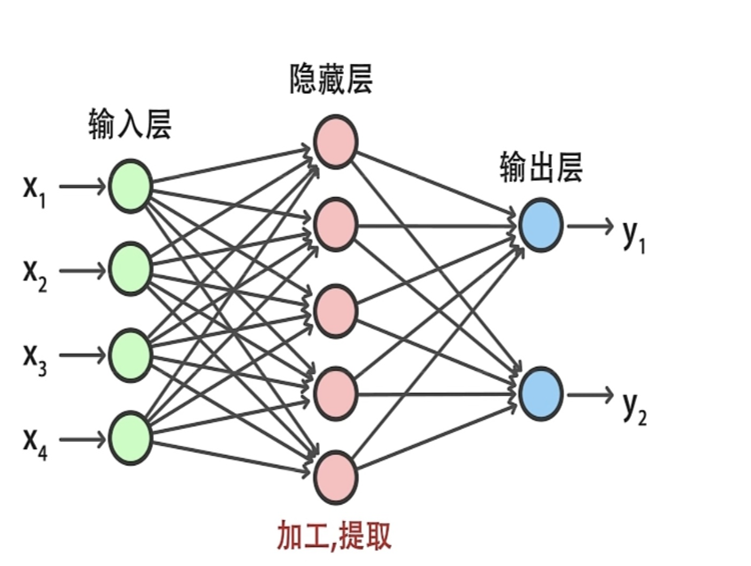
而如果采取了多个神经元模型进行组合,这便有了多层感知机(MLP),它是一种简单的前向人工神经网络模型,一般可分为三层,输入层,隐藏层,输出层。也就有了我们如今人工神经网络的基本结构!
| 对比维度 | 感知机 (Perceptron) | 多层感知机 (MLP - Multilayer Perceptron) |
|---|---|---|
| 结构特点 | 单层神经元网络,仅含输入层和输出层 | 至少包含一个隐藏层的三层或以上网络 |
| 网络层数 | 2层(输入层 + 输出层) | ≥3层(输入层 + 隐藏层 + 输出层) |
| 激活函数 | 通常使用阶跃函数(Step Function) | 使用非线性激活函数(ReLU, Sigmoid, Tanh等) |
| 决策边界 | 只能学习线性决策边界 | 可学习非线性、复杂的决策边界 |
| 学习能力 | 仅能处理线性可分问题(如与、或、非) | 可处理线性不可分问题(如异或XOR) |
| 局限性 | 无法解决非线性问题,功能受限 | 可能面临梯度消失、过拟合等问题 |
| 训练算法 | 感知机学习规则(简单权重更新) | 反向传播算法(Backpropagation) |
| 权重更新 | 基于单个样本错误驱动 | 基于梯度下降,使用整个数据集或批次 |
| 计算复杂度 | 低,训练速度快 | 较高,训练时间长,需要更多计算资源 |
| 典型应用 | 简单的二分类任务、线性回归 | 图像识别、自然语言处理、复杂模式识别 |
| 表达能力 | 弱,相当于线性分类器 | 强,可逼近任意连续函数(万能逼近定理) |
2.神经网络分析
我们不妨举个例子,假设我们知道了某种零件的长度和宽度,想要预测该零件的使用寿命。
理论上两层神经网络已经可以拟合任意函数,所以我们完全可以构建如下的一个神经网络:
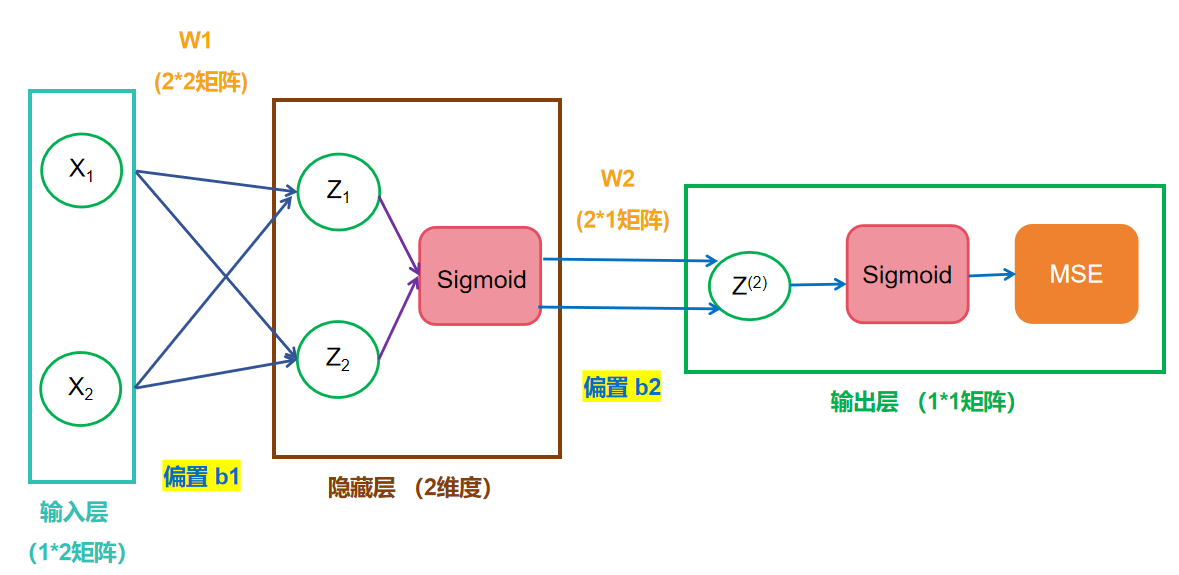
在这神经网络当中,我们输入包括长度和宽度,两个特征,所以输入的是一个1*2的矩阵X;而连接输入层和隐藏层的是W1(权重)和b1(偏置),我们完全可以根据仿射变换,进行计算,得到隐藏层中Z的结果,公式如下,其实就是简单的线性代数的计算:
同样的对于连接隐藏层和输出层的W2和b2,也是同样的计算。如果你还对线性代数的计算有印象的话,应该会知道:一系列线性方程的运算最终都可以用一个线性方程表示。这样神经网络就失去了意义,因为现实生活中大部分情况下,都是非线性关系。为此,我们引入了激活层。
2.1 激活层
简而言之,激活层是为矩阵运算的结果添加非线性的。常用的激活函数如下:
| 激活函数 | 公式 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| Sigmoid | 1. 输出平滑,在(0,1)之间 2. 易于求导 | 1. 梯度消失:在饱和区梯度接近于0 2. 输出不是零中心的 3. 指数计算较慢 | 二分类问题的输出层;历史模型;不应再用于隐藏层 | |
| Tanh | 1. 输出是零中心的 (-1, 1) 2. 在实践中通常优于Sigmoid | 同样存在梯度消失问题 | RNN 的隐藏层;在实践中有时代替Sigmoid | |
| ReLU | 1. 在正区间解决了梯度消失问题 2. 计算速度极快 3. 收敛速度比Sigmoid/Tanh快 | 1. Dying ReLU:负数部分梯度为0,导致神经元“死亡”且无法恢复 2. 输出不是零中心的 | 目前最常用的默认激活函数,尤其用于CNN和大多数深度前馈网络的隐藏层 | |
| Leaky ReLU | α是一个很小的值 | 1. 解决了 Dying ReLU 问题 2. 保留了ReLU的所有优点 | 1. 结果不总是一致:超参数 𝛼α 需要选择 2. 在负区间是线性的,可能不满足“激活”的直觉 | 当担心出现“死亡神经元”时,可替代ReLU;表现有时优于ReLU |
| Parametric ReLU (PReLU) | α是一个可学习参数 | 1. 将负区间的斜率 α 作为可学习参数,更具灵活性 2. 在大型数据集(如ImageNet)上表现优异 | 1. 有额外的计算和参数 | 大型模型和数据集(如图像分类);当需要模型自己学习最佳激活形式时 |
| Exponential LU (ELU) | α是一个超参数 | 1. 具有ReLU的所有优点 2. 输出接近零中心 3. 在负区间平滑渐近,可能比Leaky ReLU更有鲁棒性 | 1. 计算涉及指数,比ReLU慢 | 对噪声鲁棒性要求高的任务;可以替代ReLU尝试 |
| Swish (由Google提出) | β是可学习参数或常数 | 1. 平滑、非单调 2. 在实践中(尤其深层模型)经常优于ReLU 3. 被发现在视觉任务中表现很好 | 1. 计算量较大(涉及Sigmoid) | 深度卷积网络(CNN) 和图像分类任务中一个强有力的竞争者;可以替代ReLU进行实验 |
| GELU | Φ(x) 是标准高斯累积分布函数 | 1. 在Transformer模型中表现卓越 2. 结合了随机正则化的思想,是一个平滑的近似ReLU | 1. 计算相对复杂 | 自然语言处理(NLP) 领域的Transformer架构(如BERT, GPT系列)的默认激活函数 |
| Softmax | 1. 将输出转换为概率分布 2. 所有输出之和为1 | 1. 仅用于输出层 2. 对极端值敏感 | 多分类问题的输出层;将原始分数映射为类别概率 |
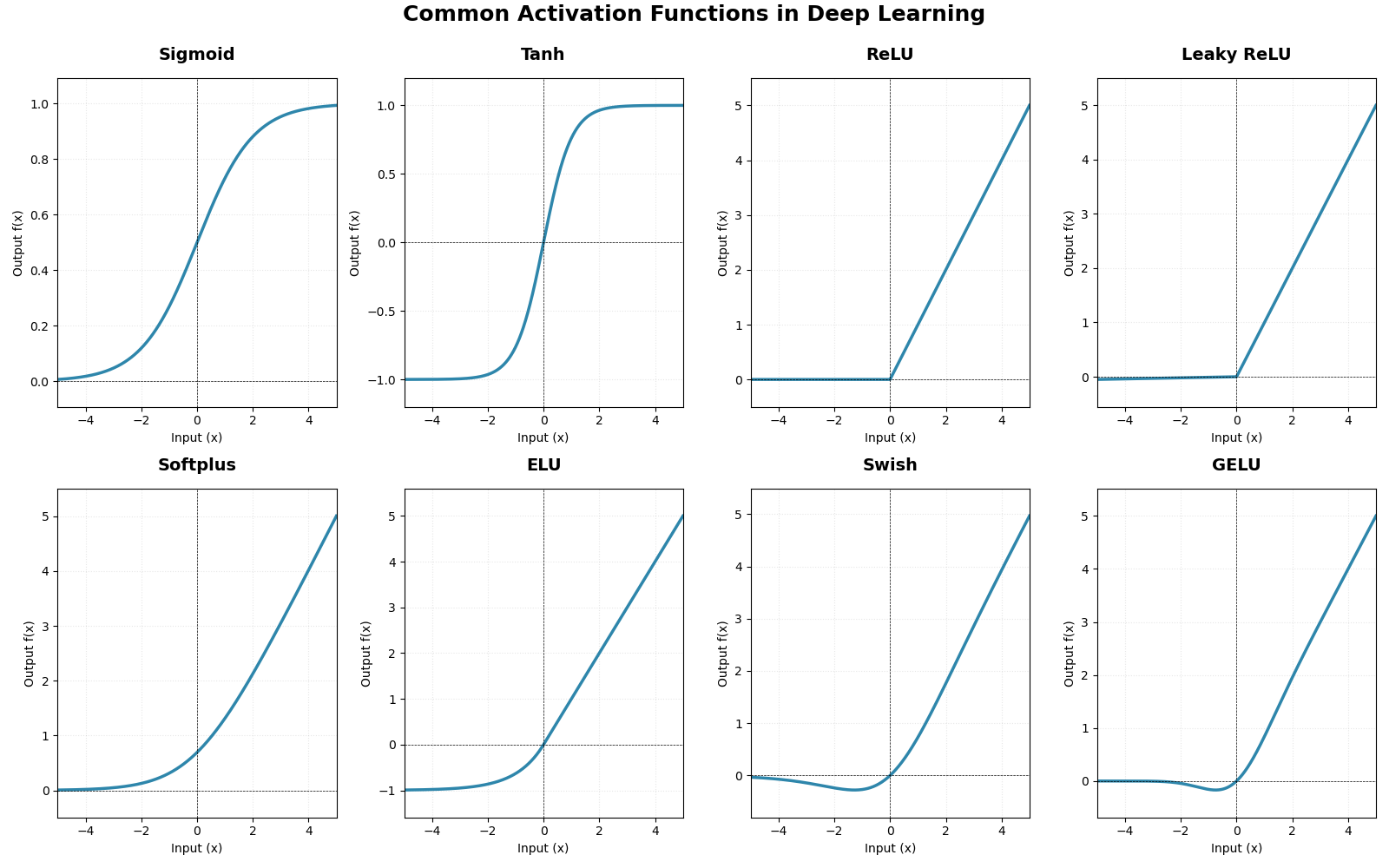
一些激活函数的图像如下所示:
2.2 前向过程

现在我们以具体数据,来说明一下,模型内部是怎么计算的:
假定我们输入的特征矩阵为 [0.1, 0.2],模型的 初始化参数 如下:
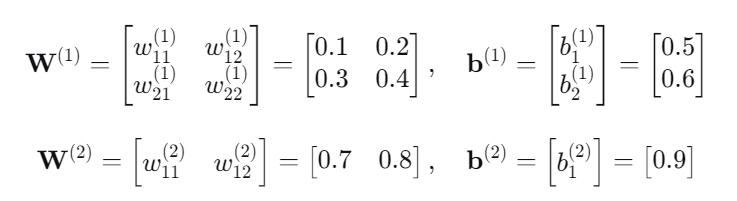
输入层 → 隐藏层:
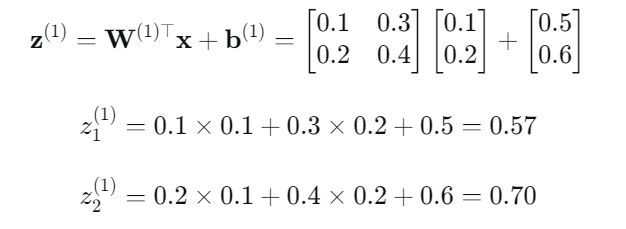
通过Sigmoid的激活层进行输出: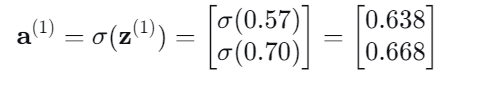
隐藏层 → 输出层:
输出层的加权输入:
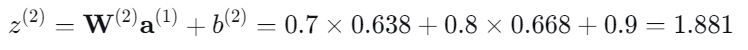
网络最终输出:
![]()
据此,我们依据当前的模型,预测出长度和宽度为0.1 ,0.2的零件,使用寿命大致为0.867年。
3. 反向传播(BP)
由上面的过程,可以知道,模型主要的参数就是W1,W2以及b1和b2。只有这几个参数具体数值不知道,其它的数值都知道。那我们该如何设置这些参数的值,使得模型预测的更准确呢 ?
实际上这些参数,并不是我们所设置的,模型最开始的时候,会随机初始化这些参数,通过对模型进行训练,让模型得以自行的调整参数,使得预测结果更为准确。举个栗子 ~,比如上面的结果,我们预测出零件的使用寿命为0.867,但实际上零件的使用寿命为1.这里就有了误差。我们使用均方误差(MSE)来表示这种误差的大小(思考一下,为什么不直接把预测值与实际值相减作为评判的误差 ?):

可以看到MSE的值越接近于0,说明我们模型的预测效果就越好。所以我们训练模型的过程,就是通过让模型自身不断调整参数,使得我们的误差变小。而我们最常用的方法就是梯度反向传播算法(BP),实际上就是随机梯度下降(SGD, Stochastic Gradient Descent)。
3.1 链式法则
假设一个场景,一辆汽车15万元,要收10%的购置税,如果要买2辆,则该过程可以画成:
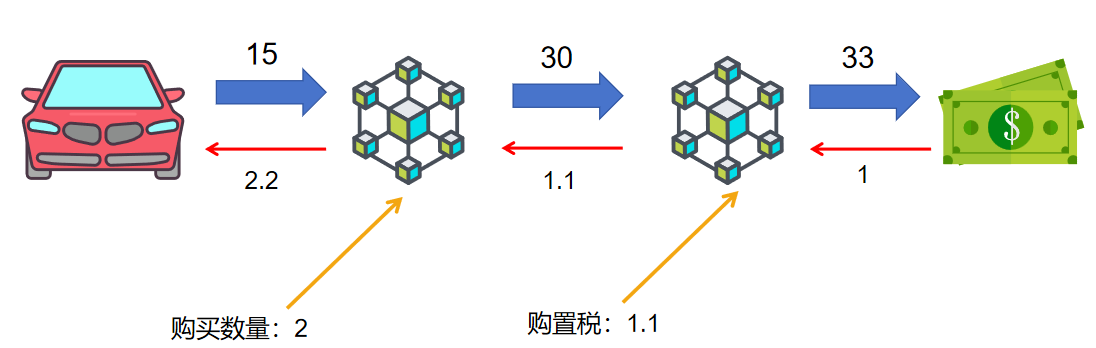
如果现在,我们想要知道汽车价格每变动1万元,对最终的价格会产生多少影响,我们很自然地就会想到求导,我们从右往左进行求导:
①33/33=1
②33/30=1.1
③30/15=2
那么最终价格相对于汽车单价的导数就是①×②×③=2.2
这就是链式法则。我们只需要知道每个节点导数值,然后求乘积就可以了。
在多元函数中,就是一个不断求偏导相乘的一个结果,如下:
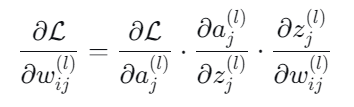
3.2 SGD和学习率
学习率就像你下山时每一步跨多大:
步子太大(学习率过高),容易跳过山谷最低点,来回震荡
步子太小(学习率过低),下山慢得要命,浪费时间
合适的步子才能又快又准地到达谷底
SGD(随机梯度下降)则是决定你怎么判断方向:
普通方法:每次站在山顶,看遍整个山坡,算出最陡的方向再走一步(慢但稳)
SGD:随机蒙住一只眼睛,只看附近一小块山坡,大致判断方向就走一步(快但不稳)
实际中常用折中版:每次看一小片区域(一小批数据),平衡速度和稳定性
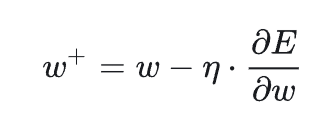
所以,当我们设置好学习率,计算出梯度的时候,就可以按照SGD(上面的公式),来更新新的参数了。
3.3完整过程

我们继续在第一次前向的过程的基础上,介绍如何更新参数(预测值为0.867,假定真实值为1):
1.使用均方误差计算损失:
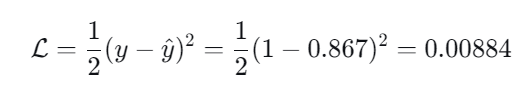
2.计算损失对于输出的梯度:
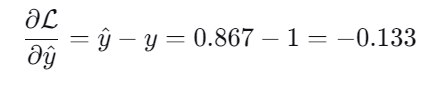
(从这里就可以看出,为什么不直接相减作为误差了,如果采取直接相减,损失对权重的导数是常数,与误差大小无关,并且可能为负值,无法衡量出“错误程度”,不知道这个值是该越大越好,还是越小越好,为了方便,规定损失函数一定是非负的!)
而对于Sigmoid函数,它的导数具有以下性质: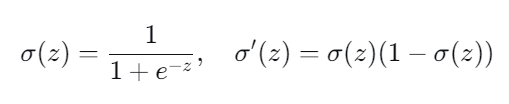
3.Sigmoid 函数导数
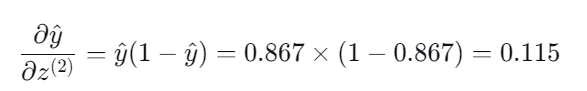
4.输出层权重梯度:
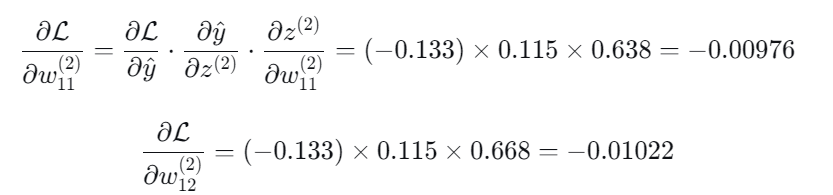
5.输出层偏置梯度:
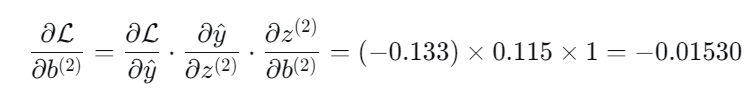
假定我们的学习率为0.5,我们此时就可以更新输出层的参数了

同样的道理,我们继续往前传播,就可以更新出隐藏层的参数了。
最终,验证,使用新的参数,在此进行前向传播,损失值确实下降了。接着我们在此重复同样的过程,从而不断更新参数,逼近最优解。
