背包dp

 

lc08.11

二维dp解决完全背包问题

 

dp[i][j] 记录前 i 种硬币凑成 j 分的表示法数量

分“不选当前硬币”和“选当前硬币”两种情况递推

最终得到 n 分的所有组合数

class Solution {
typedef long long ll;
int mod=1e9+7;
public:
int waysToChange(int n) 
{
vector<int> coins={1,5,10,25};
// dp维度：dp[硬币种类][金额]
vector<vector<ll>> dp(4, vector<ll>(n+1, 0));
// 初始化：第0种硬币（1分）凑j分的表示法
for(int j=0;j<=n;j++)
dp[0][j] = 1;

for(int i=1;i<4;i++){
for(int j=0;j<=n;j++){
dp[i][j] = dp[i-1][j]; // 不选
if(j >= coins[i]){
dp[i][j] = (dp[i][j] + dp[i][j-coins[i]]) % mod; // 选
}
}
}
return (int)dp[3][n];
}
};

 

lc624

注意到 数组已按升序排好了～

class Solution {
public:
int maxDistance(vector<vector<int>>& arrays) {
int min1 = INT_MAX, min2 = INT_MAX, minIdx1 = -1;
int max1 = INT_MIN, max2 = INT_MIN, maxIdx1 = -1;
int n = arrays.size();
for(int i=0;i<n;i++)
{
int mn = arrays[i][0];
int mx = arrays[i].back();
// 更新最小值
if(mn < min1){
min2 = min1;
min1 = mn;
minIdx1 = i;
} else if(mn < min2){
min2 = mn;
}
// 更新最大值
if(mx > max1){
max2 = max1;
max1 = mx;
maxIdx1 = i;
} else if(mx > max2){
max2 = mx;
}
}
if(maxIdx1 != minIdx1){
return max1 - min1;
} else {
return max(max1 - min2, max2 - min1);
}
}
};

 

lc1814

移项后和我的hash说去叭

class Solution {
/*
nums[i] + rev(nums[j]) == nums[j] + rev(nums[i])
*/
int mod=1e9+7;
typedef long long ll;
public:
int countNicePairs(vector<int>& nums) 
{
int n=nums.size();
ll ret=0;
vector<int> revn;
for(auto& num:nums)
{
string s=to_string(num);
reverse(s.begin(),s.end());
int t=stoi(s);
revn.push_back(t);
}
unordered_map<int,int> hash;
for(int i=0;i<n;i++)
{
if(hash[nums[i]-revn[i]]>0)
ret+=hash[nums[i]-revn[i]];
hash[nums[i]-revn[i]]++;
}
int rets=ret%mod;
return rets;
}
};

 

lc1653

继承dp

if(s[i-1]=='a')

     dp[i][0]=dp[i-1][0];

 

dp[i][1]=min(dp[i-1][0],dp[i-1][1]);//可继承a

/*
输入：s = "aababbab"
输出：2
*/

class Solution {
public:
int minimumDeletions(string s)
{
int n=s.size();
vector<vector<int>> dp(n+1,vector(2,0));
for(int i=1;i<=n;i++)
{
if(s[i-1]=='a')
{
dp[i][0]=dp[i-1][0];
dp[i][1]=dp[i-1][1]+1;//turn b
}
else
{
dp[i][0]=dp[i-1][0]+1;
dp[i][1]=min(dp[i-1][0],dp[i-1][1]);//可继承a
}
}
return min(dp[n][0],dp[n][1]);
}
};

 

lc120

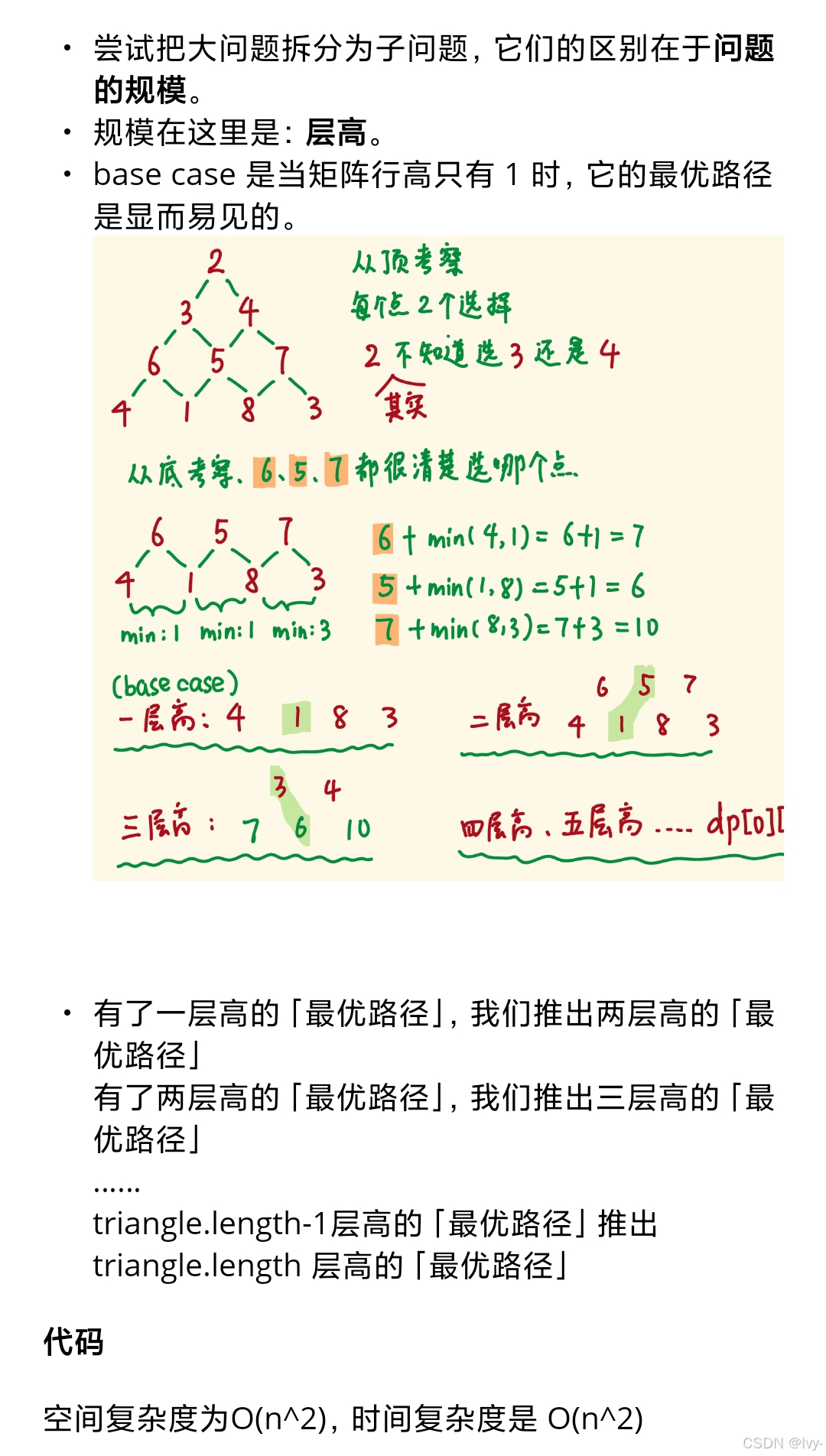
 class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n=triangle.size();
vector<int> dp(triangle[n-1].begin(),triangle[n-1].end());
for(int i=n-2;i>=0;--i)
{
for(int j=0;j<=i;++j)
{
dp[j]=min(dp[j],dp[j+1])+triangle[i][j];
}
}
return dp[0];
}
};

 

从上到下的写法

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) 
{
int n=triangle.size();
vector<vector<int>> 
dp(n,vector<int>(n,0));

dp[0][0]=triangle[0][0];
for(int i=1;i<n;i++)
{
dp[i][0]=triangle[i][0]+dp[i-1][0];
for(int j=1;j<=i;j++)
//j上限为i
{         
dp[i][j]=triangle[i][j]+
min(dp[i-1][j],dp[i-1][j-1]);

dp[i][i] = triangle[i][i] + dp[i-1][i-1]; // 补充尾元素处理
}
}
int ret=INT_MAX;
for(int i=0;i<n;i++)
{
ret=min(ret,dp[n-1][i]);
}
return ret;
}
};