GJOI 11.5 题解

1.骑行

题意

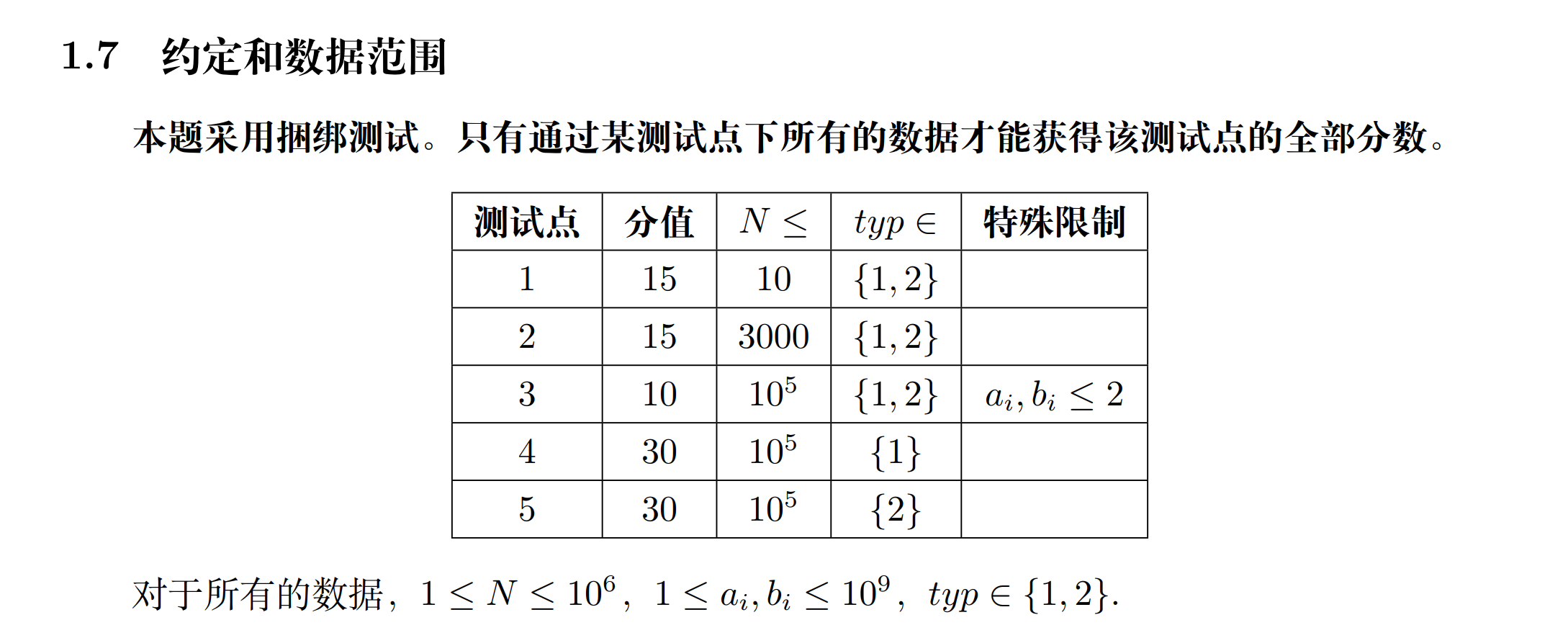
思路

求最小就两个从小到大排序，因为大的可以把大的消耗掉；最大就一个从小到大，一个从大到小，把大的优势通过小的优势体现出来。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e6+9;
ll op,n,a[N],b[N];
bool cmp(ll x,ll y)
{return x>y;
}
int main()
{freopen("cycle.in","r",stdin);freopen("cycle.out","w",stdout);scanf("%lld%lld",&op,&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);for(int i=1;i<=n;i++)scanf("%lld",&b[i]);if(op==1){sort(a+1,a+n+1);sort(b+1,b+n+1);ll ret=0;for(int i=1;i<=n;i++)ret+=max(a[i],b[i]);printf("%lld\n",ret);}else{sort(a+1,a+n+1);sort(b+1,b+n+1,cmp);ll ret=0;for(int i=1;i<=n;i++)ret+=max(a[i],b[i]);printf("%lld\n",ret);}return 0;
}

2.洛谷 P11671 USACO25JAN Farmer John’s Favorite Operation S

题意

思路

首先所有 $a_i$ 对 $M$ 取模得到 $y{s}_i$，$x$ 肯定是选在某个 $y{s}_i$ 是最优的。对所有 $y{s}_i$ 排序枚举 $x$，考虑让所有其他余数都变成 $x$ 的最少步数。

$ys\to x$ 有 $3$ 种变法：

ll choose(ll x,ll ys)
{return min({abs(x-ys)%m,abs(x-ys-m)%m,abs(x+m-ys)%m});//可以不带%m
}

分别是，直接加减，商 $-1$ 或者商 $+1$，于是容易写出 $O(n^2)$ 暴力。

考虑快速求解所有解的和。发现本质上是到 $x,x-M,x+M$ 的距离的最小值，记 $mid=\frac{M}{2}$，通过计算可得：

• $x\le mid$：三段分别为 $[0,x],(x,x+mid],(x+mid,M)$；
• $x>mid$：三段分别为 $[0,x-mid],(x-mid,x],(x,M)$。

记余数的前缀和按照对应的答案式子去做即可。写起来比较繁琐，具体细节见代码。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e5+9,inf=3e14;
ll Q,n,m;
ll a[N],ys[N];
ll pre[N];
ll choose(ll x,ll ys)
{return min({abs(x-ys)%m,abs(x-ys-m)%m,abs(x+m-ys)%m});
}
int main()
{freopen("game.in","r",stdin);freopen("game.out","w",stdout);scanf("%lld",&Q);while(Q--){scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);ys[i]=a[i]%m;}sort(ys+1,ys+n+1);for(int i=1;i<=n;i++)pre[i]=pre[i-1]+ys[i];ll ans=inf;for(int i=1;i<=n;i++){ll x=ys[i],ret=0;if(x<m/2){ret+=(i-1)*x-pre[i-1];ll mid=m/2;ll pos1=upper_bound(ys+1,ys+n+1,x+mid)-ys;ret+=(pre[pos1-1]-pre[i])-x*(pos1-1-i);ret+=(x+m)*(n-pos1+1)-(pre[n]-pre[pos1-1]);ans=min(ans,ret);}else {ret+=pre[n]-pre[i]-(n-i)*x;ll mid=m/2;ll pos2=lower_bound(ys+1,ys+n+1,x-mid)-ys;ret+=x*(i-1-pos2+1)-(pre[i-1]-pre[pos2-1]);ret+=pre[pos2-1]+(m-x)*(pos2-1);ans=min(ans,ret);}}printf("%lld\n",ans);}return 0;
}

附一个可以快速判断式子的解的取值范围的代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e5+9,inf=3e14;
ll x,m;
ll choose(ll x,ll ys)
{return min({abs(x-ys)%m,abs(x-ys-m)%m,abs(x+m-ys)%m});
}
int main()
{scanf("%lld%lld",&x,&m);for(int i=0;i<m;i++){cout<<i<<":";cout<<abs(i-x)%m<<" "<<abs(i-x-m)%m<<" "<<abs(i+m-x)%m<<endl;}return 0;
}

3.洛谷 P13785 eJOI2022 Longest Unfriendly Subsequence

题意

思路

设 $f_{i,x,y}$ 表示选到 $i$，最后的数为 $x,y$ 的最大长度。$x,y$ 可以离散化，可以不加或者加入 $a_i$，转移 $O(n^3)$：
$$\begin{array}{c}{f}_{i,x,y}\leftarrow f_{i-1,x,y}\\ f_{i,y,a_i}\leftarrow \{\begin{array}{l}{f}_{i-1,0,0}+1,y=0\\ f_{i-1,0,y}+1,a_i\ne y\\ f_{i-1,x,y}+1,a_i\ne x,y\end{array}\end{array}$$

显然可以优化掉一维，即 $f_{i,j}$ 表示最后一个选在 $i$，再上一个选在 $j$，那么枚举两个选点，时间复杂度依然 $O(n^3)$。瓶颈在枚举选点。

但是真的考虑那么多点吗？这些选点可是会包含前面的选点带来的贡献的，显然越往前面枚举答案是越劣的。所以可以限制只看前面 $k$ 个选点。$k$ 取 $5\sim 10$ 左右发现可过。

但怎么能只满足于 gei 过？不妨判断一下 $k$ 最小可以取到多少。设最后的答案为 $b_{1\sim n}$，在 $b_i\sim b_{i+1}$ 之间，最多有 $4$ 种 $\ne b_i,b_{i+1}$ 的（因为 $b_{i+1}$ 还要关联 $b_{i-1}$），来到第 $5$ 种时中间必然能再塞一个。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
using namespace std;
const ll N=2e5+9,M=6,inf=0x3f3f3f3f;
ll Q,n;
ll a[N],f[N][M],pre[N][M];
int main()
{freopen("seq.in","r",stdin);freopen("seq.out","w",stdout);scanf("%lld",&Q);while(Q--){ll tem;scanf("%lld",&tem);n=0;for(int i=1;i<=tem;i++){cin>>a[i];if(a[n]!=a[i])a[++n]=a[i];}for(int i=1;i<=n;i++){pre[i][0]=i-1;for(int j=1,k=0;j<4;k++)if(a[pre[i-1][k]]!=a[i])pre[i][j++]=pre[i-1][k];}ll ret=0;for(int i=1;i<=n;i++){for(int j=0;j<4;j++){f[i][j]=0;for(int k=0;k<4;k++)if(a[i]!=a[pre[pre[i][j]][k]])f[i][j]=max(f[i][j],f[pre[i][j]][k]+1);ret=max(ret,f[i][j]);}}printf("%lld\n",ret);}return 0;
}

附一个自认为对但是挂了的“正解”。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const ll N=2e5+9,M=11,inf=0x3f3f3f3f;
ll Q,n;
ll a[N],f[N][M];
int main()
{freopen("seq.in","r",stdin);freopen("seq.out","w",stdout);scanf("%lld",&Q);while(Q--){scanf("%lld",&n);ll tem=n;n=0;for(int i=1;i<=tem;i++){scanf("%lld",&a[i]);if(a[n]!=a[i])a[++n]=a[i];}ll ret=1;memset(f,-inf,sizeof(f));f[0][0]=0;for(int i=1;i<=n;i++){f[i][0]=1;for(int j=1;j<=6&&i-j>=1;j++){if(a[i]!=a[i-j])f[i][j]=max(f[i][j],f[i-j][0]+1);}for(int j=1;j<=6&&i-j>=1;j++){for(int k=1;k<=6&&i-j-k>=1;k++){if(a[i]!=a[i-j]&&a[i]!=a[i-j-k]){f[i][j]=max(f[i][j],f[i-j][k]+1);}}ret=max(ret,f[i][j]);}}printf("%lld\n",ret);}return 0;
}

4.洛谷 P10764 BalticOI2024 Wall