当前位置：首页 > news >正文

复杂网络入门到精通5：网络动力学

news 2025/11/12 8:18:17

本文为《复杂网络仿真入门到精通》系列第5篇。
前几篇主要介绍了网络的结构特征，这一篇我们将正式进入网络动力学领域——让网络“动”起来。

系列文章：

系列合集
下一篇预告：网络鲁棒性分析

给大家推荐一个在线复杂计算平台, 欢迎大家进行体验
复杂网络分析平台

支持：

AI 智能报告生成上传邻接矩阵文件；
自动构建网络, 指标一键计算与可视化；
网络鲁棒性分析（节点/边攻击）
级联失效模型分析

一、什么是网络动力学？

网络动力学研究的是：

在一个由节点和边组成的系统中，状态如何随时间演化。

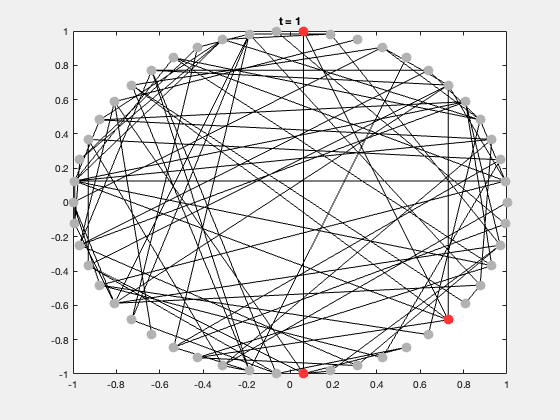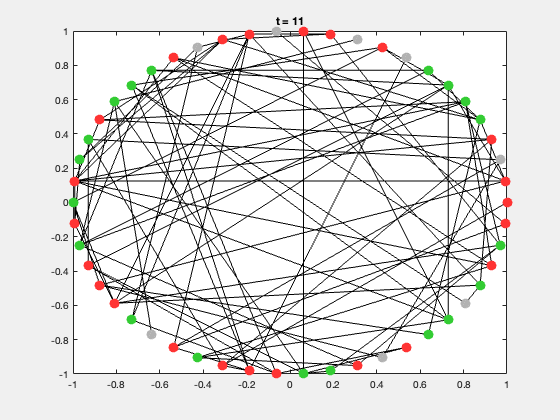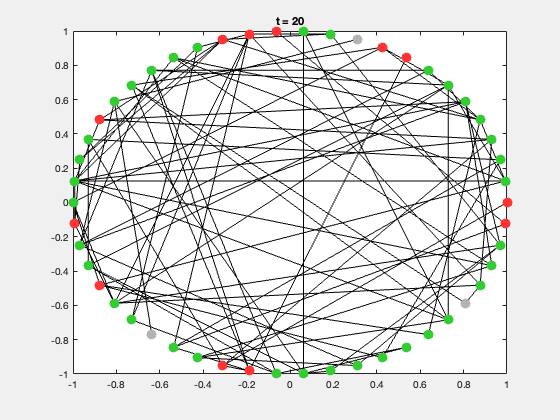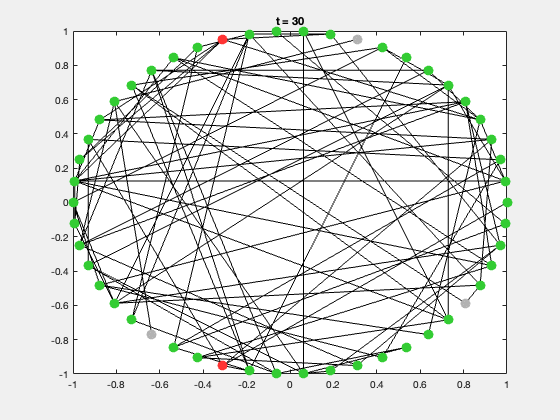
典型的研究问题包括：

传染病在社交网络中的传播；
信息在社交平台上的扩散；
电力网络或神经网络的同步；
系统中失效的传播。

抽象公式：
$xi(t+1)=f(xi(t),{xj(t)}j∈Ni)x_i(t+1) = f(x_i(t), \{x_j(t)\}_{j \in N_i})$

其中：

$x_i(t)$ ：节点 $i$ 在时刻 $t$ 的状态；
$N_i$ ：与节点 $i$ 相连的邻居集合；
$f(⋅)f(\cdot)$ ：状态更新规则。

二、SIR 传染病模型概述

SIR 模型是网络动力学中最经典的传播模型。
每个节点有三种状态：

状态	含义	颜色
S	易感者（Susceptible）	灰色
I	感染者（Infected）	红色
R	康复者（Recovered）	绿色

状态转移规则：
$\xrightarrow{\beta} 2I, \quad I \xrightarrow{\gamma} R$

感染率 $β\beta$ ：感染者以概率传播给邻居
康复率 $γ\gamma$ ：感染者以概率康复

三、Python 实现

下面是一个简单可复现的 Python 版本，用于模拟传播过程：

import networkx as nx
import random
import matplotlib.pyplot as plt# 构建网络
G = nx.erdos_renyi_graph(50, 0.05)# 初始化节点状态
state = {node: 'S' for node in G.nodes()}
state[random.choice(list(G.nodes()))] = 'I'beta = 0.3
gamma = 0.1
steps = 30# 仿真
for t in range(steps):new_state = state.copy()for node in G.nodes():if state[node] == 'I':for nbr in G.neighbors(node):if state[nbr] == 'S' and random.random() < beta:new_state[nbr] = 'I'if random.random() < gamma:new_state[node] = 'R'state = new_state.copy()# 绘图color_map = {'S': 'skyblue', 'I': 'red', 'R': 'gray'}colors = [color_map[state[n]] for n in G.nodes()]nx.draw(G, node_color=colors, with_labels=False)plt.title(f'Time step {t}')plt.pause(0.3)plt.clf()

四、MATLAB 实现（直接输出仿真图）

MATLAB 版本可以直接显示传播过程的静态图或逐步演示：

%% 复杂网络 SIR 模型仿真（MATLAB 可视化示例）
clc; clear; close all;%% 网络参数
N = 50;           % 节点数
p = 0.07;         % ER 网络连边概率
steps = 30;       % 仿真步数%% 构建随机网络（ER 网络）
G = rand(N) < p;
G = triu(G,1);    % 只保留上三角
G = G + G';       % 对称邻接矩阵%% 初始化节点状态
state = repmat("S", N, 1); % 全部初始为易感者
state(randi(N)) = "I";     % 随机选择一个感染者%% SIR 模型参数
beta = 0.3;   % 感染率
gamma = 0.1;  % 康复率%% 节点布局（圆形）
theta = linspace(0, 2*pi, N+1);
pos = [cos(theta(1:N))', sin(theta(1:N))'];%% 定义颜色映射
color_map = containers.Map(["S","I","R"], ...{[0.7 0.7 0.7], ...  % S 灰色[1 0.2 0.2], ...    % I 红色[0.2 0.8 0.2]});    % R 绿色%% 仿真循环
figure('Position',[100 100 600 600]);
for t = 1:stepsnew_state = state;% 状态更新for i = 1:Nif state(i) == "I"neighbors = find(G(i,:));for j = neighborsif state(j) == "S" && rand < betanew_state(j) = "I";endendif rand < gammanew_state(i) = "R";endendendstate = new_state;% 绘制网络clf;gplot(G, pos, 'k-');  % 绘制连边hold on;% 每个节点的颜色node_colors = zeros(N,3);for k = 1:Nnode_colors(k,:) = color_map(state(k));endscatter(pos(:,1), pos(:,2), 100, node_colors, 'filled');title(['SIR 网络仿真, t = ' num2str(t)]);axis equal;axis off;drawnow;
end