基于IMM交互式多模型卡尔曼滤波的目标位置和速度估计matlab仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.部分程序
4.算法理论概述
5.完整程序
1.程序功能描述
交互式多模型IMM算法是一种用于处理机动目标跟踪的自适应滤波方法,其核心思想是通过多个并行运行的卡尔曼滤波器(对应不同运动模型)对目标状态进行估计,再根据模型概率加权融合得到最终结果。该算法特别适用于目标运动模式存在突变的场景,通过模型间的动态切换机制提高跟踪鲁棒性。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
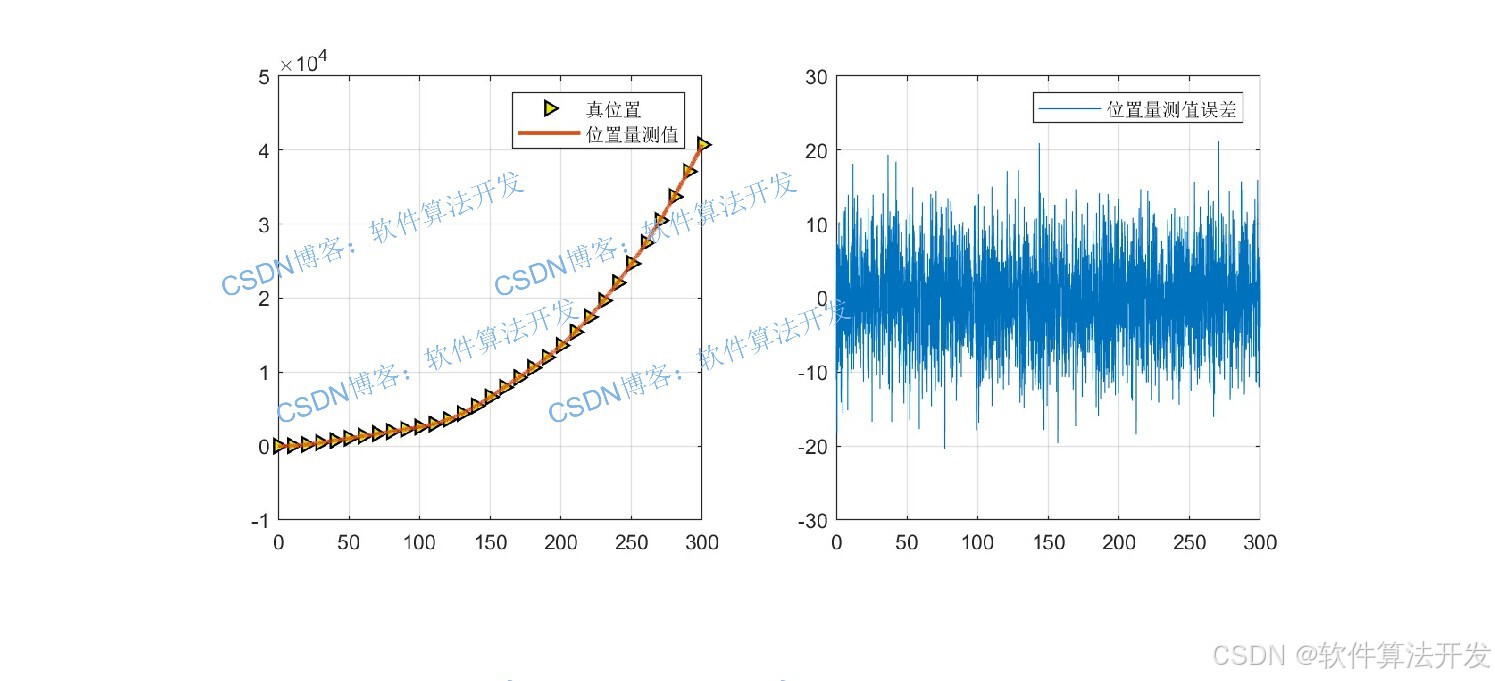
1.测量值分析:左侧对比真实位置与带噪声的测量值,右侧显示测量误差,验证了测量噪声的高斯特性。
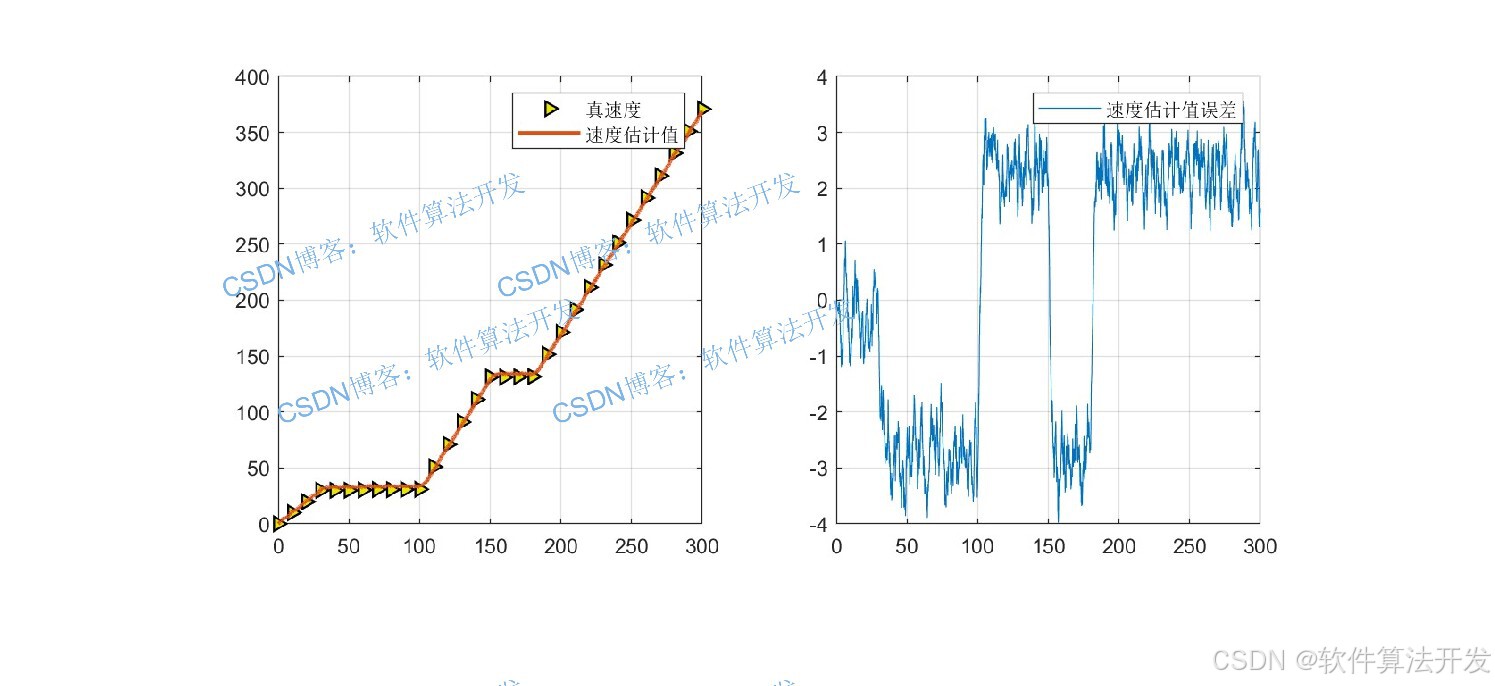
2.速度估计:左侧对比真实速度与IMM估计速度,右侧显示速度估计误差,证明算法能有效跟踪速度变化。
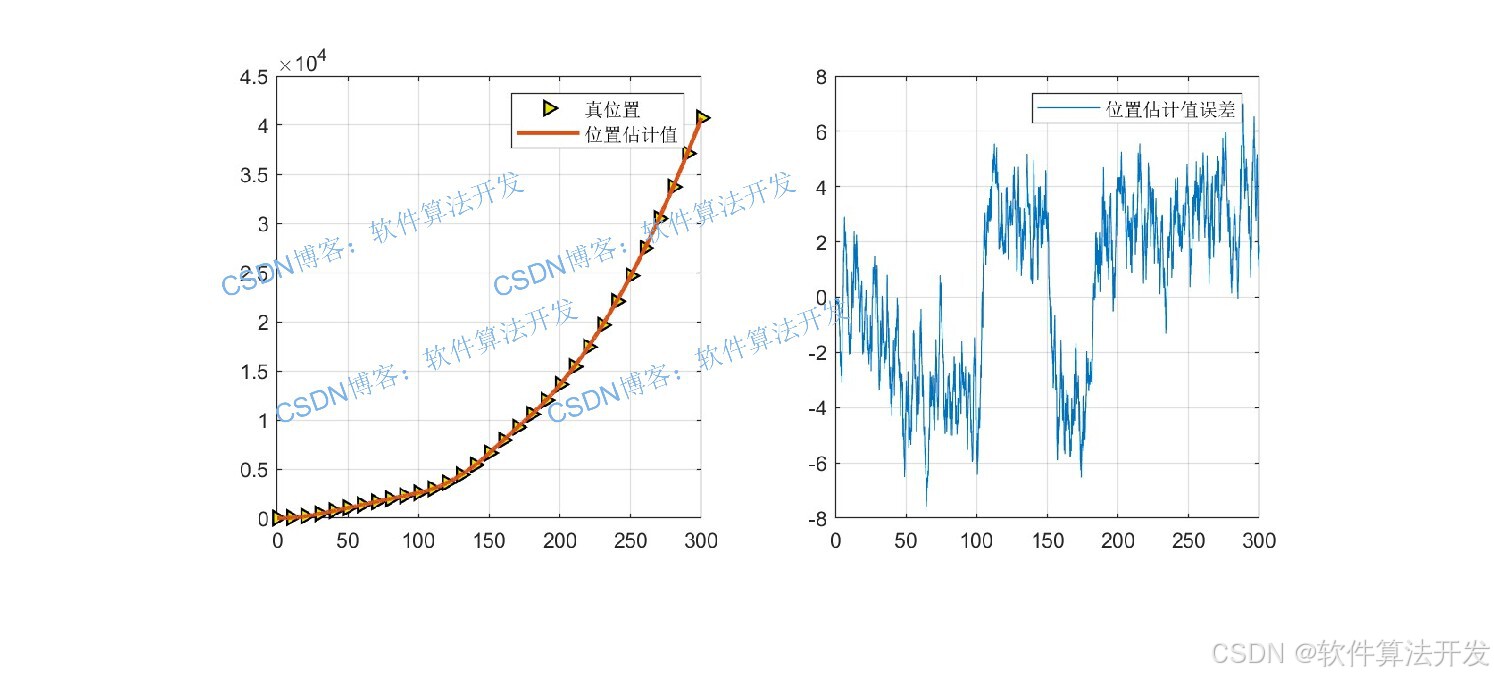
3.位置估计:左侧对比真实位置与IMM估计位置,右侧显示位置估计误差,体现了算法对机动目标的跟踪精度。 IMM算法通过模型自适应切换,在目标运动模式改变时(如30s、100s、150s、180s时刻)能快速调整,相比单一模型卡尔曼滤波具有更小的估计误差。
3.部分程序
%步长
dt = 0.1;
%持续时间
Tm = 300;
%状态转移矩阵
Amat = [1 dt;0 1];
%激励输入矩阵
Bmat = [dt^2/2;dt];
%量测矩阵
Cmat = [1 0];
%机动加速度系数矩阵
Dmat = [dt^2/2;dt];
%初始状态
Xini = [0;0];
%初始化状态估计矩阵
x_hat= [Xini Xini Xini];
%过程随机噪声方差
Q = 0.04;
%测量随机噪声方差
R = 36;
%初始化方差矩阵
1224.算法理论概述
系统采用一维运动模型,状态向量包含位置和速度:
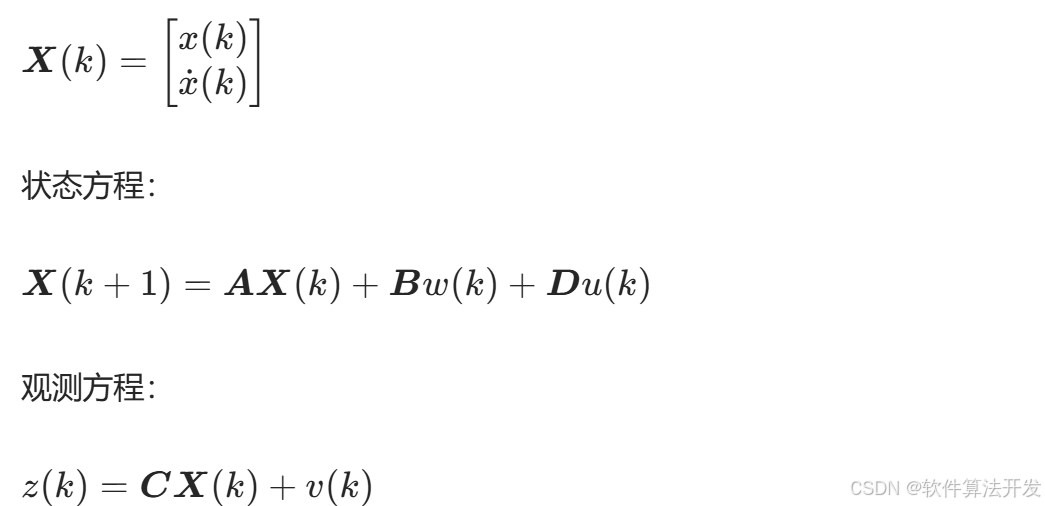

多模型设置
程序采用3个模型对应不同加速度:
模型 1: u(1)=0(匀速运动)
模型 2: u(2)=1(匀加速运动1)
模型 3: u(3)=2(匀加速运动2)
IMM核心计算流程
该阶段根据模型转移概率和先验概率,对各滤波器的初始状态进行混合,实现模型间的平滑过渡。
计算混合概率:
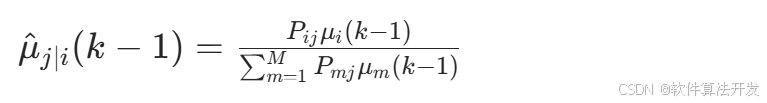
混合状态初始化:
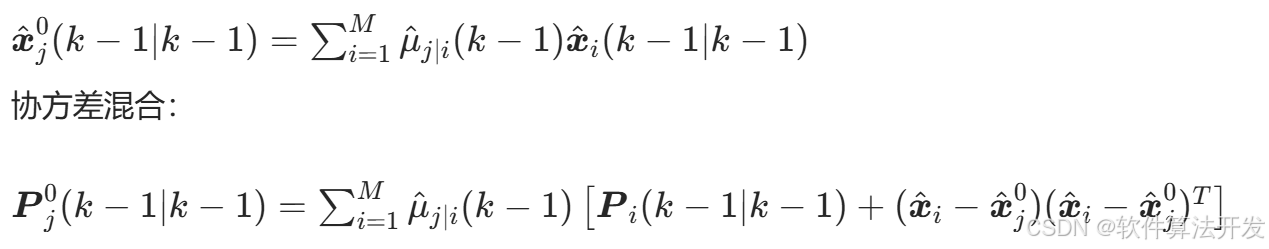
滤波阶段:
对每个模型独立运行卡尔曼滤波:
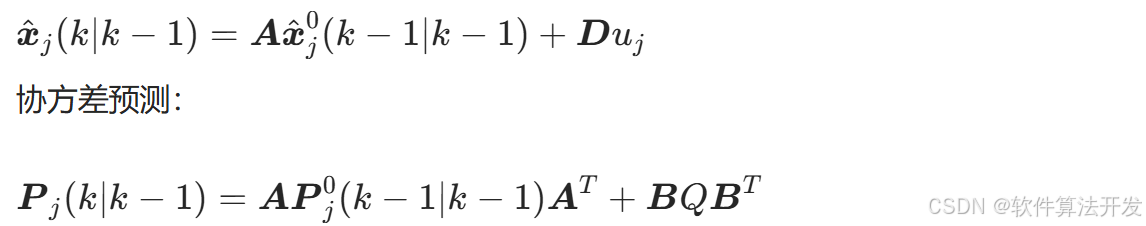
卡尔曼增益计算:
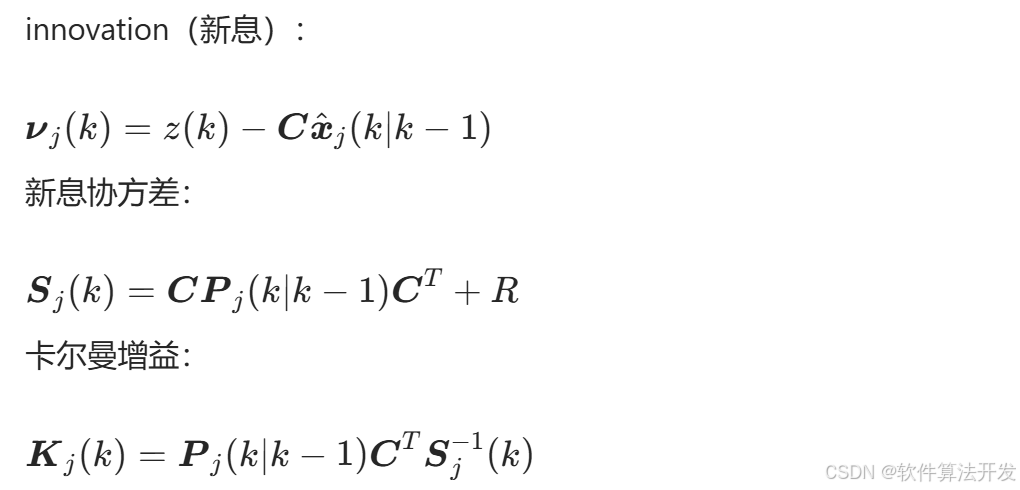
状态更新:

似然函数计算:
每个模型的似然度表示量测与模型的匹配程度:

模型概率更新:
根据似然函数更新各模型的后验概率:
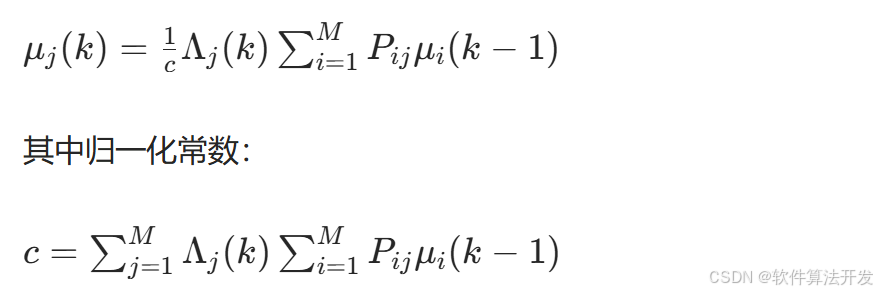
融合输出:

IMM算法通过"交互-滤波-更新-融合"四步流程,实现了对机动目标的稳健跟踪。
其核心在于: 多模型并行处理不同运动模式 模型概率动态调整权重 状态混合机制平滑模型切换 该程序完整实现了一维情况下的IMM算法,可扩展至二维 / 三维目标跟踪场景,只需相应修改状态向量和模型矩阵即可。在实际应用中,需根据目标机动特性合理设计模型集和转移概率矩阵,以获得最优跟踪性能。
5.完整程序
VVV
关注后手机上输入程序码:124
