数据结构---哈夫曼树的实现

数据结构—哈夫曼树的实现

一. 内容介绍

本次内容主要介绍的是哈夫曼树，又称最优二叉树，是一种带权路径长度最短的二叉树，主要运用于数据压缩领域。以下会介绍关于学习哈夫曼树的前置知识和专有名词概念，最后会实现哈夫曼树的搭建代码实现以及通过哈夫曼树得到哈夫曼编码的代码实现。

二. 前置知识

• 节点的路径长度：从根节点到目标节点的路径连接数（每两个节点之间的连线算一条路径）。
• 树的路径长度：树的每个叶节点的路径长度之和就是树的路径长度
• 节点的带权路径长度：节点的路径长度×节点的权值，比如节点k的权值为3，它的路径长度为2，其带权路径长度就是3×2=6.
• 树的带权路径长度（WPL）：树的所有叶⼦结点的带权路径⻓度之和。

权值可以代表一个节点（数据）的出现频率，重要性等。由此，在面对数据传输时，用二进制进行编码发送电文时怎么使电文总长度最少且不产生歧义就是根据字符出现频率利用哈夫曼编码构造一个非等长的二进制编码（WPL值越小，二叉树性能越优）。

定长编码：根据字符的数量来针对性的为每一个字符设计一个单一的编码，例如：当所需字符有两个时可以用1，0分别表示，四个字符则由00，01，10，11来表示，ASCII编码就是用8个二进制编码表示256个字符，每个字符的表示编码都是等长的。通过该方式容易出现部分字符出现频率高和一些基本不出现的情况却占用相等长度的编码造成效率不高的问题，而由哈夫曼树形成的编码则有效解决了这个问题。

三. 哈夫曼树的构造过程

1. 给出一个初始森林（W代表权值）

2. 森林中选择出两颗结点的权值最⼩的⼆叉树

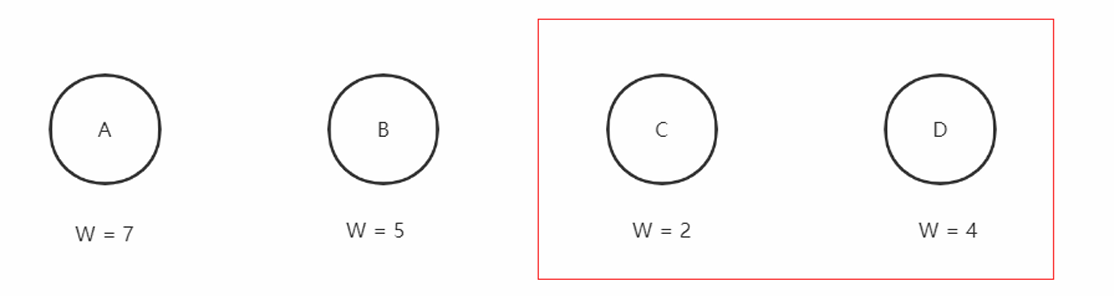
3. 合并两颗⼆叉树，增加⼀个新的结点作为新的⼆叉树的根，权值为左右孩⼦的权值之和。

   

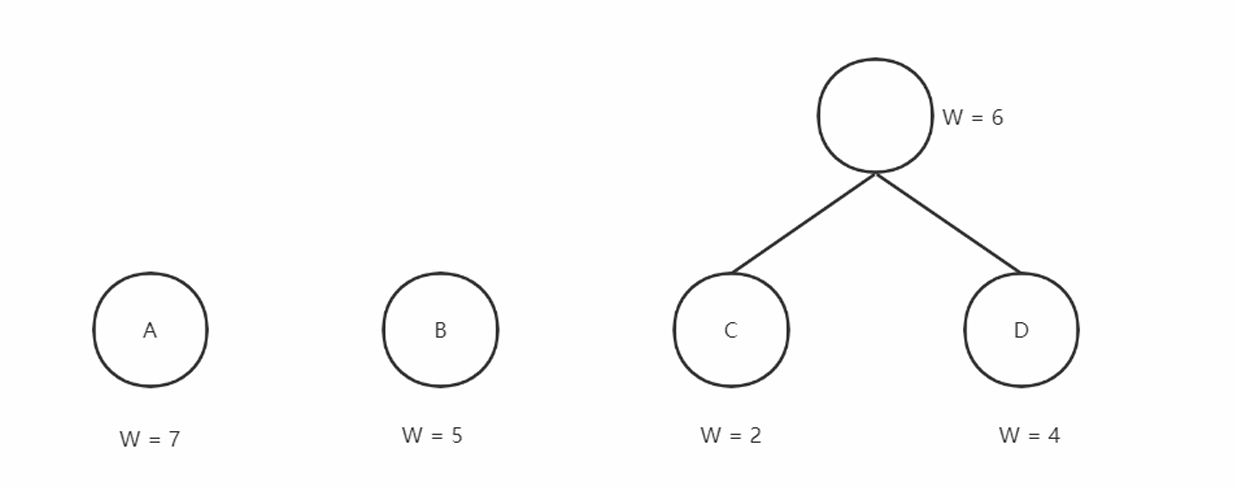
4. 不断的将新的结点跟权值最⼩的结点相结合，最终形成哈夫曼树。

四. 哈夫曼树的特征

1. 哈夫曼树是一颗二叉树

• 每片叶子节点都代表一个字符
• 从结点到其左孩⼦的路径上标记0
• 从结点到其右孩⼦的路径上标记1

2. 从根结点到包含字符的叶⼦结点的路径上获得的叶结点的编码
3. 编码均具有前缀属性

• 每⼀个叶结点不能出现在到另⼀个叶结点的路径上

• 定⻓编码可以由完整的哈夫曼树表示，并且显然具有前缀属性

五. 哈夫曼树代码实现

1. 哈夫曼树初始结构定义

// 定义Huffman树的节点结构，采用顺序存储方式，下标索引来标识不同的节点
typedef struct {int weight;int parent;int lChild;int rChild;
} HuffmanNode, *HuffmanTree;//节点与树根结构体一致，同时定义typedef char *HuffmanCode;

2. 查找权值较小的节点

哈夫曼树的实现是基于像下图这样的已知节点与权值然后注意构建成树

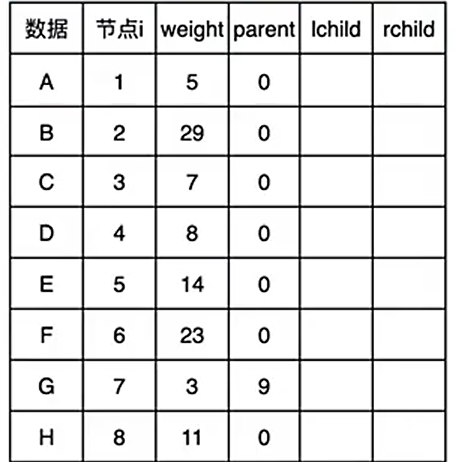
static void selectNode(HuffmanTree tree, int n, int *s1, int *s2)
{int mini = 0;for (int i = 1; i <= n; ++i){if (tree[i].parent == 0)//找到第一个父节点为0的节点{mini = i;break;}}for (int i = 1; i <= n; ++i){if (tree[i].parent == 0){if (tree[i].weight < tree[mini].weight)//查找权值最小节点的编号{mini = i;}}}*s1 = mini;//将权值最小节点编号赋值给是s1（s1为地址，会将值返回到函数外的s1）for (int i = 1; i <= n; ++i){if (tree[i].parent == 0 && i != *s1)//排除s1{mini = i;break;}}for (int i = 1; i <= n; ++i){if (tree[i].parent == 0 && i != *s1)//排除s1，寻找次大值{if (tree[i].weight < tree[mini].weight){mini = i;}}}*s2 = mini;
}

3. 搭建哈夫曼树

因为构建哈夫曼树是在已知所有节点以及其权值的情况下，节点数固定，所以运用顺序表结构来存可以充分利用空间。

HuffmanTree createHuffmanTree(const int* w, int n)
{HuffmanTree tree;int m = 2*n-1;//哈夫曼树节点数目固定为字符数n*2-1tree = malloc(sizeof(HuffmanNode) * (m+1));//申请空间（因为从编号1开始搭建，所以申请m+1个节点的空间）if (tree == NULL){return NULL;}for (int i = 1; i <= m; ++i)//逐一初始化{tree[i].parent = tree[i].lChild = tree[i].rChild = 0;tree[i].weight = 0;}for (int i = 1; i <= m; ++i)//将权值一一赋值给节点，进行初始化{tree[i].weight = w[i-1];}int s1,s2;for (int i = n + 1;i <= m;i++){selectNode(tree,i - 1,&s1,&s2);//得到权值最小和次小值tree[s1].parent = tree[s2].parent = i;//创建新节点作为得到的两个节点的根节点tree[i].lChild =s1;//权值最小作为新建节点的左子节点tree[i].rChild =s2;//权值次小作为新建节点的右子节点tree[i].weight =tree[s1].weight + tree[s2].weight;//新建节点权值为两个子节点权值之和}return tree;//将构建好的哈夫曼树返回
}

4. 生成哈夫曼编码

HuffmanCode* createHuffmanCode(HuffmanTree tree, int n)
{huafumanbianmaHuffmanCode* codes = malloc(sizeof(HuffmanCode) * n);//n个字符对应n个哈夫曼编码if (codes == NULL)//申请失败{return NULL;}memset(codes,0,sizeof(HuffmanCode) * n);//将申请的空间全初始化为0// 每求一个字符时，倒序构建，n个节点，树的高度最高是n，编码个数最多为nchar* temp = malloc(sizeof(char) * n);//定义一个temp存储每一个字符的哈夫曼编码int start;// temp空间的起始位置int p;// 存放当前节点的父节点信息int pos;// 当前编码的位置for (int i = 1; i <= n; ++i)// 逐个字符求Huffman编码{start = n - 1;temp[start] = '\0';//首先在编码末尾存入结束标识\0pos = i;p = tree[i].parent;while (p)//判断语句：父节点存在{start--;//向前编码temp[start] = (tree[p].lChild == pos) ? '0' : '1';//如果当前节点是p的左子节点，则根据左0右1生成编码pos = p;//更新编码位置p = tree[p].parent;//更新父节点}codes[i-1] = malloc(sizeof(HuffmanCode) * (n-start));//生成编码长度为n-start，生成等长空间，防止浪费strcpy(codes[i-1],&temp[start]);//将temp生成编码复制到codes的i-1位置（codes申请的为0~n-1，i的取值为1~n，所以前移一位）}free(temp);//将temp释放return codes;
}

六. 内容总结

本次哈夫曼树构建和哈夫曼编码生成的代码逻辑不难，主要在于理解哈夫曼树的作用以及这么构建生成的树的好处。简单来说就是通过每次寻找当前父节点为0权值相对最小的两个节点作为子节点创建一个新节点，不断重复此操作直到构建完成，由此生成一颗哈夫曼树。关于哈夫曼编码就是在上述哈夫曼树构建成功后，找到需要编码的字符所代表的叶子节点，从根节点开始向下搜索该节点，途径节点都按照左0右1合成一个该字符的哈夫曼编码（权值越小，该字符代表节点高度越高，生成编码越长）。总体来看就是这样，关于本节内容有问题可以在评论区问。