当前位置：首页 > news >正文

MATLAB基于PSO-GA的铁路工程施工进度计划多目标优化研究

news 2025/11/12 6:55:58

在这里插入图片描述

基于PSO-GA混合算法的铁路工程施工进度计划多目标优化研究

摘要

本研究针对铁路工程施工进度计划中工期、成本、资源均衡等多目标相互冲突的复杂优化问题，提出一种融合粒子群优化算法（PSO）和遗传算法（GA）的混合智能优化模型（PSO-GA）。该模型利用PSO强大的全局搜索能力和GA的交叉、变异操作保持种群多样性的优点，克服单一算法易陷入局部最优、早熟收敛的缺陷。通过建立以最短工期、最低成本、最佳资源均衡度为核心的多目标优化函数，并综合考虑铁路工程中的逻辑约束、资源约束、工期约束等，利用该混合算法进行求解。最后，通过一个实际或仿真的铁路工程项目案例进行验证，结果表明，PSO-GA混合算法相较于单一PSO或GA，在求解质量和收敛速度上均有显著提升，能为项目管理者的科学决策提供有效支持。

关键词：铁路工程；施工进度优化；多目标优化；粒子群算法；遗传算法；PSO-GA混合算法

1. 引言

研究背景与意义：
- 背景：铁路工程具有投资巨大、建设周期长、技术复杂、参与单位多、风险高等特点。科学合理的施工进度计划是项目成功的关键。
- 意义：传统的进度计划（如关键路径法CPM）多侧重于单一工期目标，难以平衡成本、资源等多重目标。多目标优化是实现项目精益化管理、降本增效的必然要求。
国内外研究现状：
- 简述国内外在工程项目进度优化方面的研究，包括传统数学规划方法、元启发式算法（如GA、PSO、蚁群算法等）的应用。
- 指出单一算法的局限性（如GA局部搜索能力弱、PSO易早熟），引出混合算法成为研究趋势。
- 点明将PSO-GA应用于铁路工程这一特定领域的创新性和必要性。
研究内容与技术路线：
- 明确本研究的主要内容：构建多目标优化模型、设计PSO-GA混合算法、进行案例仿真与对比分析。
- 给出研究的技术路线图。

2. 铁路工程施工进度多目标优化模型的建立

问题描述：
- 将铁路工程项目分解为具有先后逻辑关系的多个工序（WBS）。
- 每个工序有多个可选的施工方案（即不同的工期、成本、资源消耗组合）。
- 优化目标是在满足各种约束条件下，从海量方案组合中寻找非劣解集（Pareto最优解集）。
目标函数的确定：
- 目标一：工期最短（T）
  Min T = max(EFT_i)，其中EFT_i为所有工序的最早完成时间。
- 目标二：总成本最低（C）
  Min C = C_direct + C_indirect。直接成本C_direct与工期相关（通常工期缩短，直接成本增加），间接成本C_indirect随时间递增。
- 目标三：资源均衡度最佳（R）
  常用资源方差来衡量，如对于某种资源k：Min R_k = Σ (r_k(t) - ŕ_k)^2 / T，其中r_k(t)为第t天的资源用量，ŕ_k为日均用量。可以综合考虑多种关键资源（如人力、机械）。
约束条件：
- 逻辑约束：工序间的紧前紧后关系（FS、SS、FF、SF等）。
- 资源约束：任何时刻的资源使用量不超过最大可用量。
- 工期约束：总工期不超过合同要求。
- 非负与离散约束：工序工期、开始时间等为非负整数。
多目标处理：
- 采用加权和法或Pareto排序法。
- 推荐使用Pareto排序法：因为它能直接得到一个解集，供决策者根据偏好选择。通过引入非支配排序和拥挤度计算来维持解集的多样性。

3. PSO-GA混合优化算法的设计

这是本研究的核心章节。

编码设计：
- 采用基于工序的实数编码。一个粒子/染色体表示一个进度计划，其维度等于工序数，每个位置的值代表该工序的开始时间或所选方案模式。
PSO部分设计：
- 粒子位置与速度：粒子位置X_i即一个进度计划编码，速度V_i表示位置更新的方向和步长。
- 更新公式：V_i(t+1) = w * V_i(t) + c1 * r1 * (Pbest_i - X_i(t)) + c2 * r2 * (Gbest - X_i(t))
  X_i(t+1) = X_i(t) + V_i(t+1)
- 参数设置：惯性权重w（可采用线性递减策略），学习因子c1, c2，随机数r1, r2。
GA部分设计：
- 选择操作：采用轮盘赌或锦标赛选择法，适应度由Pareto等级和拥挤度共同决定。
- 交叉操作：采用两点交叉或均匀交叉，用于混合不同粒子的优良基因。
- 变异操作：采用单点变异或高斯变异，以一定概率随机改变某个工序的开始时间，增强局部搜索和跳出局部最优的能力。
PSO-GA混合策略：
- 核心思想：以PSO框架为主，定期引入GA操作来增强种群多样性。
- 混合流程：
  1. 初始化种群，计算每个个体的目标函数值。
  2. 进行非支配排序和拥挤度计算。
  3. PSO更新：根据PSO公式更新每个粒子的速度和位置。
  4. 混合判断：每隔N代，或当检测到种群多样性下降（如收敛速度过快）时，执行以下步骤：
    a. 选择：从当前种群中选择优良个体。
    b. 交叉与变异：对选出的个体执行GA的交叉和变异操作，产生新的子代。
    c. 合并：将父代种群与子代种群合并。
    d. 精英保留：对合并后的种群进行非支配排序，选择前NP个最优个体作为新一代种群。
  5. 更新个体最优Pbest和全局最优Gbest（在多目标中为外部档案集）。
  6. 判断是否满足终止条件（如最大迭代次数），若满足则输出外部档案集中的Pareto最优解集，否则返回步骤2。

4. 案例仿真与结果分析

案例背景：
- 选取一个典型的铁路工程项目（如一段隧道、一座桥梁或一个车站），列出其WBS、工序关系、各工序的工期-成本选项、资源需求等基础数据。
仿真实验：
- 设置算法参数（种群大小、迭代次数、w、c1、c2、交叉率、变异率等）。
- 分别运行标准PSO、标准GA和本文的PSO-GA混合算法。
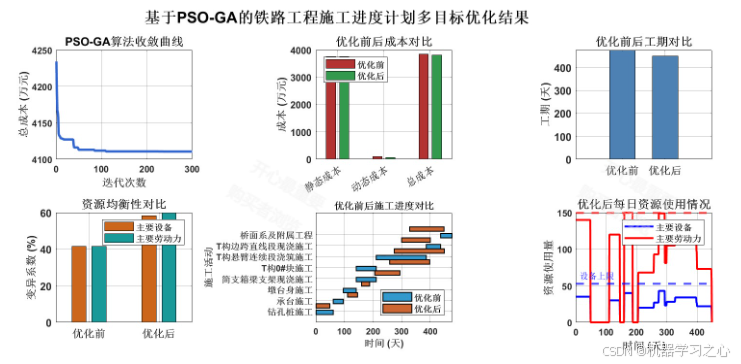
结果对比与分析：
- 收敛性对比：绘制各算法的迭代收敛曲线（如世代距离GD、反世代距离IGD等指标），展示PSO-GA更优的收敛速度和精度。
- 解集质量对比：绘制三组算法得到的Pareto前沿面，直观展示PSO-GA得到的解集在分布广度和均匀性上的优势。
- 方案决策：从PSO-GA的Pareto解集中，选取几个典型方案（如最短工期方案、最低成本方案、资源最均衡方案）进行详细分析，展示其工程实际意义。