当前位置：首页 > news >正文

电磁波传播理论的数学描述和python模拟

news 2025/11/12 6:39:39

概述

1 电磁波传播理论

1.1 麦克斯韦方程组和波动方程

1.2 理论基础：麦克斯韦方程组

1.3 电磁波的推导：从方程组到波动方程

1.4 核心数学工具与概念

1.5 传播特性的数学描述

2 系统模拟

2.1 电磁波传播模拟

2.1.1 代码实现

2.1.2 运行结果

2.2 电磁波的偏振状态

2.2.1 代码实现

2.2.2 运行结果

2.3 电磁波在介质中的传播

2.3.1 代码实现

2.3.2 运行结果

2.4 反射和折射

2.4.1 代码实现

2.4.2 运行结果

2.5 波导和谐振腔

2.5.1 代码实现

2.5.2 运行结果

2.6 天线辐射

2.6.1 代码实现

2.6.2 运行结果

概述

电磁波传播理论的数学原理深邃而优美，其核心是麦克斯韦方程组。一切电磁现象的起点都是这组由詹姆斯·克拉克·麦克斯韦在19世纪总结的四个方程。它们描述了电场 (E) 和磁场 (B) 是如何由电荷和电流产生，以及它们之间如何相互作用的。本文介绍电磁波传播的基本理论，并提供相应的Python实现。

1 电磁波传播理论

电磁波传播理论是电磁学的核心内容，描述了电磁场在空间和时间中的传播规律。

电磁波传播理论的数学原理是一个严谨而自洽的体系：

起点是描述基本实验定律的麦克斯韦方程组（矢量微积分）。
通过数学推导（取旋度、应用恒等式），在自由空间中导出波动方程（偏微分方程），预言了电磁波的存在和速度。
对于时谐场，波动方程简化为亥姆霍兹方程，便于分析空间模式。
在具体问题中，需要应用边界条件来求解。
最后，用波阻抗、坡印廷矢量和极化等数学概念来精确描述波的传播特性。

这个数学框架不仅完美地解释了光、无线电波、微波等所有电磁现象，也是现代无线通信、雷达、光学等技术领域的基石。下面具体介绍其数学原理。

1.1 麦克斯韦方程组和波动方程

1）基本方程

麦克斯韦方程组是电磁理论的基础：

∇·E = ρ/ε₀

∇·B = 0

∇×E = -∂B/∂t

∇×B = μ₀J + μ₀ε₀∂E/∂t

在真空中（ρ=0, J=0），可以得到波动方程：

∇²E - (1/c²)∂²E/∂t² = 0

∇²B - (1/c²)∂²B/∂t² = 0

其中 c = 1/√(μ₀ε₀) 是光速。

1.2 理论基础：麦克斯韦方程组

一切电磁现象的起点都是这组由詹姆斯·克拉克·麦克斯韦在19世纪总结的四个方程。它们描述了电场 (E) 和磁场 (B) 是如何由电荷和电流产生，以及它们之间如何相互作用的。

在微分形式下，它们写作：

1） 高斯定律：

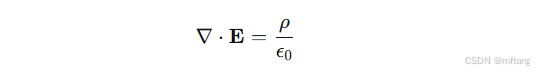
数学原理：电场的散度正比于电荷密度 ρρ。这说明电场线从正电荷发出，终止于负电荷。散度算子 (∇⋅) 衡量了场在一点上的“源”或“汇”的强度。

2） 高斯磁定律：

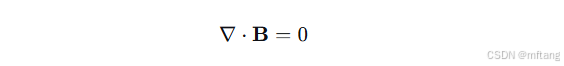
数学原理：磁场的散度处处为零。这说明不存在磁单极子，磁场线永远是闭合的环路。

3） 法拉第电磁感应定律：

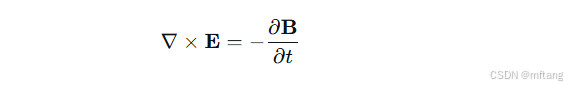
数学原理：电场的旋度正比于磁场随时间的变化率的负值。旋度算子 (∇×∇×) 衡量了场在一点上的旋转倾向。这个方程说明了变化的磁场会感生出涡旋电场（这就是发电机和变压器的原理）

4） 安培-麦克斯韦定律：

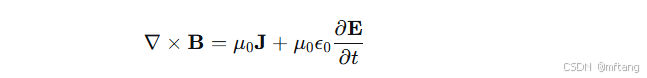
其中：

数学原理：磁场的旋度由两部分贡献：传导电流密度 JJ 和变化的电场（即“位移电流”ϵ0∂E∂tϵ0∂t∂E）。麦克斯韦添加的位移电流项是革命性的，它预言了电磁波的存在。

1.3 电磁波的推导：从方程组到波动方程

电磁波的关键思想是：变化的电场产生变化的磁场，变化的磁场又产生变化的电场，如此循环，能量就可以在空间中传播，形成波。

我们从麦克斯韦方程组出发，在自由空间（没有自由电荷和电流，即 ρ=0,J=0）中进行推导。

1） 对法拉第定律取旋度：

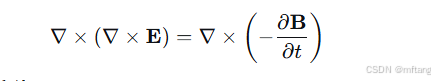
2） 应用矢量恒等式并代入安培定律：

3） 得到电场的波动方程：

将左右两边相等：

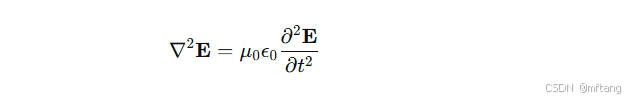
这是一个标准的三维波动方程！

4） 同样，对安培定律取旋度可以得到磁场的波动方程：

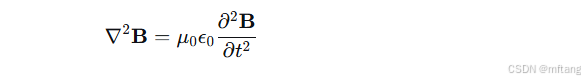
数学原理分析：

1.4 核心数学工具与概念

1） 矢量微积分

散度 (∇⋅)：衡量源的强度。高斯定律用它来描述场与源的关系。

旋度 (∇×)：衡量场的旋转性。法拉第定律和安培定律用它来描述电场和磁场的相互激发。

这些算子将全局的积分定律（如环路积分、曲面积分）转化为强大的局部微分形式，是推导波动方程的基础。

2） 偏微分方程

麦克斯韦方程组本身就是一个耦合的偏微分方程组。

波动方程是经典的二阶线性齐次偏微分方程。其解描述了波的传播行为。

3） 时谐场的复数表示与亥姆霍兹方程

对于单一频率 ω的电磁波（时谐场），我们可以假设场的形式为：

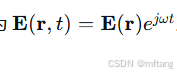
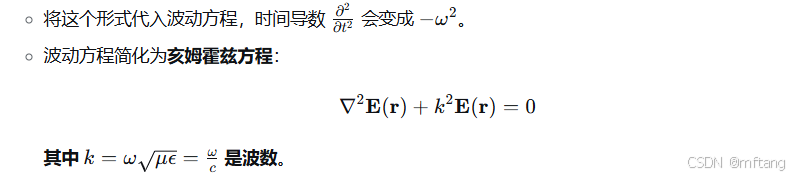
数学原理：亥姆霍兹方程将时间变量分离出去，使我们能专注于研究电磁波在空间中的分布（模式），这对于分析波导、谐振腔和天线辐射问题至关重要。

4） 边界条件

当电磁波遇到不同介质的分界面时，麦克斯韦方程组积分形式导出了边界条件：

电场的切向分量连续。

磁场的切向分量可能存在跳跃（如果存在表面电流）。

电位移矢量 D 的法向分量存在跳跃（如果存在面电荷）。

磁感应强度 B 的法向分量连续。

数学原理：这些边界条件是求解具体场景下电磁波传播（如反射、折射）的关键约束条件。

1.5 传播特性的数学描述

1) 波阻抗：

在自由空间中，电场与磁场的幅度之比是一个常数，称为本征阻抗：

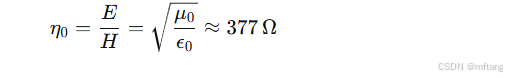
这描述了电磁波中电、磁能量携带的“搭配”关系。

2) 坡印廷矢量：

描述了电磁能流的瞬时功率密度和方向。

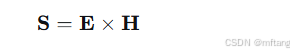
数学原理：这是一个矢量叉乘，其方向代表了能量流动的方向（垂直于E和H所在的平面），大小代表了功率流密度。它定量地描述了电磁波如何携带和传输能量。

3) 极化：

由电场矢量末端点在空间固定位置随时间划出的轨迹定义。

2 系统模拟

2.1 电磁波传播模拟

麦克斯韦方程组描述电磁场基本规律

波动方程描述电磁波传播

平面波解是最基本的传播形式

2.1.1 代码实现

import matplotlib
import matplotlib.pyplot as plt
from scipy.integrate import odeintmatplotlib.use('TkAgg')# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签（黑体）
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号import numpy as np
import matplotlib.pyplot as pltimport numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from scipy import constants
import mathclass ElectromagneticWave:"""电磁波传播模拟"""def __init__(self, frequency=1e9, amplitude=1.0, direction='z'):"""初始化电磁波参数frequency: 频率 (Hz)amplitude: 电场振幅 (V/m)direction: 传播方向"""self.f = frequencyself.E0 = amplitudeself.direction = direction# 物理常数self.c = constants.c  # 光速self.mu0 = constants.mu_0  # 真空磁导率self.epsilon0 = constants.epsilon_0  # 真空介电常数# 波参数self.wavelength = self.c / self.fself.k = 2 * np.pi / self.wavelength  # 波数self.omega = 2 * np.pi * self.f  # 角频率print(f"电磁波参数:")print(f"频率: {self.f / 1e6:.1f} MHz")print(f"波长: {self.wavelength:.3f} m")print(f"波数: {self.k:.3f} rad/m")print(f"角频率: {self.omega / 1e6:.1f} Mrad/s")print(f"光速: {self.c:.1f} m/s")def plane_wave_field(self, x, y, z, t, polarization='x'):"""计算平面波的电磁场polarization: 偏振方向 ('x' 或 'y')"""# 传播方向if self.direction == 'z':k_dot_r = self.k * zelif self.direction == 'x':k_dot_r = self.k * xelse:  # 'y'k_dot_r = self.k * yphase = k_dot_r - self.omega * t# 电场E = np.zeros(3)if polarization == 'x':E[0] = self.E0 * np.cos(phase)  # Exelse:  # 'y'E[1] = self.E0 * np.cos(phase)  # Ey# 磁场 (与电场垂直，振幅关系 B0 = E0/c)B = np.zeros(3)if polarization == 'x' and self.direction == 'z':B[1] = (self.E0 / self.c) * np.cos(phase)  # Byelif polarization == 'y' and self.direction == 'z':B[0] = -(self.E0 / self.c) * np.cos(phase)  # Bxreturn E, Bdef spherical_wave_field(self, x, y, z, t, source_pos=[0, 0, 0], polarization='radial'):"""计算球面波的电磁场"""# 计算距离r = np.sqrt((x - source_pos[0]) ** 2 +(y - source_pos[1]) ** 2 +(z - source_pos[2]) ** 2)# 避免除零r = np.maximum(r, 1e-10)phase = self.k * r - self.omega * t# 球面波振幅衰减amplitude = self.E0 / r# 电场 (径向偏振)E = np.zeros(3)if polarization == 'radial':# 径向单位向量r_vec = np.array([x - source_pos[0],y - source_pos[1],z - source_pos[2]]) / rE = amplitude * np.cos(phase) * r_vec# 磁场 (与电场垂直)B = np.zeros(3)# 简化计算，方向近似垂直于传播方向return E, Bdef basic_em_wave_visualization():"""基本电磁波可视化"""# 创建电磁波em_wave = ElectromagneticWave(frequency=100e6, amplitude=1.0)  # 100 MHz# 空间网格z = np.linspace(0, 3 * em_wave.wavelength, 200)t_values = np.linspace(0, 2 * np.pi / em_wave.omega, 8)  # 一个周期内的时间# 计算场值E_fields = []B_fields = []for t in t_values:E_z = []B_z = []for zi in z:E, B = em_wave.plane_wave_field(0, 0, zi, t, polarization='x')E_z.append(E[0])  # Ex分量B_z.append(B[1])  # By分量E_fields.append(E_z)B_fields.append(B_z)# 绘制电磁波传播fig, axes = plt.subplots(2, 2, figsize=(12, 8))# 电场和磁场随时间变化colors = plt.cm.viridis(np.linspace(0, 1, len(t_values)))for i, t in enumerate(t_values):axes[0, 0].plot(z, E_fields[i], color=colors[i],linewidth=2, alpha=0.7, label=f't={t * 1e9:.1f}ns')axes[0, 1].plot(z, B_fields[i], color=colors[i],linewidth=2, alpha=0.7, label=f't={t * 1e9:.1f}ns')axes[0, 0].set_xlabel('位置 z (m)')axes[0, 0].set_ylabel('电场 Ex (V/m)')axes[0, 0].set_title('电场传播')axes[0, 0].grid(True, alpha=0.3)axes[0, 1].set_xlabel('位置 z (m)')axes[0, 1].set_ylabel('磁场 By (T)')axes[0, 1].set_title('磁场传播')axes[0, 1].grid(True, alpha=0.3)# 时空图Z, T = np.meshgrid(z, t_values)E_matrix = np.array(E_fields)B_matrix = np.array(B_fields)im1 = axes[1, 0].contourf(Z, T * 1e9, E_matrix, levels=50, cmap='RdBu')axes[1, 0].set_xlabel('位置 z (m)')axes[1, 0].set_ylabel('时间 t (ns)')axes[1, 0].set_title('电场时空图')plt.colorbar(im1, ax=axes[1, 0], label='Ex (V/m)')im2 = axes[1, 1].contourf(Z, T * 1e9, B_matrix, levels=50, cmap='RdBu')axes[1, 1].set_xlabel('位置 z (m)')axes[1, 1].set_ylabel('时间 t (ns)')axes[1, 1].set_title('磁场时空图')plt.colorbar(im2, ax=axes[1, 1], label='By (T)')plt.tight_layout()plt.show()# 能量密度计算print("\n电磁波能量分析:")energy_density_electric = 0.5 * constants.epsilon_0 * np.array(E_fields) ** 2energy_density_magnetic = 0.5 * constants.mu_0 * np.array(B_fields) ** 2total_energy_density = energy_density_electric + energy_density_magnetic# 坡印廷矢量 (能流密度)poynting_vector = np.array(E_fields) * np.array(B_fields) / constants.mu_0plt.figure(figsize=(10, 6))plt.plot(z, energy_density_electric[0], 'r-', label='电场能量密度', linewidth=2)plt.plot(z, energy_density_magnetic[0], 'b-', label='磁场能量密度', linewidth=2)plt.plot(z, total_energy_density[0], 'k-', label='总能量密度', linewidth=2)plt.plot(z, poynting_vector[0], 'g-', label='坡印廷矢量', linewidth=2)plt.xlabel('位置 z (m)')plt.ylabel('能量密度 (J/m³) / 能流 (W/m²)')plt.title('电磁波能量分布')plt.legend()plt.grid(True, alpha=0.3)plt.show()return em_wave, E_fields, B_fields# 运行基本电磁波可视化
em_wave, E_fields, B_fields = basic_em_wave_visualization()

2.1.2 运行结果

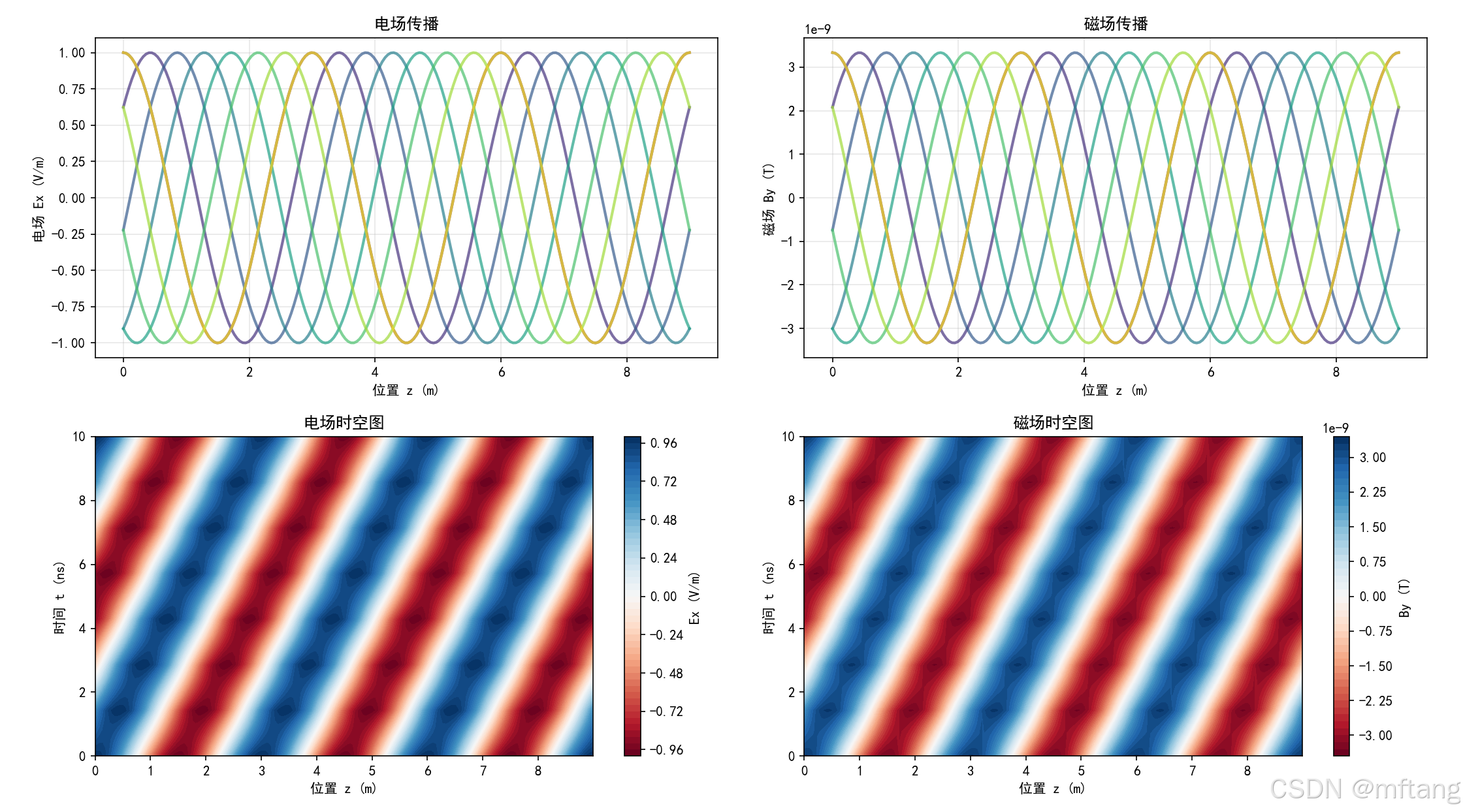
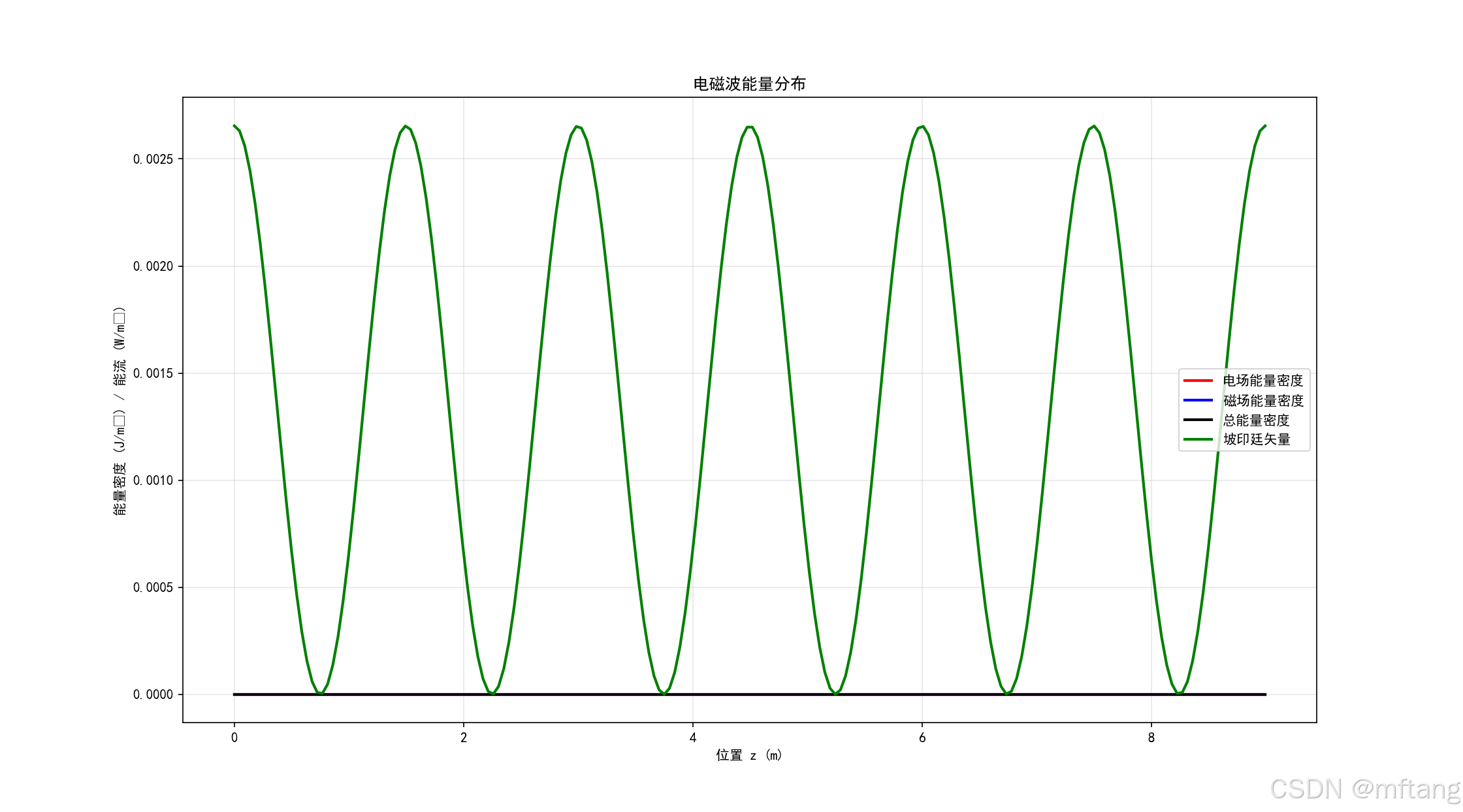
输出log：

电磁波参数:
频率: 100.0 MHz
波长: 2.998 m
波数: 2.096 rad/m
角频率: 628.3 Mrad/s
光速: 299792458.0 m/s

2.2 电磁波的偏振状态

线偏振：电场矢量在固定方向振动

圆偏振：电场矢量端点做圆周运动

椭圆偏振：最一般的偏振状态

2.2.1 代码实现

def polarization_states():"""电磁波的偏振状态"""em_wave = ElectromagneticWave(frequency=1e9, amplitude=1.0)# 时间数组t = np.linspace(0, 2 * np.pi / em_wave.omega, 100)z = 0  # 固定位置# 不同的偏振状态polarization_cases = [{'name': '线偏振 (x方向)', 'Ex_phase': 0, 'Ey_phase': 0, 'Ey_amp': 0},{'name': '线偏振 (y方向)', 'Ex_phase': 0, 'Ey_phase': 0, 'Ey_amp': 1, 'Ex_amp': 0},{'name': '线偏振 (45°)', 'Ex_phase': 0, 'Ey_phase': 0, 'Ey_amp': 1, 'Ex_amp': 1},{'name': '圆偏振 (右旋)', 'Ex_phase': 0, 'Ey_phase': -np.pi / 2, 'Ey_amp': 1, 'Ex_amp': 1},{'name': '圆偏振 (左旋)', 'Ex_phase': 0, 'Ey_phase': np.pi / 2, 'Ey_amp': 1, 'Ex_amp': 1},{'name': '椭圆偏振', 'Ex_phase': 0, 'Ey_phase': np.pi / 4, 'Ey_amp': 0.7, 'Ex_amp': 1}]fig, axes = plt.subplots(2, 3, figsize=(15, 10))axes = axes.flatten()for i, case in enumerate(polarization_cases):# 计算电场分量Ex_amp = case.get('Ex_amp', 1)Ey_amp = case.get('Ey_amp', 1)Ex_phase = case.get('Ex_phase', 0)Ey_phase = case.get('Ey_phase', 0)Ex = Ex_amp * em_wave.E0 * np.cos(em_wave.k * z - em_wave.omega * t + Ex_phase)Ey = Ey_amp * em_wave.E0 * np.cos(em_wave.k * z - em_wave.omega * t + Ey_phase)# 时间序列axes[i].plot(t * 1e9, Ex, 'r-', linewidth=2, label='Ex', alpha=0.8)axes[i].plot(t * 1e9, Ey, 'b-', linewidth=2, label='Ey', alpha=0.8)axes[i].set_xlabel('时间 (ns)')axes[i].set_ylabel('电场 (V/m)')axes[i].set_title(case['name'])axes[i].legend()axes[i].grid(True, alpha=0.3)plt.tight_layout()plt.show()# 偏振轨迹fig, axes = plt.subplots(2, 3, figsize=(15, 10))axes = axes.flatten()for i, case in enumerate(polarization_cases):# 计算电场分量Ex_amp = case.get('Ex_amp', 1)Ey_amp = case.get('Ey_amp', 1)Ex_phase = case.get('Ex_phase', 0)Ey_phase = case.get('Ey_phase', 0)Ex = Ex_amp * em_wave.E0 * np.cos(em_wave.k * z - em_wave.omega * t + Ex_phase)Ey = Ey_amp * em_wave.E0 * np.cos(em_wave.k * z - em_wave.omega * t + Ey_phase)# 偏振轨迹axes[i].plot(Ex, Ey, 'purple', linewidth=2)axes[i].set_xlabel('Ex (V/m)')axes[i].set_ylabel('Ey (V/m)')axes[i].set_title(f"{case['name']} - 偏振轨迹")axes[i].grid(True, alpha=0.3)axes[i].set_aspect('equal')# 标记起点axes[i].plot(Ex[0], Ey[0], 'ro', markersize=8)plt.tight_layout()plt.show()# 斯托克斯参数分析def stokes_parameters(Ex, Ey, phase_diff):"""计算斯托克斯参数"""I = Ex ** 2 + Ey ** 2  # 总强度Q = Ex ** 2 - Ey ** 2  # 线偏振程度U = 2 * Ex * Ey * np.cos(phase_diff)  # 45°线偏振V = 2 * Ex * Ey * np.sin(phase_diff)  # 圆偏振return I, Q, U, Vprint("斯托克斯参数分析:")for case in polarization_cases:Ex_amp = case.get('Ex_amp', 1)Ey_amp = case.get('Ey_amp', 1)phase_diff = case.get('Ey_phase', 0) - case.get('Ex_phase', 0)I, Q, U, V = stokes_parameters(Ex_amp, Ey_amp, phase_diff)print(f"{case['name']}:")print(f"  I={I:.2f}, Q={Q:.2f}, U={U:.2f}, V={V:.2f}")print(f"  偏振度: {np.sqrt(Q ** 2 + U ** 2 + V ** 2) / I:.2f}")return polarization_cases# 运行偏振状态分析
polarization_cases = polarization_states()

2.2.2 运行结果

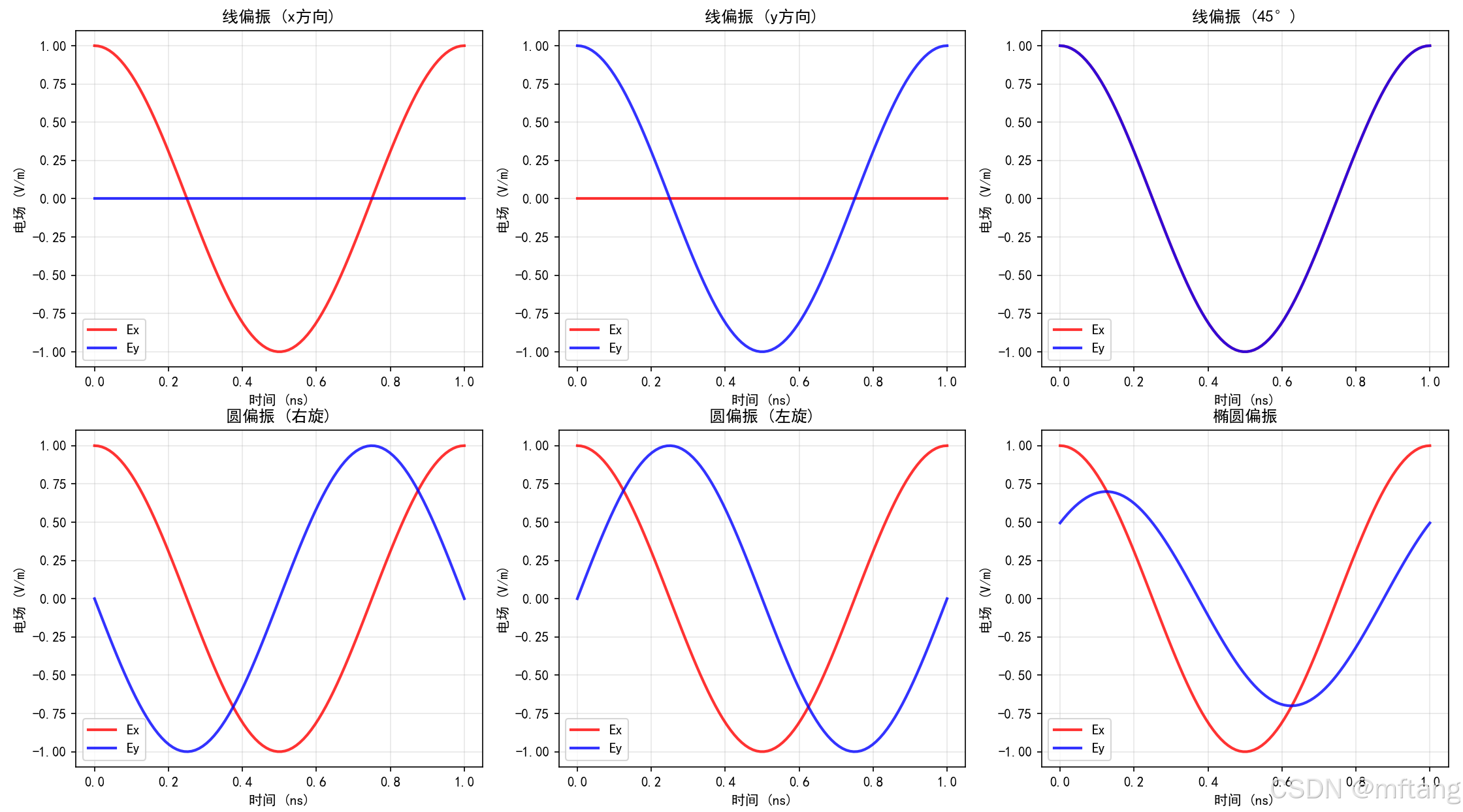
输出log：

电磁波参数:
频率: 1000.0 MHz
波长: 0.300 m
波数: 20.958 rad/m
角频率: 6283.2 Mrad/s
光速: 299792458.0 m/s

2.3 电磁波在介质中的传播

折射率影响波速和波长

导电介质引起衰减

色散现象：不同频率传播速度不同

2.3.1 代码实现

def wave_propagation_in_media():"""电磁波在介质中的传播"""class EMWaveInMedium:def __init__(self, frequency=1e9, E0=1.0, epsilon_r=1.0, mu_r=1.0, sigma=0):self.f = frequencyself.E0 = E0self.epsilon_r = epsilon_r  # 相对介电常数self.mu_r = mu_r          # 相对磁导率self.sigma = sigma        # 电导率# 物理常数self.epsilon0 = constants.epsilon_0self.mu0 = constants.mu_0# 介质参数self.epsilon = epsilon_r * self.epsilon0self.mu = mu_r * self.mu0# 复介电常数（对于导电介质）self.epsilon_complex = self.epsilon - 1j * self.sigma / (2 * np.pi * self.f)# 波参数self.k_complex = 2 * np.pi * self.f * np.sqrt(self.mu * self.epsilon_complex)self.alpha = np.real(self.k_complex)  # 衰减常数self.beta = np.imag(self.k_complex)   # 相位常数self.wavelength = 2 * np.pi / self.alpha if self.alpha > 0 else float('inf')self.phase_velocity = 2 * np.pi * self.f / self.alpha if self.alpha > 0 else float('inf')# 特征阻抗self.Z_complex = np.sqrt(self.mu / self.epsilon_complex)print(f"介质中电磁波参数:")print(f"相对介电常数: ε_r = {epsilon_r}")print(f"相对磁导率: μ_r = {mu_r}")print(f"电导率: σ = {sigma} S/m")print(f"复波数: k = {self.k_complex:.3f}")print(f"衰减常数: α = {self.alpha:.3f} Np/m")print(f"相位常数: β = {self.beta:.3f} rad/m")print(f"波长: λ = {self.wavelength:.3f} m")print(f"相速度: v_p = {self.phase_velocity/1e6:.1f} × 10⁶ m/s")print(f"特征阻抗: Z = {self.Z_complex:.3f} Ω")def field_in_medium(self, z, t):"""介质中的电磁场"""# 电场E = self.E0 * np.exp(-self.alpha * z) * np.cos(self.beta * z - 2 * np.pi * self.f * t)# 磁场H = (self.E0 / np.abs(self.Z_complex)) * np.exp(-self.alpha * z) * np.cos(self.beta * z - 2 * np.pi * self.f * t - np.angle(self.Z_complex))return E, Hdef skin_depth(self):"""趋肤深度（对于良导体）"""if self.sigma > 0:delta = 1 / np.sqrt(np.pi * self.f * self.mu * self.sigma)return deltaelse:return float('inf')# 不同介质的比较media_cases = [{'name': '真空', 'epsilon_r': 1.0, 'mu_r': 1.0, 'sigma': 0},{'name': '空气', 'epsilon_r': 1.0006, 'mu_r': 1.0, 'sigma': 0},{'name': '纯水', 'epsilon_r': 80.0, 'mu_r': 1.0, 'sigma': 0.01},{'name': '海水', 'epsilon_r': 80.0, 'mu_r': 1.0, 'sigma': 4.0},{'name': '铜', 'epsilon_r': 1.0, 'mu_r': 1.0, 'sigma': 5.8e7},{'name': '铁氧体', 'epsilon_r': 10.0, 'mu_r': 1000.0, 'sigma': 0.01}]# 空间网格z = np.linspace(0, 2, 500)  # 2米范围fig, axes = plt.subplots(2, 2, figsize=(12, 8))for i, medium in enumerate(media_cases):wave = EMWaveInMedium(frequency=1e9, E0=1.0, epsilon_r=medium['epsilon_r'], mu_r=medium['mu_r'], sigma=medium['sigma'])# 计算电场E, H = wave.field_in_medium(z, t=0)# 电场衰减axes[0, 0].semilogy(z, np.abs(E), linewidth=2, label=medium['name'])# 趋肤深度标记if medium['sigma'] > 1:delta = wave.skin_depth()axes[0, 0].axvline(x=delta, color='gray', linestyle='--', alpha=0.5)print(f"{medium['name']} 趋肤深度: {delta*100:.2f} cm")axes[0, 0].set_xlabel('深度 z (m)')axes[0, 0].set_ylabel('|E| (V/m)')axes[0, 0].set_title('不同介质中的电场衰减')axes[0, 0].legend()axes[0, 0].grid(True, alpha=0.3)# 相速度比较frequencies = np.logspace(6, 12, 100)  # 1 MHz 到 1 THzfor medium in [m for m in media_cases if m['sigma'] < 1]:  # 低损耗介质v_phase = []for f in frequencies:wave = EMWaveInMedium(frequency=f, E0=1.0,epsilon_r=medium['epsilon_r'],mu_r=medium['mu_r'],sigma=medium['sigma'])v_phase.append(wave.phase_velocity)axes[0, 1].loglog(frequencies, v_phase, linewidth=2, label=medium['name'])axes[0, 1].axhline(y=constants.c, color='k', linestyle='--', label='真空光速')axes[0, 1].set_xlabel('频率 (Hz)')axes[0, 1].set_ylabel('相速度 (m/s)')axes[0, 1].set_title('相速度随频率变化')axes[0, 1].legend()axes[0, 1].grid(True, alpha=0.3)# 波长比较for medium in [m for m in media_cases if m['sigma'] < 1]:  # 低损耗介质wavelengths = []for f in frequencies:wave = EMWaveInMedium(frequency=f, E0=1.0,epsilon_r=medium['epsilon_r'],mu_r=medium['mu_r'],sigma=medium['sigma'])wavelengths.append(wave.wavelength)axes[1, 0].loglog(frequencies, wavelengths, linewidth=2, label=medium['name'])wavelengths_vacuum = constants.c / frequenciesaxes[1, 0].loglog(frequencies, wavelengths_vacuum, 'k--', label='真空')axes[1, 0].set_xlabel('频率 (Hz)')axes[1, 0].set_ylabel('波长 (m)')axes[1, 0].set_title('波长随频率变化')axes[1, 0].legend()axes[1, 0].grid(True, alpha=0.3)# 特征阻抗比较for medium in media_cases:if medium['sigma'] < 1:  # 低损耗介质Z_values = []for f in frequencies[:10]:  # 只计算部分频率点wave = EMWaveInMedium(frequency=f, E0=1.0,epsilon_r=medium['epsilon_r'],mu_r=medium['mu_r'],sigma=medium['sigma'])Z_values.append(np.abs(wave.Z_complex))axes[1, 1].semilogy(frequencies[:10], Z_values, 'o-', linewidth=2, label=medium['name'])Z_vacuum = np.sqrt(constants.mu_0 / constants.epsilon_0)axes[1, 1].axhline(y=Z_vacuum, color='k', linestyle='--', label='真空阻抗')axes[1, 1].set_xlabel('频率 (Hz)')axes[1, 1].set_ylabel('|Z| (Ω)')axes[1, 1].set_title('特征阻抗')axes[1, 1].legend()axes[1, 1].grid(True, alpha=0.3)plt.tight_layout()plt.show()return media_cases# 运行介质中传播分析
media_cases = wave_propagation_in_media()

2.3.2 运行结果

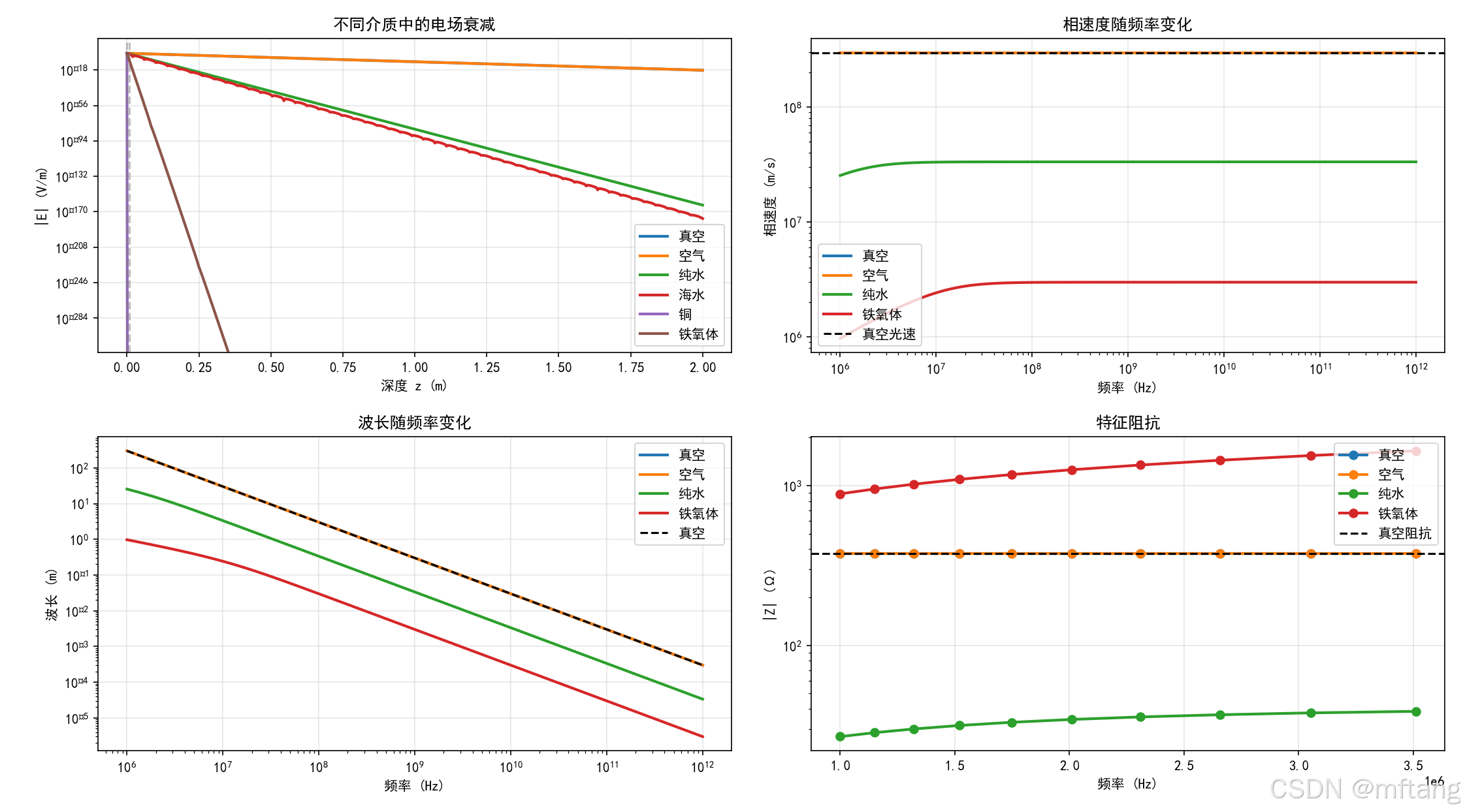
输出log：

介质中电磁波参数:
相对介电常数: ε_r = 1.0
相对磁导率: μ_r = 1.0
电导率: σ = 0 S/m
复波数: k = 20.958+0.000j
衰减常数: α = 20.958 Np/m
相位常数: β = 0.000 rad/m
波长: λ = 0.300 m
相速度: v_p = 299.8 × 10⁶ m/s
特征阻抗: Z = 376.730+0.000j Ω
介质中电磁波参数:
相对介电常数: ε_r = 1.0006
相对磁导率: μ_r = 1.0
电导率: σ = 0 S/m
复波数: k = 20.965+0.000j
衰减常数: α = 20.965 Np/m
相位常数: β = 0.000 rad/m
波长: λ = 0.300 m
相速度: v_p = 299.7 × 10⁶ m/s
特征阻抗: Z = 376.617+0.000j Ω
介质中电磁波参数:
相对介电常数: ε_r = 80.0
相对磁导率: μ_r = 1.0
电导率: σ = 0.01 S/m
复波数: k = 187.458-0.211j
衰减常数: α = 187.458 Np/m
相位常数: β = -0.211 rad/m
波长: λ = 0.034 m
相速度: v_p = 33.5 × 10⁶ m/s
特征阻抗: Z = 42.120+0.047j Ω
介质中电磁波参数:
相对介电常数: ε_r = 80.0
相对磁导率: μ_r = 1.0
电导率: σ = 4.0 S/m
复波数: k = 202.963-77.804j
衰减常数: α = 202.963 Np/m
相位常数: β = -77.804 rad/m
波长: λ = 0.031 m
相速度: v_p = 31.0 × 10⁶ m/s
特征阻抗: Z = 33.918+13.002j Ω
海水 趋肤深度: 0.80 cm
介质中电磁波参数:
相对介电常数: ε_r = 1.0
相对磁导率: μ_r = 1.0
电导率: σ = 58000000.0 S/m
复波数: k = 478513.137-478513.137j
衰减常数: α = 478513.137 Np/m
相位常数: β = -478513.137 rad/m
波长: λ = 0.000 m
相速度: v_p = 0.0 × 10⁶ m/s
特征阻抗: Z = 0.008+0.008j Ω
铜 趋肤深度: 0.00 cm
介质中电磁波参数:
相对介电常数: ε_r = 10.0
相对磁导率: μ_r = 1000.0
电导率: σ = 0.01 S/m
复波数: k = 2095.930-18.836j
衰减常数: α = 2095.930 Np/m
相位常数: β = -18.836 rad/m
波长: λ = 0.003 m

2.4 反射和折射

反射和折射遵循菲涅耳公式

布儒斯特角：反射光完全线偏振

全反射和倏逝波

2.4.1 代码实现

def reflection_refraction():"""电磁波的反射和折射"""def fresnel_coefficients(n1, n2, theta_i, polarization='TE'):"""菲涅耳系数计算n1, n2: 折射率theta_i: 入射角 (弧度)polarization: 'TE' (s偏振) 或 'TM' (p偏振)"""# 斯涅尔定律theta_t = np.arcsin(n1 * np.sin(theta_i) / n2) if n1 * np.sin(theta_i) / n2 <= 1 else np.pi/2if polarization == 'TE':# s偏振r = (n1 * np.cos(theta_i) - n2 * np.cos(theta_t)) / (n1 * np.cos(theta_i) + n2 * np.cos(theta_t))t = (2 * n1 * np.cos(theta_i)) / (n1 * np.cos(theta_i) + n2 * np.cos(theta_t))else:# p偏振r = (n2 * np.cos(theta_i) - n1 * np.cos(theta_t)) / (n2 * np.cos(theta_i) + n1 * np.cos(theta_t))t = (2 * n1 * np.cos(theta_i)) / (n2 * np.cos(theta_i) + n1 * np.cos(theta_t))return r, t, theta_tdef reflectance_transmittance(r, t, n1, n2, theta_i, theta_t, polarization='TE'):"""反射率和透射率"""R = np.abs(r)**2if polarization == 'TE':T = (n2 * np.cos(theta_t) / (n1 * np.cos(theta_i))) * np.abs(t)**2else:T = (n2 * np.cos(theta_t) / (n1 * np.cos(theta_i))) * np.abs(t)**2return R, T# 不同介质界面的反射折射interfaces = [{'name': '空气-玻璃', 'n1': 1.0, 'n2': 1.5},{'name': '玻璃-空气', 'n1': 1.5, 'n2': 1.0},{'name': '空气-水', 'n1': 1.0, 'n2': 1.33},{'name': '水-空气', 'n1': 1.33, 'n2': 1.0}]# 入射角范围theta_i_deg = np.linspace(0, 90, 100)theta_i_rad = np.radians(theta_i_deg)fig, axes = plt.subplots(2, 2, figsize=(12, 8))for i, interface in enumerate(interfaces):n1, n2 = interface['n1'], interface['n2']# 计算不同偏振的反射率R_TE = []R_TM = []T_TE = []T_TM = []critical_angle = Nonefor theta_i in theta_i_rad:# 检查全反射if n1 > n2 and theta_i > np.arcsin(n2/n1):R_TE.append(1.0)R_TM.append(1.0)T_TE.append(0.0)T_TM.append(0.0)if critical_angle is None:critical_angle = np.degrees(theta_i)else:r_te, t_te, theta_t_te = fresnel_coefficients(n1, n2, theta_i, 'TE')r_tm, t_tm, theta_t_tm = fresnel_coefficients(n1, n2, theta_i, 'TM')R_te, T_te = reflectance_transmittance(r_te, t_te, n1, n2, theta_i, theta_t_te, 'TE')R_tm, T_tm = reflectance_transmittance(r_tm, t_tm, n1, n2, theta_i, theta_t_tm, 'TM')R_TE.append(R_te)R_TM.append(R_tm)T_TE.append(T_te)T_TM.append(T_tm)row, col = i // 2, i % 2# 绘制反射率axes[row, col].plot(theta_i_deg, R_TE, 'b-', linewidth=2, label='R_TE (s偏振)')axes[row, col].plot(theta_i_deg, R_TM, 'r-', linewidth=2, label='R_TM (p偏振)')axes[row, col].plot(theta_i_deg, T_TE, 'b--', linewidth=2, label='T_TE', alpha=0.7)axes[row, col].plot(theta_i_deg, T_TM, 'r--', linewidth=2, label='T_TM', alpha=0.7)# 标记布鲁斯特角 (p偏振反射率为0)if n1 < n2:  # 从光疏到光密brewster_angle = np.degrees(np.arctan(n2/n1))axes[row, col].axvline(x=brewster_angle, color='red', linestyle=':', alpha=0.7, label=f'布鲁斯特角 {brewster_angle:.1f}°')# 标记临界角if critical_angle is not None:axes[row, col].axvline(x=critical_angle, color='green', linestyle=':', alpha=0.7, label=f'临界角 {critical_angle:.1f}°')axes[row, col].set_xlabel('入射角 (度)')axes[row, col].set_ylabel('反射率/透射率')axes[row, col].set_title(f'{interface["name"]} (n1={n1}, n2={n2})')axes[row, col].legend()axes[row, col].grid(True, alpha=0.3)axes[row, col].set_ylim(0, 1.1)plt.tight_layout()plt.show()# 布儒斯特角详细分析print("布儒斯特角分析:")n2_values = np.linspace(1.1, 3.0, 50)brewster_angles = np.degrees(np.arctan(n2_values))  # n1=1.0plt.figure(figsize=(10, 6))plt.plot(n2_values, brewster_angles, 'b-', linewidth=2)plt.xlabel('折射率 n₂')plt.ylabel('布儒斯特角 (度)')plt.title('布儒斯特角随折射率变化 (n₁=1.0)')plt.grid(True, alpha=0.3)# 标记常见材料common_materials = {'水 (1.33)': 1.33,'玻璃 (1.5)': 1.5,'钻石 (2.4)': 2.4}for name, n in common_materials.items():angle = np.degrees(np.arctan(n))plt.plot(n, angle, 'ro', markersize=8)plt.text(n, angle + 2, f'{name}\n{angle:.1f}°', ha='center', fontsize=10)plt.show()return interfacesdef total_internal_reflection():"""全反射现象"""# 从光密到光疏介质n1, n2 = 1.5, 1.0  # 玻璃到空气critical_angle = np.degrees(np.arcsin(n2/n1))print(f"临界角: {critical_angle:.2f}°")# 入射角范围theta_i_deg = np.linspace(0, 90, 100)theta_i_rad = np.radians(theta_i_deg)# 计算反射系数（复数，用于全反射情况）def complex_fresnel_TE(n1, n2, theta_i):"""全反射情况下的复数菲涅耳系数 (TE)"""sin_theta_t = n1 * np.sin(theta_i) / n2if sin_theta_t <= 1:# 正常折射theta_t = np.arcsin(sin_theta_t)r = (n1 * np.cos(theta_i) - n2 * np.cos(theta_t)) / (n1 * np.cos(theta_i) + n2 * np.cos(theta_t))return r, 0else:# 全反射cos_theta_t = 1j * np.sqrt(sin_theta_t**2 - 1)  # 虚数r = (n1 * np.cos(theta_i) - n2 * cos_theta_t) / (n1 * np.cos(theta_i) + n2 * cos_theta_t)phase_shift = np.angle(r)return np.abs(r), phase_shift# 计算反射系数和相位移动R_TE = []phase_TE = []for theta_i in theta_i_rad:r_mag, phase = complex_fresnel_TE(n1, n2, theta_i)R_TE.append(r_mag**2)phase_TE.append(phase)# 绘制结果fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# 反射率ax1.plot(theta_i_deg, R_TE, 'b-', linewidth=2)ax1.axvline(x=critical_angle, color='red', linestyle='--', label=f'临界角 {critical_angle:.1f}°')ax1.set_xlabel('入射角 (度)')ax1.set_ylabel('反射率 R')ax1.set_title('全反射现象 - 反射率')ax1.legend()ax1.grid(True, alpha=0.3)# 相位移动ax2.plot(theta_i_deg, np.degrees(phase_TE), 'r-', linewidth=2)ax2.axvline(x=critical_angle, color='red', linestyle='--', label=f'临界角 {critical_angle:.1f}°')ax2.set_xlabel('入射角 (度)')ax2.set_ylabel('相位移动 (度)')ax2.set_title('全反射现象 - 相位移动')ax2.legend()ax2.grid(True, alpha=0.3)plt.tight_layout()plt.show()# 倏逝波分析print("\n倏逝波分析:")z = np.linspace(0, 1, 200)  # 进入第二介质的深度theta_i_example = np.radians(60)  # 大于临界角的入射角# 衰减常数k0 = 2 * np.pi / (500e-9)  # 假设波长500nmkappa = k0 * n1 * np.sqrt(np.sin(theta_i_example)**2 - (n2/n1)**2)# 倏逝场evanescent_field = np.exp(-kappa * z)plt.figure(figsize=(10, 6))plt.plot(z*1e9, evanescent_field, 'b-', linewidth=2)plt.axhline(y=1/np.e, color='red', linestyle='--', label=f'1/e 深度: {1e9/kappa:.1f} nm')plt.xlabel('深度 z (nm)')plt.ylabel('倏逝场强度')plt.title('倏逝波衰减 (θ_i = 60°)')plt.legend()plt.grid(True, alpha=0.3)plt.yscale('log')plt.show()return critical_angle# 运行反射折射分析
interfaces = reflection_refraction()
critical_angle = total_internal_reflection()

2.4.2 运行结果

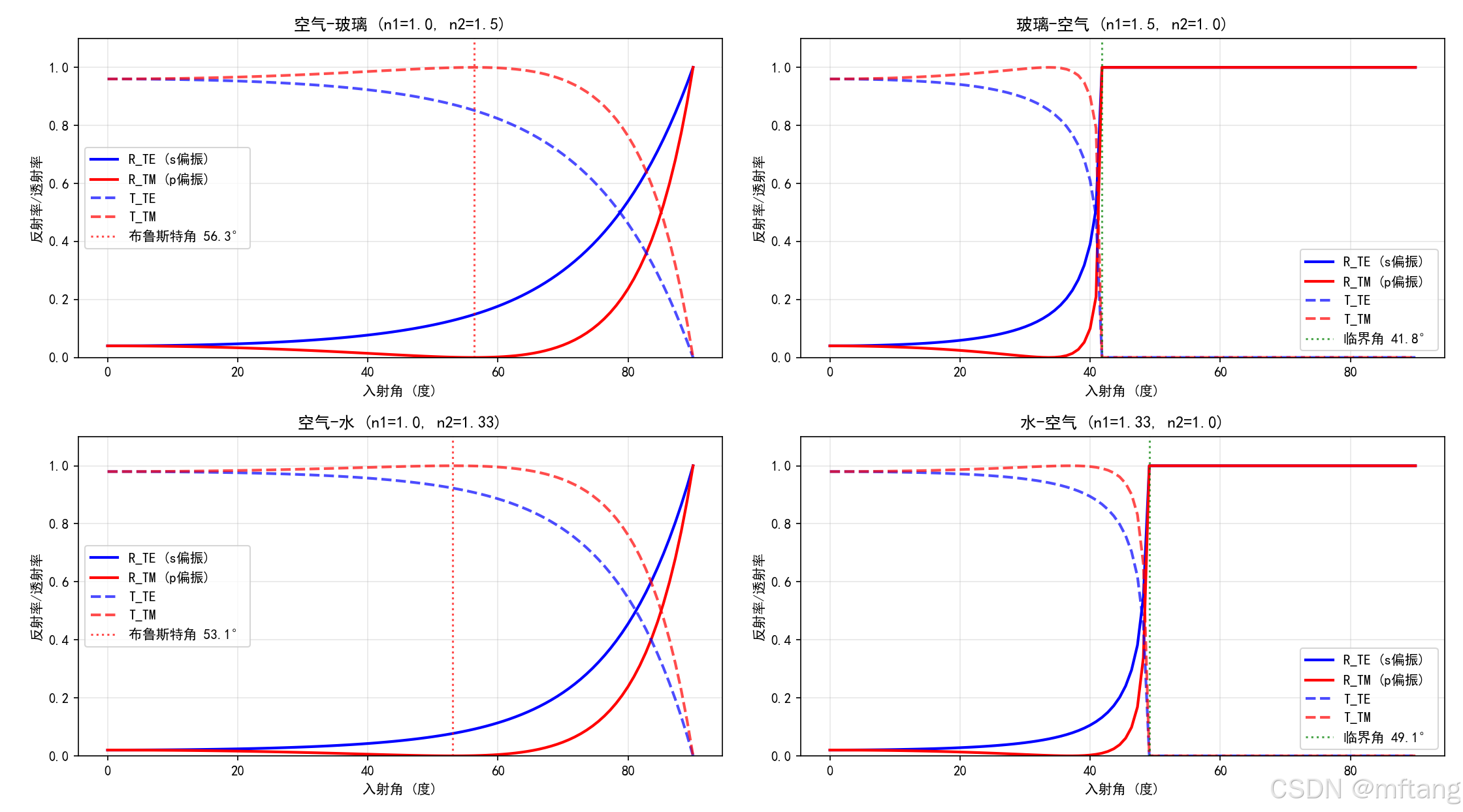
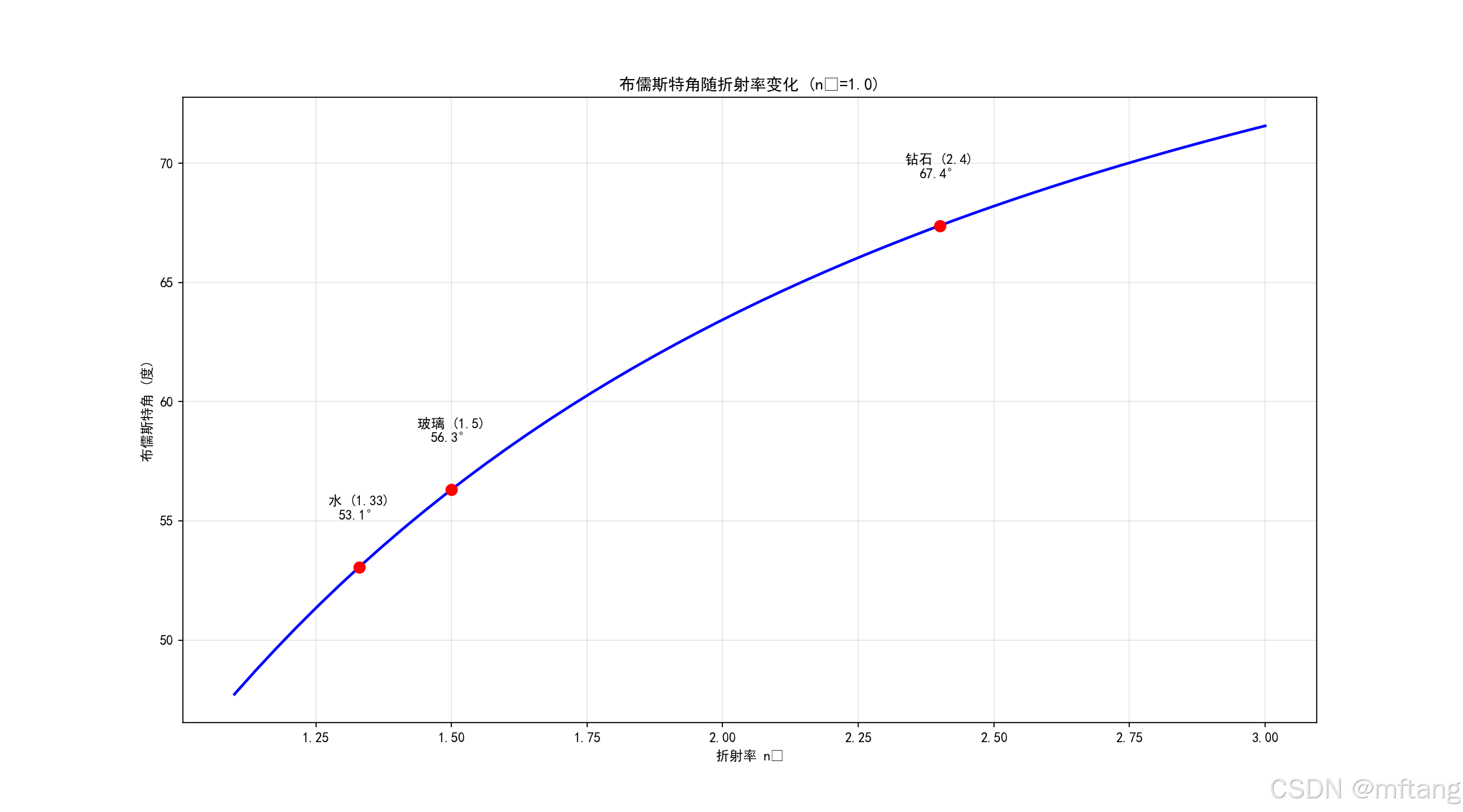
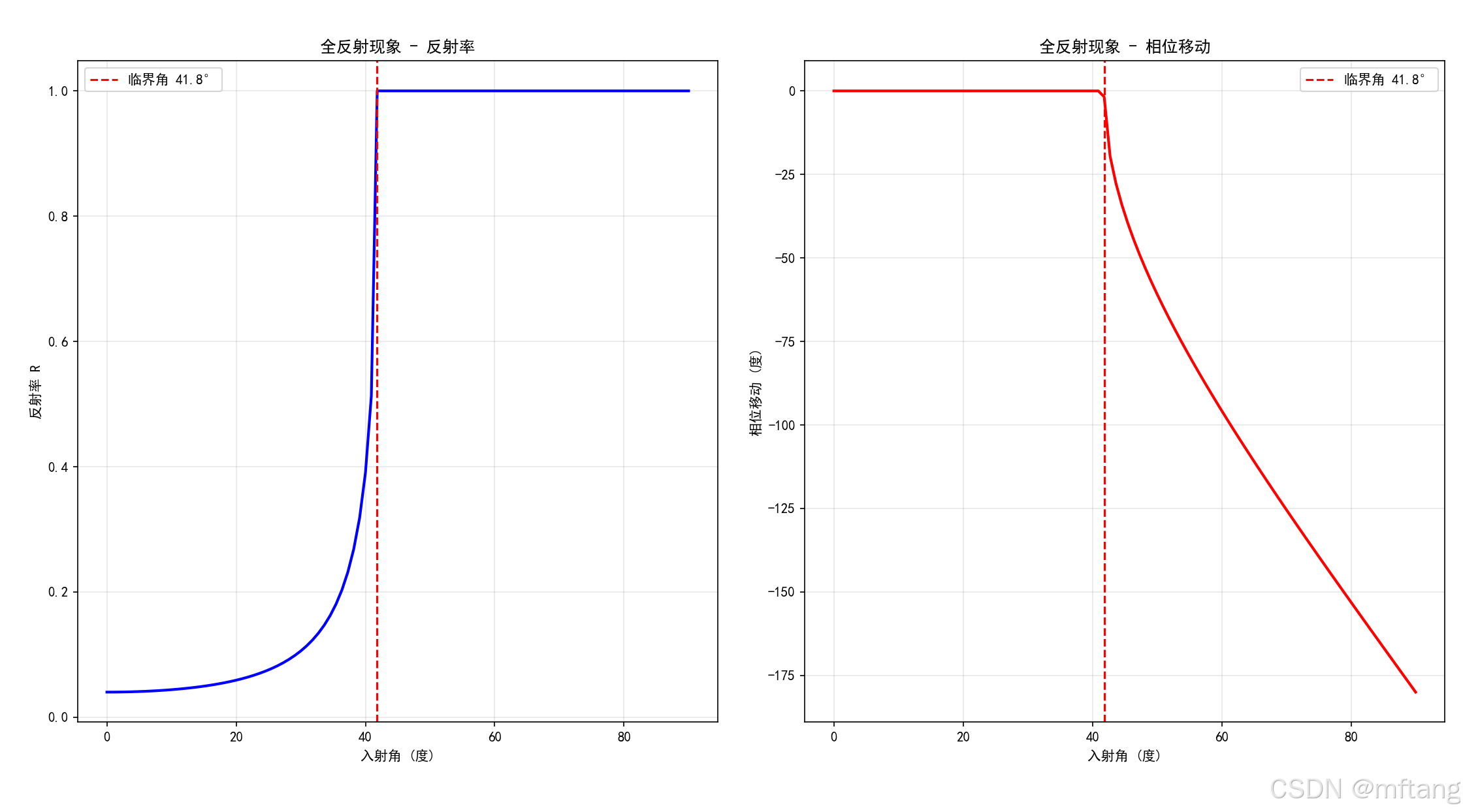
2.5 波导和谐振腔

波导：约束电磁波传播的结构

截止频率：低于此频率不能传播

模式：不同的场分布形式

2.5.1 代码实现

def waveguide_modes():"""波导模式分析"""def rectangular_waveguide_modes(a, b, f, m, n, epsilon_r=1.0, mu_r=1.0):"""矩形波导模式分析a, b: 波导尺寸 (m)f: 频率 (Hz)m, n: 模式指数"""c = constants.c / np.sqrt(epsilon_r * mu_r)k = 2 * np.pi * f / c# 截止波数kc = np.sqrt((m * np.pi / a)**2 + (n * np.pi / b)**2)# 截止频率fc = c * kc / (2 * np.pi)# 传播常数if f > fc:beta = np.sqrt(k**2 - kc**2)  # 传播模式gamma = 1j * beta  # 传播常数else:beta = 0gamma = np.sqrt(kc**2 - k**2)  # 衰减模式# 波导波长lambda_g = 2 * np.pi / beta if beta > 0 else float('inf')# 相速度vp = c / np.sqrt(1 - (fc/f)**2) if f > fc else float('inf')# 群速度vg = c * np.sqrt(1 - (fc/f)**2) if f > fc else 0return {'cutoff_frequency': fc,'propagation_constant': beta,'guide_wavelength': lambda_g,'phase_velocity': vp,'group_velocity': vg}# 标准矩形波导 (WR-90)a = 22.86e-3  # 宽边尺寸b = 10.16e-3  # 窄边尺寸print(f"矩形波导 WR-90:")print(f"尺寸: {a*1000:.2f} × {b*1000:.2f} mm")# 不同模式的截止频率modes = [(1,0), (2,0), (0,1), (1,1), (2,1), (3,0)]print("\n模式截止频率:")for m, n in modes:if m == 0 and n == 0:continue  # TEM模在波导中不存在mode_info = rectangular_waveguide_modes(a, b, 10e9, m, n)print(f"TE{m}{n}模: fc = {mode_info['cutoff_frequency']/1e9:.2f} GHz")# 色散关系frequencies = np.linspace(1e9, 20e9, 200)plt.figure(figsize=(12, 8))for m, n in [(1,0), (2,0), (0,1)]:vp_list = []vg_list = []lambda_g_list = []for f in frequencies:mode_info = rectangular_waveguide_modes(a, b, f, m, n)vp_list.append(mode_info['phase_velocity'])vg_list.append(mode_info['group_velocity'])lambda_g_list.append(mode_info['guide_wavelength'])# 标记截止频率fc = rectangular_waveguide_modes(a, b, 10e9, m, n)['cutoff_frequency']plt.subplot(2, 2, 1)plt.plot(frequencies/1e9, np.array(vp_list)/1e6, linewidth=2, label=f'TE{m}{n}')plt.axvline(x=fc/1e9, linestyle='--', alpha=0.5)plt.subplot(2, 2, 2)plt.plot(frequencies/1e9, np.array(vg_list)/1e6, linewidth=2, label=f'TE{m}{n}')plt.axvline(x=fc/1e9, linestyle='--', alpha=0.5)plt.subplot(2, 2, 3)plt.plot(frequencies/1e9, np.array(lambda_g_list)*100, linewidth=2, label=f'TE{m}{n}')plt.axvline(x=fc/1e9, linestyle='--', alpha=0.5)plt.subplot(2, 2, 1)plt.xlabel('频率 (GHz)')plt.ylabel('相速度 (×10⁶ m/s)')plt.title('波导相速度')plt.legend()plt.grid(True, alpha=0.3)plt.subplot(2, 2, 2)plt.xlabel('频率 (GHz)')plt.ylabel('群速度 (×10⁶ m/s)')plt.title('波导群速度')plt.legend()plt.grid(True, alpha=0.3)plt.subplot(2, 2, 3)plt.xlabel('频率 (GHz)')plt.ylabel('波导波长 (cm)')plt.title('波导波长')plt.legend()plt.grid(True, alpha=0.3)# 场分布可视化 (TE10模)x = np.linspace(0, a, 50)y = np.linspace(0, b, 50)X, Y = np.meshgrid(x, y)# TE10模的电场分布E_y = np.sin(np.pi * X / a)  # 只有y分量plt.subplot(2, 2, 4)plt.contourf(X*1000, Y*1000, E_y, levels=50, cmap='RdBu')plt.colorbar(label='电场 Ey')plt.xlabel('x (mm)')plt.ylabel('y (mm)')plt.title('TE10模电场分布')plt.gca().set_aspect('equal')plt.tight_layout()plt.show()return a, b, modesdef resonant_cavity():"""谐振腔分析"""def rectangular_cavity_resonance(a, b, d, m, n, p, epsilon_r=1.0, mu_r=1.0):"""矩形谐振腔谐振频率a, b, d: 腔体尺寸m, n, p: 模式指数"""c = constants.c / np.sqrt(epsilon_r * mu_r)# 谐振频率f_resonant = (c / 2) * np.sqrt((m/a)**2 + (n/b)**2 + (p/d)**2)return f_resonant# 标准谐振腔尺寸a, b, d = 10e-2, 5e-2, 8e-2  # 10cm × 5cm × 8cmprint(f"矩形谐振腔:")print(f"尺寸: {a*100:.1f} × {b*100:.1f} × {d*100:.1f} cm")# 主要模式的谐振频率cavity_modes = [(1,0,1), (0,1,1), (1,1,1), (2,0,1), (1,0,2)]print("\n谐振频率:")for m, n, p in cavity_modes:f_res = rectangular_cavity_resonance(a, b, d, m, n, p)print(f"TE{m}{n}{p}模: f = {f_res/1e9:.2f} GHz")# 品质因数计算 (简化)def cavity_Q(f_res, conductivity=5.8e7, mu_r=1.0):"""谐振腔品质因数估算"""# 对于铜壁skin_depth = 1 / np.sqrt(np.pi * f_res * constants.mu_0 * conductivity)# 体积与表面积比 (简化计算)V = a * b * dS = 2*(a*b + a*d + b*d)# 品质因数 Q ≈ (体积/表面积) / skin_depthQ = V / (S * skin_depth)return Q# 品质因数分析conductivities = [5.8e7, 1e7, 1e6, 1e5]  # 不同材料的电导率materials = ['铜', '黄铜', '不锈钢', '铝']f_res_example = rectangular_cavity_resonance(a, b, d, 1, 0, 1)print(f"\nTE101模品质因数:")for cond, material in zip(conductivities, materials):Q = cavity_Q(f_res_example, conductivity=cond)print(f"{material}: Q = {Q:.0f}")# 谐振曲线frequencies = np.linspace(0.8*f_res_example, 1.2*f_res_example, 500)plt.figure(figsize=(10, 6))for cond, material in zip(conductivities, materials):Q = cavity_Q(f_res_example, conductivity=cond)# 谐振曲线 (洛伦兹型)response = 1 / np.sqrt(1 + Q**2 * ((frequencies/f_res_example) - (f_res_example/frequencies))**2)plt.plot(frequencies/1e9, response, linewidth=2, label=f'{material} (Q={Q:.0f})')plt.axvline(x=f_res_example/1e9, color='k', linestyle='--', alpha=0.5, label='谐振频率')plt.xlabel('频率 (GHz)')plt.ylabel('响应')plt.title('谐振腔频率响应')plt.legend()plt.grid(True, alpha=0.3)plt.show()return a, b, d, cavity_modes# 运行波导和谐振腔分析
waveguide_a, waveguide_b, waveguide_modes = waveguide_modes()
cavity_a, cavity_b, cavity_d, cavity_modes = resonant_cavity()

2.5.2 运行结果

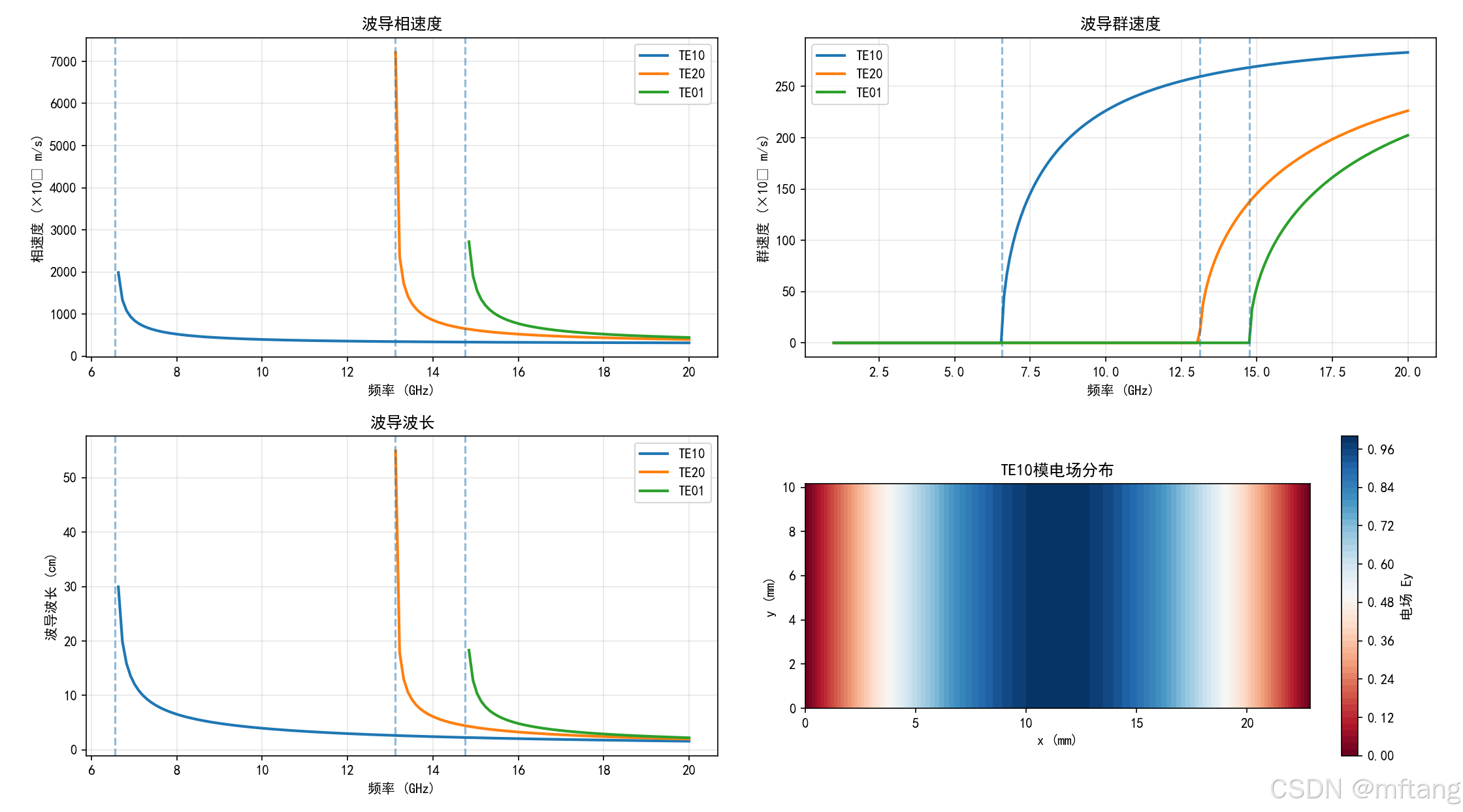
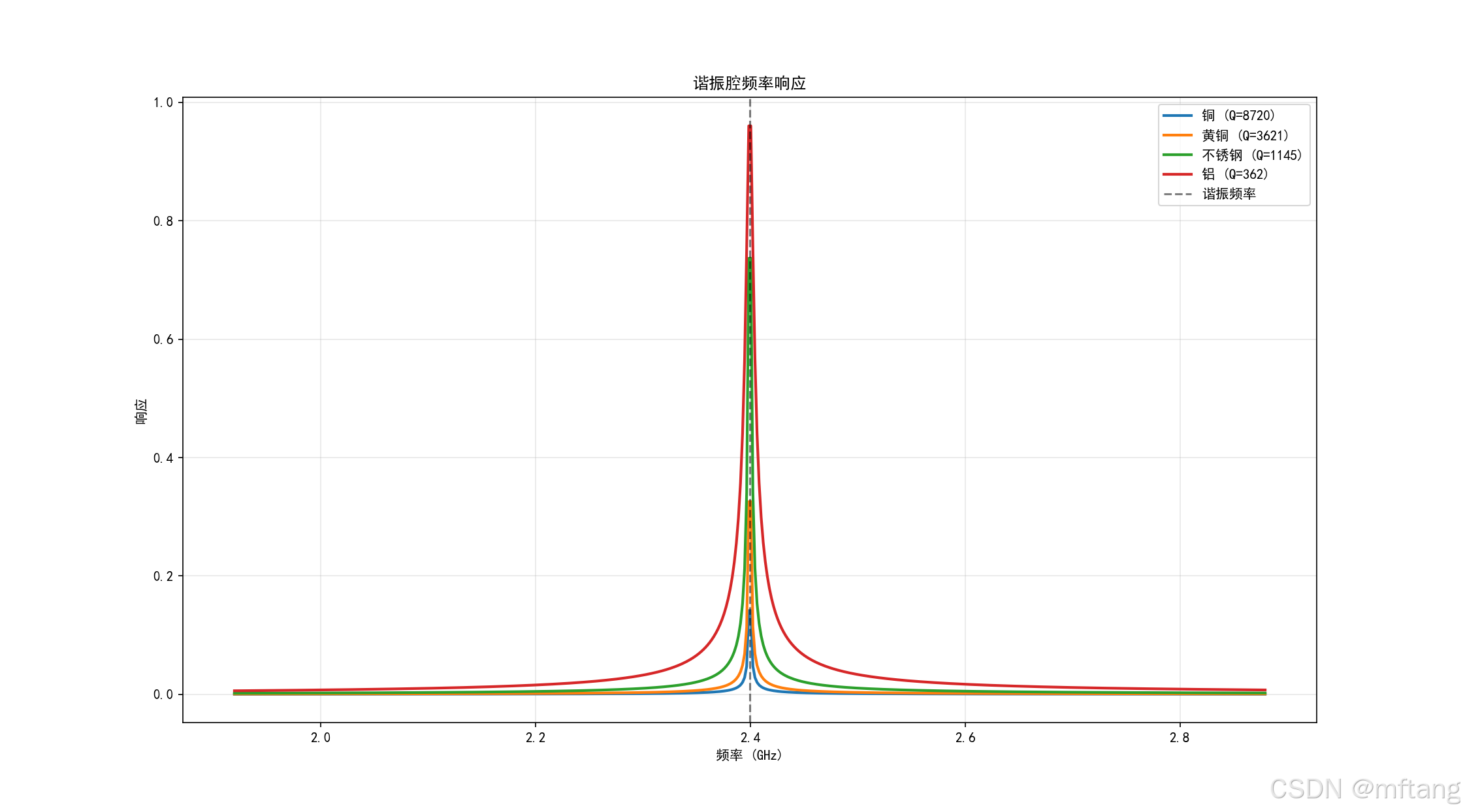
输出log：

矩形波导 WR-90:
尺寸: 22.86 × 10.16 mm模式截止频率:
TE10模: fc = 6.56 GHz
TE20模: fc = 13.11 GHz
TE01模: fc = 14.75 GHz
TE11模: fc = 16.15 GHz
TE21模: fc = 19.74 GHz
TE30模: fc = 19.67 GHz矩形谐振腔:
尺寸: 10.0 × 5.0 × 8.0 cm谐振频率:
TE101模: f = 2.40 GHz
TE011模: f = 3.54 GHz
TE111模: f = 3.84 GHz
TE201模: f = 3.54 GHz
TE102模: f = 4.04 GHzTE101模品质因数:
铜: Q = 8720
黄铜: Q = 3621
不锈钢: Q = 1145
铝: Q = 362

2.6 天线辐射

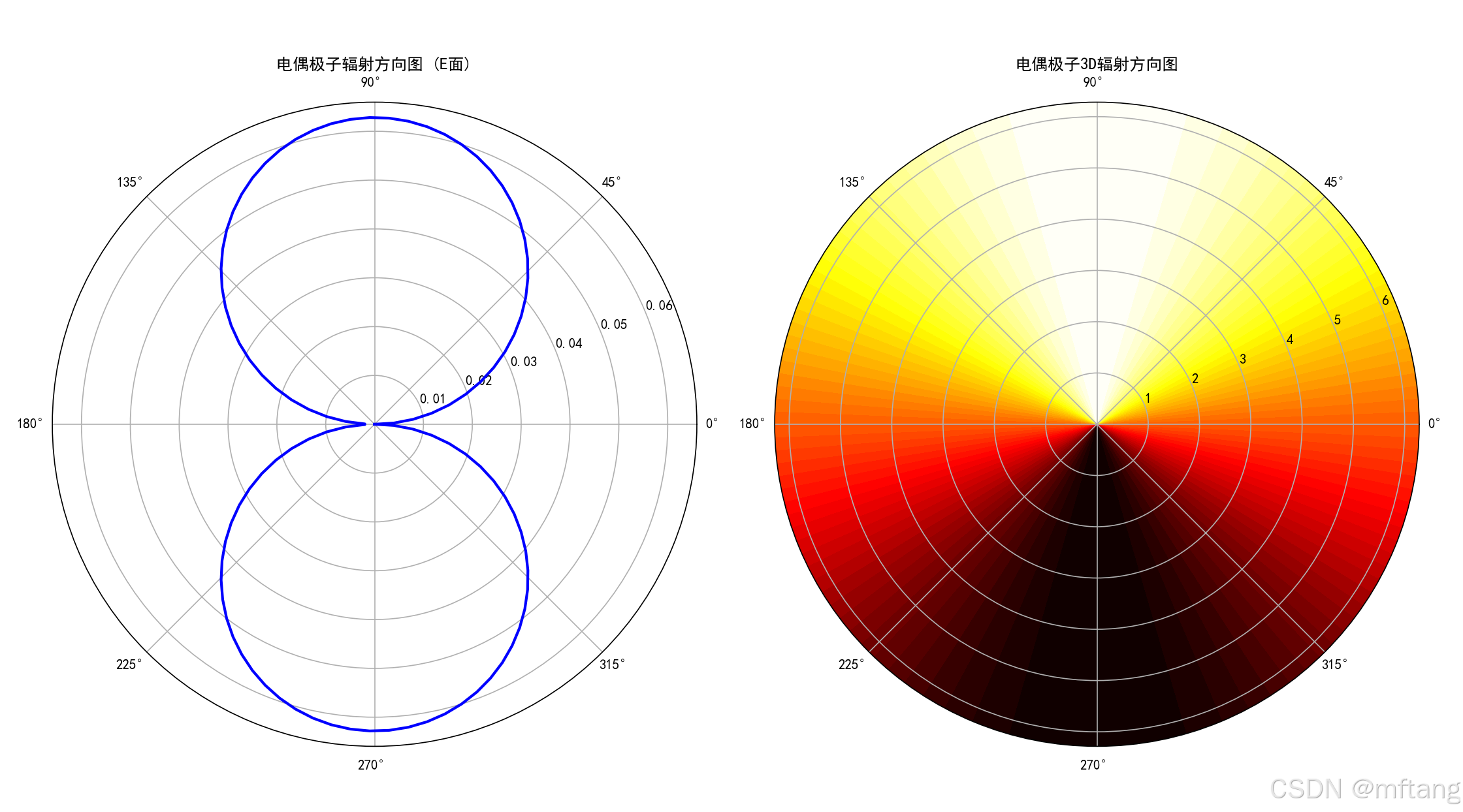
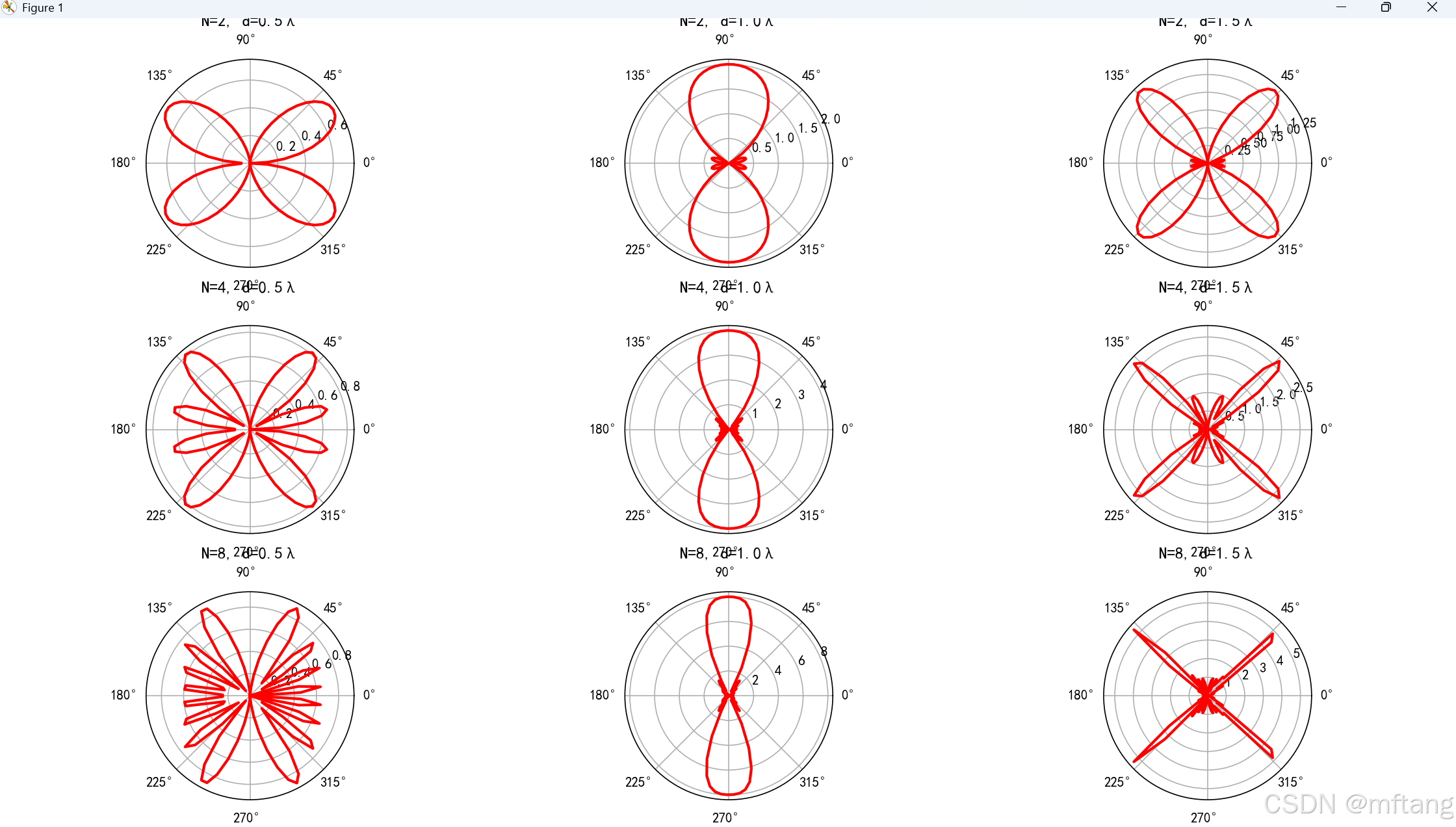
辐射方向图描述空间能量分布

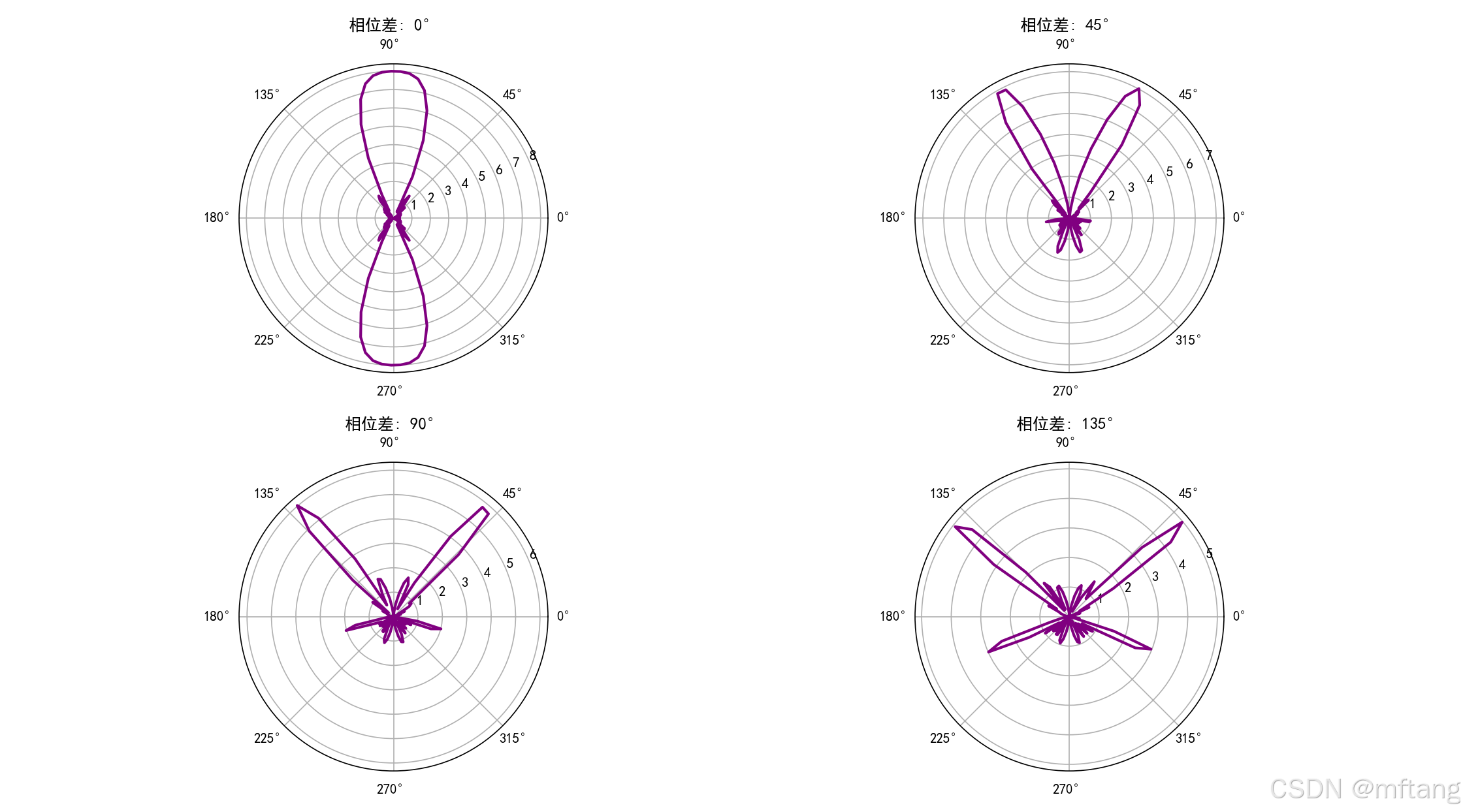
天线阵列实现波束形成和扫描

方向性衡量能量集中程度

2.6.1 代码实现

def antenna_radiation():"""天线辐射分析"""def dipole_radiation_pattern(I, l, f, r, theta):"""电偶极子辐射场I: 电流 (A)l: 偶极子长度 (m)f: 频率 (Hz)r: 距离 (m)theta: 角度 (弧度)"""c = constants.ck = 2 * np.pi * f / ceta = np.sqrt(constants.mu_0 / constants.epsilon_0)  # 自由空间阻抗# 远场近似E_theta = (1j * eta * k * I * l / (4 * np.pi * r)) * np.sin(theta) * np.exp(-1j * k * r)H_phi = E_theta / etareturn np.abs(E_theta), np.abs(H_phi)def antenna_array_factor(N, d, theta, phi, f, phase_diff=0):"""天线阵列因子N: 天线数量d: 天线间距theta, phi: 观察方向phase_diff: 相邻天线相位差"""c = constants.ck = 2 * np.pi * f / cpsi = k * d * np.sin(theta) * np.cos(phi) + phase_diffif N == 1:return 1else:if np.abs(psi) < 1e-10:return Nelse:return np.abs(np.sin(N * psi / 2) / np.sin(psi / 2))# 单偶极子辐射方向图I = 1.0  # 电流l = 0.1  # 偶极子长度f = 100e6  # 频率r = 100  # 观察距离theta = np.linspace(0, 2*np.pi, 100)E_pattern = []for th in theta:E, H = dipole_radiation_pattern(I, l, f, r, th)E_pattern.append(E)# 极坐标图fig, axes = plt.subplots(1, 2, figsize=(12, 5), subplot_kw={'projection': 'polar'})# 电场方向图axes[0].plot(theta, E_pattern, 'b-', linewidth=2)axes[0].set_title('电偶极子辐射方向图 (E面)')axes[0].grid(True)# 3D方向图theta_3d = np.linspace(0, 2*np.pi, 50)phi_3d = np.linspace(0, 2*np.pi, 50)Theta, Phi = np.meshgrid(theta_3d, phi_3d)# 偶极子在z方向，辐射方向图与phi无关R = np.sin(Theta)axes[1].contourf(Theta, Phi, R, levels=50, cmap='hot')axes[1].set_title('电偶极子3D辐射方向图')plt.tight_layout()plt.show()# 天线阵列分析print("天线阵列分析:")N_values = [2, 4, 8]  # 天线数量d_values = [0.5, 1.0, 1.5]  # 间距 (以波长为单位)wavelength = constants.c / ffig, axes = plt.subplots(3, 3, figsize=(15, 12), subplot_kw={'projection': 'polar'})for i, N in enumerate(N_values):for j, d_ratio in enumerate(d_values):d = d_ratio * wavelengtharray_pattern = []for th in theta:af = antenna_array_factor(N, d, th, 0, f)# 假设单元方向图为偶极子element_pattern = np.sin(th) if th <= np.pi else np.sin(2*np.pi - th)total_pattern = af * element_patternarray_pattern.append(total_pattern)axes[i, j].plot(theta, array_pattern, 'r-', linewidth=2)axes[i, j].set_title(f'N={N}, d={d_ratio}λ')axes[i, j].grid(True)plt.tight_layout()plt.show()# 波束扫描print("\n相控阵波束扫描:")phase_shifts = [0, np.pi/4, np.pi/2, 3*np.pi/4]plt.figure(figsize=(12, 8))for i, phase_shift in enumerate(phase_shifts):array_pattern = []for th in theta:af = antenna_array_factor(8, wavelength, th, 0, f, phase_shift)element_pattern = np.sin(th) if th <= np.pi else np.sin(2*np.pi - th)total_pattern = af * element_patternarray_pattern.append(total_pattern)plt.subplot(2, 2, i+1, projection='polar')plt.plot(theta, array_pattern, 'purple', linewidth=2)plt.title(f'相位差: {np.degrees(phase_shift):.0f}°')plt.grid(True)plt.tight_layout()plt.show()# 天线增益和方向性def antenna_directivity(radiation_pattern, theta):"""计算天线方向性"""# 总辐射功率total_power = np.trapz(radiation_pattern**2 * np.sin(theta), theta)# 最大辐射强度max_intensity = np.max(radiation_pattern**2)# 方向性 D = 4π * 最大辐射强度 / 总辐射功率directivity = 4 * np.pi * max_intensity / total_powerreturn directivitydirectivity = antenna_directivity(E_pattern, theta)print(f"电偶极子方向性: D = {directivity:.2f} ({10*np.log10(directivity):.1f} dBi)")# 不同天线的方向性比较antenna_types = {'各向同性': [1] * len(theta),'电偶极子': E_pattern,'半波偶极子': [np.abs(np.cos(np.pi/2 * np.cos(th)) / np.sin(th)) if th !=0 and th != np.pi else 1 for th in theta]}plt.figure(figsize=(10, 6))for name, pattern in antenna_types.items():directivity = antenna_directivity(pattern, theta)plt.plot(theta, pattern, linewidth=2, label=f'{name} (D={directivity:.2f})')plt.xlabel('角度 θ (弧度)')plt.ylabel('归一化辐射强度')plt.title('不同类型天线的辐射方向图')plt.legend()plt.grid(True, alpha=0.3)plt.show()return E_pattern, antenna_types# 运行天线辐射分析
dipole_pattern, antenna_types = antenna_radiation()