【大数据技术05】数据加工
参考资料:朝乐门。数据科学导论 [M]. 北京:人民邮电出版社,2020.
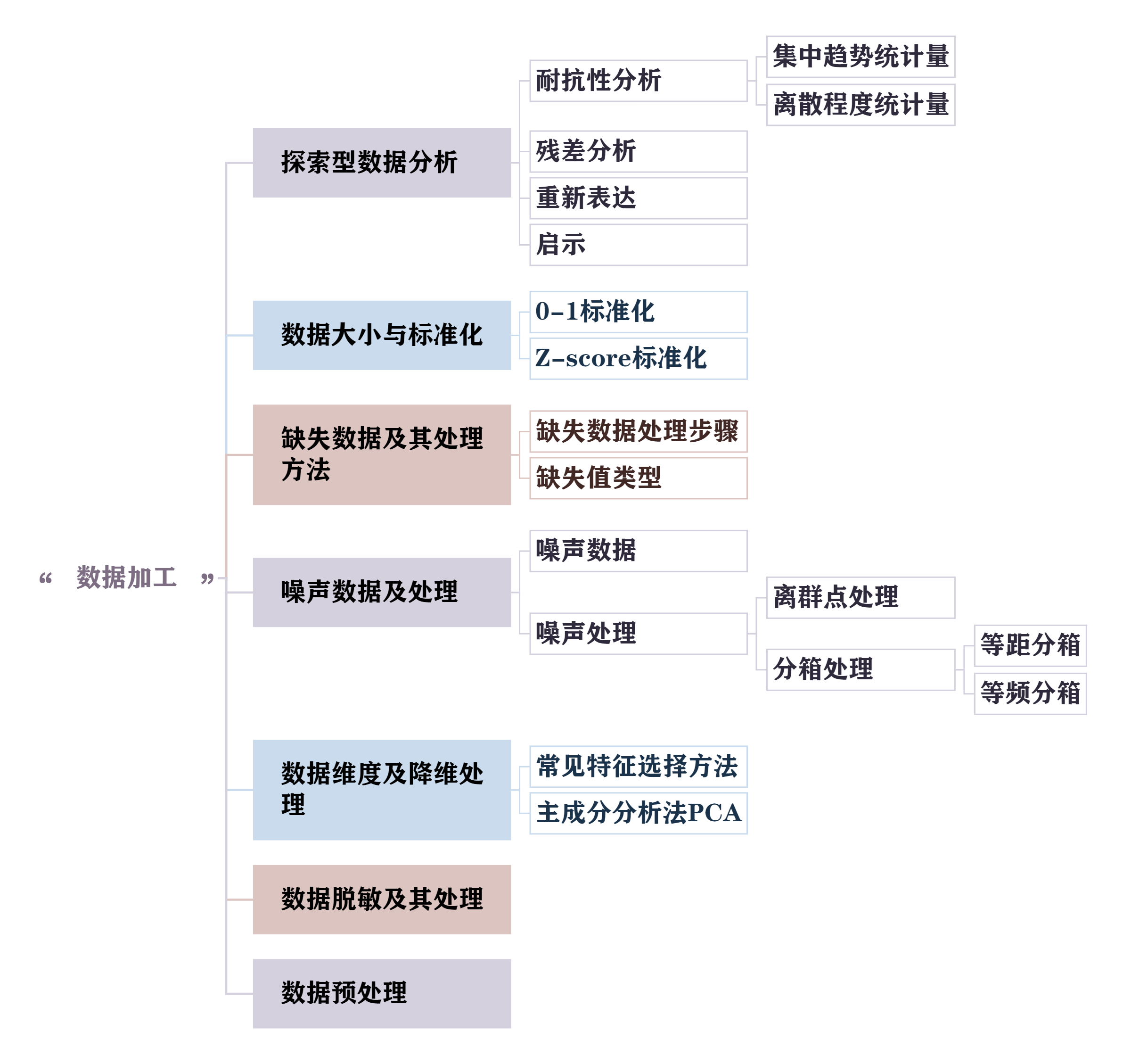
文章目录
- 五.数据加工
- 1. 探索型数据分析
- 1.1 耐抗性分析
- 1.2 残差分析
- 1.3 重新表达
- 4.启示
- 2.数据大小与标准化
- 2.1 0-1标准化
- 2.2 Z-score标准化
- 3.缺失数据及其处理方法
- 3.1 缺失数据处理步骤
- 3.2 缺失值类型
- 4.噪声数据及处理
- 4.1 噪声数据
- 4.2 离群点处理
- 4.3 分箱处理
- 5.数据维度及降维处理
- 5.1 常见的特征选择方法
- 5.2 特征创建方法PCA
- 主成分分析法PCA:“创造新特征”(特征提取)
- 6.数据脱敏及其处理
- 7.数据预处理方法
五.数据加工
1. 探索型数据分析
探索型数据分析主题
通常,探索型数据分析是数据加工的第一步
探索型数据分析(Exploratory Data Analysis,EDA)指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索,并通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。
“先验假定” 指在分析数据前,基于经验、直觉或理论预设的 “数据应该是什么样” 的判断
1.1 耐抗性分析
耐抗性是指对于数据的局部不良行为的非敏感性,他是探索性数据分析追求的主要目标
数据科学家重视耐抗性的主要原因在于“好”的数据也难免有差错甚至是重大差错。因此,进行数据分析时要有预防大错的破坏性影响的措施。
Eg.
中位数平滑是一种耐抗技术,而中位数是高耐抗性统计量
“耐抗性”(Resistance)是探索型数据分析(EDA)里很核心的一个概念,简单说就是数据分析方法或统计量 “抗干扰” 的能力—— 面对数据里的局部错误、极端值(比如录入错的异常数据、个别离谱的观测值),它不会轻易被带偏,还能保持对数据真实规律的判断。
比如我们熟悉的 “中位数” 就是典型的高耐抗性统计量:假设一组数据是 [2,3,4,5,6],中位数是 4;如果其中一个数据出错变成 [2,3,4,5,1000],中位数还是 4,完全没受极端值 1000 的影响。但如果用 “平均值”(低耐抗性),原本均值是 4,出错后均值直接变成 203,一下就被极端值带偏了。
探索型数据分析中常用的耐抗性分析统计量可以分为:集中趋势、离散程度、分布状态和频度等四类
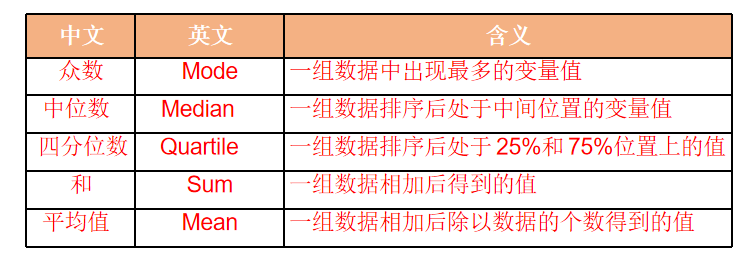
- 集中趋势统计量
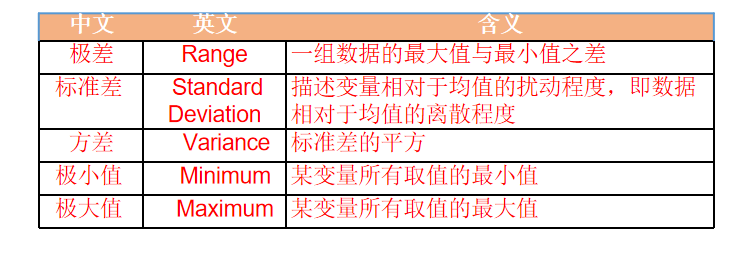
- 离散程度统计量
- 数据分布状态统计量
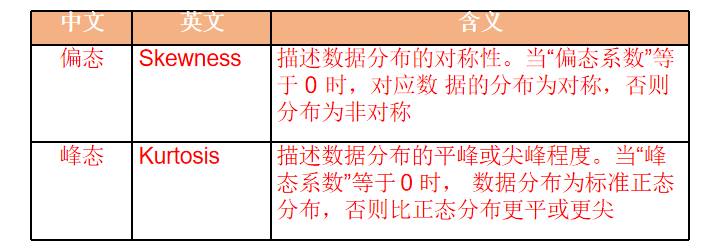
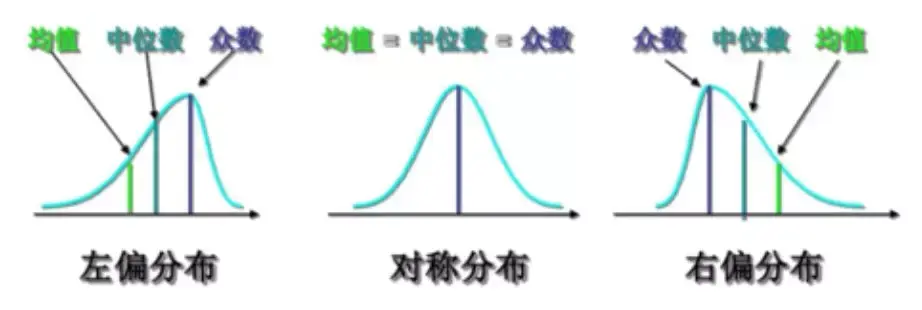
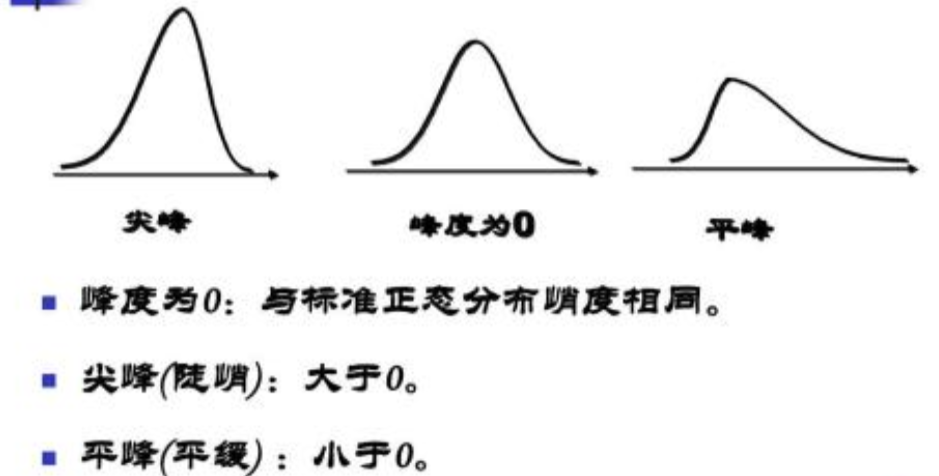
偏态分布有两种,左偏和右偏。长尾在哪边就是哪偏,下面第一张图的长尾在左边就是左偏,最后一张图的长尾在右边就是右偏。
1.2 残差分析
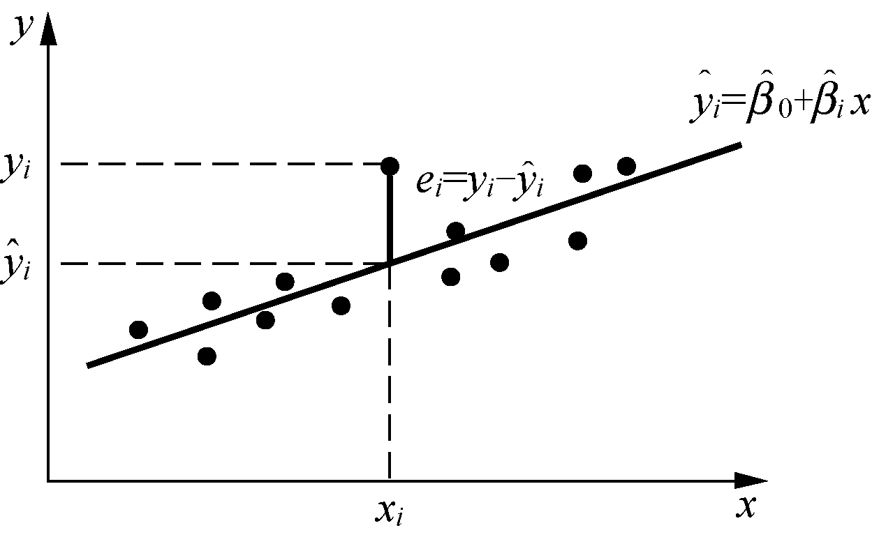
残差(Residuals):指数据减去一个总括统计量或者模型拟合值的才与部分
即:
残差=实际值−拟合值残差 = 实际值 - 拟合值 残差=实际值−拟合值
如果我们对数据集 Y 进行分析后得到拟合函数 yˆ = a + bx ,则在 xi 处对应两个值, 即实际值(yi)和拟合值( yˆi )。因此,xi 处的残差 ei = yi - yˆi ,如上图所示。
核心是通过对比 “数据实际值” 和 “模型拟合值” 的差异,帮我们判断模型是否贴合数据规律,或数据是否存在异常,
1.3 重新表达
重新表达(Re-Expression):是指找到合适的尺度或数据表达方式进行一定的转换,使得数据有利于简化分析
探索型数据分析强调,应尽早考虑数据的原始尺度是否合适的问题。如果尺度不合适,重新表达成另一个尺度可能更有助于促进对称性、变异恒定性、关系直线性或效应的可加性等。
重新表达也称变换(Transformation),一批数据 x1, x2, …, xn 的变换是一个函数 T,它把每个 xi 用新值 T(xi)来代替,使变换后的数据值是 T(x1), T(x2), …, T(xn )
原始数据有时会有 “不好用” 的问题,比如:
数据分布太偏(比如收入数据,大部分人低、少数人极高,直接分析难抓规律);
变量间关系不是直线(比如销量和广告投入是 “先快后慢” 的非线性关系,不好用线性模型分析);
数据波动差异大(比如小数值波动小、大数值波动大,影响计算稳定性)。
这时候就需要 “重新表达”,把数据调整成更适合分析的样子。
重新表达的核心:“找个合适的转换方式”
本质是用一个函数(比如 T (x))把原始数据 x 换成新数据 T (x),常见的简单转换有:
- 取对数(比如对收入数据取 ln (x)):能让偏态分布变平缓,缩小极端值的影响;
- 开平方(比如对计数数据√x):适合数据波动随数值增大而变大的情况;
- 倒数(比如对速度数据 1/x):适合 “数值越大、关联越弱” 的非线性关系。
4.启示
启示是指通过探索性数据分析,发现新的规律、问题等,进而满足数据加工和数据分析的需要
在探索型数据分析(EDA)里,“启示” 是整个分析过程的 “核心产出”—— 简单说,就是通过作图、算特征量、残差分析等手段探索数据后,发现的新规律、隐藏问题或有价值的线索,这些发现会直接指导后续的数据分析或决策。
- 分析用户消费数据时,通过画时间序列图发现 “每周五晚消费额骤增”,这就是一个 “启示”—— 后续可以针对周五晚设计促销活动
2.数据大小与标准化
标准化处理是数据大小变换的最常用方法之一。
数据标准化处理(Data Normalization)的目的是将数据按比例缩放,使之落入一个小的特定区间内。
在某些比较和评价类的指标处理中经常需要去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
2.1 0-1标准化
0-1 标准化(0-1 Normalization)指对原始数据的线性变换,使结果落到[0, 1], 转换函数如下:
x∗=x−MinMax−Minx^* = \frac{x - \text{Min}}{\text{Max} - \text{Min}} x∗=Max−Minx−Min
其中,Max 和 Min 分别为样本数据的最大值和最小值;x 与 x*分别代表标准化处理前的值和标准化处理后的值。
Min-Max标准化比较简单,但也存在一些缺陷—当有新数据加入时,可能导致最大值和最小值变化,需要重新定义 Min 和 Max 的取值。
2.2 Z-score标准化
(Zero-Score Normalization)指使经过处理的数据符合标准正态分布,即均值为 0,标准差为1,其转化函数为:
z=x−mσz = \frac{x - m}{\sigma} z=σx−m
其中 m为平均数,σ 为标准差,x 与 z 分别代表标准化处理前的值和标准化处理后 的值。
Min-Max 标准化/0-1标准化
- 核心特点:将数据线性映射到 [0, 1] 区间,保留数据的原始分布形状,仅压缩范围。
- 适用场景
- 需要 “绝对占比” 的场景:比如电商商品评分(0-5 分)标准化后直观体现 “相对高低”,或图像处理中像素值归一化(统一到 0-255 区间)。
- 算法对 “数据范围敏感” 的场景:如 K 近邻(KNN)、神经网络(需输入在 0-1 区间提升收敛性)、支持向量机(SVM,避免量纲差异主导距离计算)。
- 数据分布无明显极端值:若数据存在极大 / 极小异常值,Min-Max 会因 “极值主导区间” 导致大部分数据被压缩到很小范围(失去区分度)。
Z-score 标准化
- 核心特点:将数据转换为均值为 0、标准差为 1 的标准正态分布,突出数据的 “相对位置”(偏离均值的程度)。
- 适用场景
- 关注 “相对波动” 的场景:比如金融市场分析(某支股票收益率与市场平均收益率的偏离程度)、成绩排名(某学生分数与班级平均分的差距)。
- 数据存在极端值:通过 “除以标准差” 削弱极端值的影响(如用户消费数据中少数高消费用户不会主导分析)。
- 算法对 “分布形状” 敏感的场景:如主成分分析(PCA,需数据近似正态分布提升降维效果)、线性回归(消除量纲差异后系数更具解释性)。
总的来说:
- 若需要 **“0-1 区间的绝对占比”或算法对 “范围” 敏感 ** → 选 Min-Max 标准化;
- 若需要 **“相对波动的比较”或数据有极端值 ** → 选 Z-score 标准化。
Eg.
举个直观例子:比较学生 “身高” 和 “体重” 时,Z-score 能体现 “某学生身高比均值高 1 个标准差,体重比均值高 2 个标准差”,而 Min-Max 能体现 “该学生身高在班级排前 20%,体重排前 10%”—— 两者视角不同,按需选择即可。
3.缺失数据及其处理方法
3.1 缺失数据处理步骤
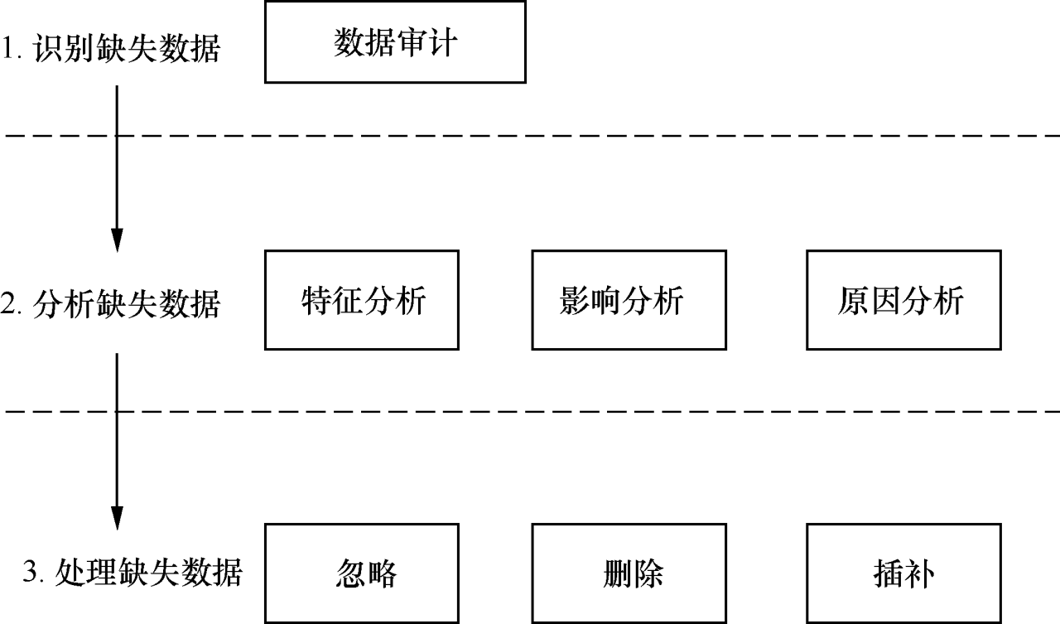
根据缺失数据对分析结果的影响及导致数据缺失的影响因素, 选择具体的缺失数据处理策略
- 识别缺失数据(数据审计)
通过 “数据审计” 环节,先定位数据中哪些位置存在缺失(比如某条记录的 “年龄” 字段为空、某用户的 “消费金额” 未记录等)。这是处理缺失数据的第一步,相当于 “先找到问题在哪里”。
- 分析缺失数据(特征、影响、原因分析)
特征分析:研究缺失数据的分布规律(比如是随机缺失,还是集中在某类人群 / 某类场景下);
影响分析:评估缺失数据对后续分析(如建模、统计)的干扰程度(比如少量缺失可能影响小,大量缺失可能导致结果失真);
原因分析:探究数据缺失的根源(是采集失误、用户未填写,还是业务逻辑导致的合理缺失等)。
这一步是 “搞清楚缺失数据的性质和影响”,为后续处理策略提供依据。
- 处理缺失数据(忽略、删除、插补)
根据前两步的分析,选择合适的处理方式:
忽略:若缺失数据对分析影响极小,可直接跳过;
删除:若缺失数据无规律且量少,可删除包含缺失值的记录或字段;
插补:若缺失数据有规律或影响大,通过技术手段 “填补” 缺失值(比如用均值、中位数填充,或通过算法预测填充)。
这一步是 “解决缺失问题”,让数据能满足后续分析的要求。
3.2 缺失值类型
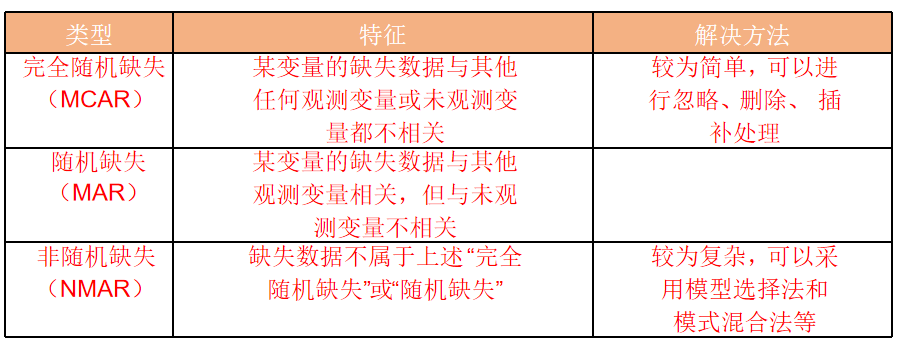
- MCAR:某变量的缺失数据和其他已观测、未观测的变量都没关系(纯随机缺失)。比如调查中 “年龄” 字段随机有几条没填,和其他问题的回答无关。
- MAR:变量的缺失数据和 “已观测的其他变量” 有关,但和 “未观测的变量” 无关。比如 “收入” 字段的缺失,和已观测的 “职业” 有关(比如自由职业者更可能不填收入),但和没观测的 “家庭背景” 无关。
- NMAR:缺失数据既不属于完全随机,也不属于随机缺失,是 “非随机” 的。比如 “心理健康评分” 的缺失,可能和 “评分本身较低(不想透露)” 有关,属于数据自身的隐藏规律导致的缺失。
4.噪声数据及处理
4.1 噪声数据
噪声:指的是测量变量中的随机错误或者误差
噪声数据分为三类:
- 错误数据
- 虚假数据
- 离群数据
4.2 离群点处理
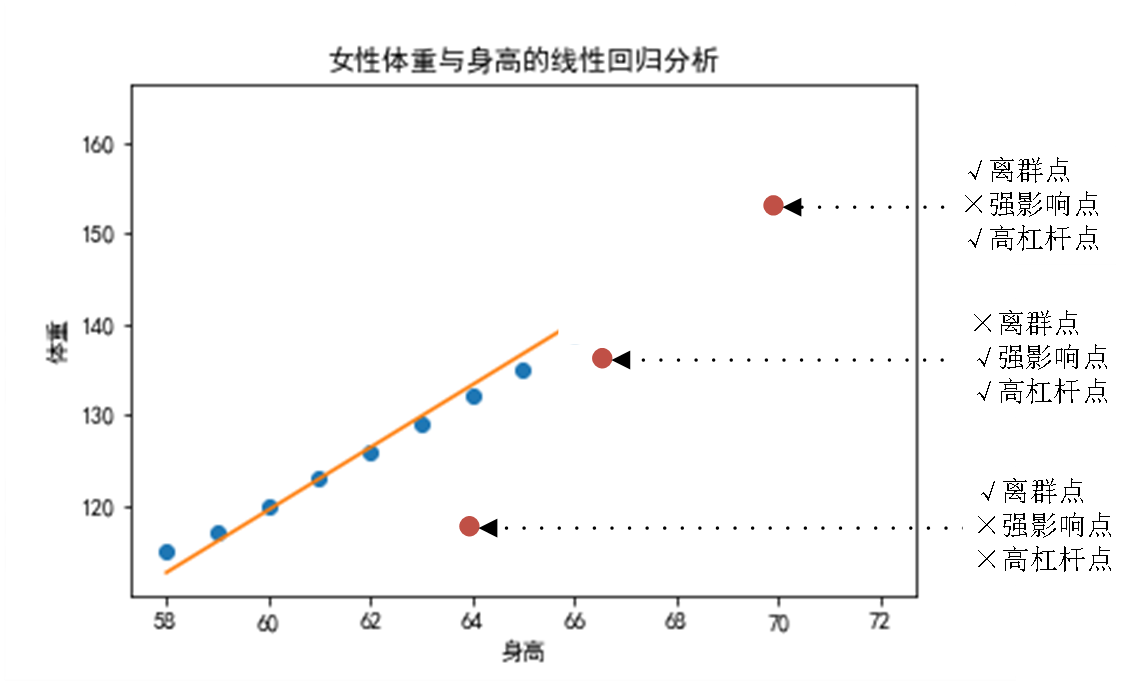
离群点(Outliers):是 数据集 中与其他数据偏离太大的点
离群点与高杠杆点(High Leverage)和强影响点(Influential Points)是3个既有联系又有区别。
高杠杆点(High Leverage Points):“自变量位置特殊,有‘撬动’模型的潜力”
离群点(Outliers):“自身数值异常,但不一定影响模型”
强影响点(Influential Points):“既特殊,又真的改变了模型”
常用的离群点的识别方法
-
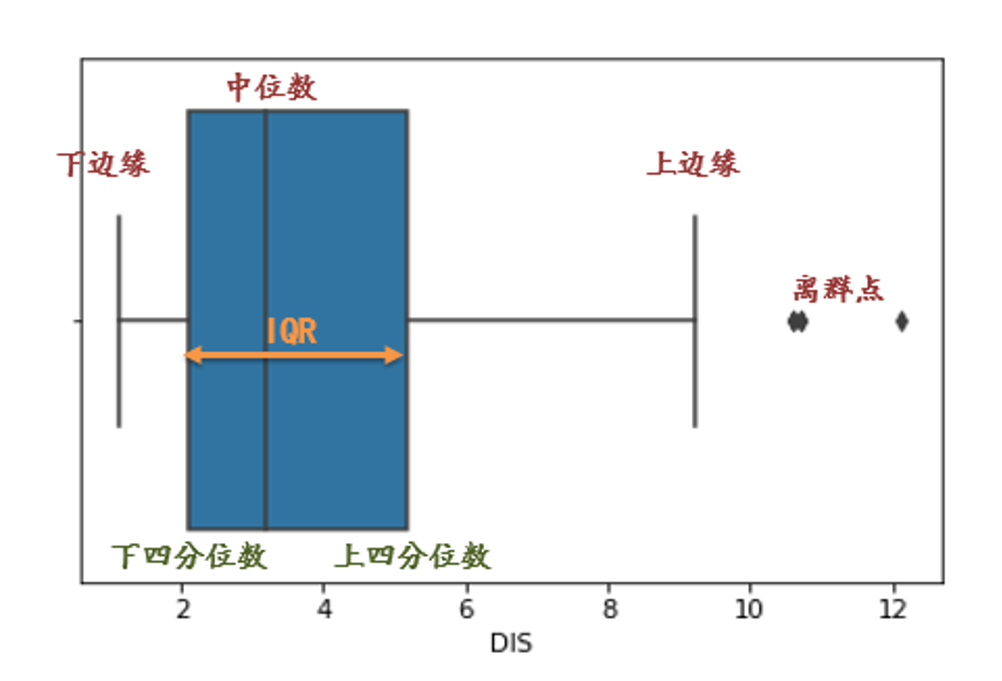
可视化方法:如上图所示的绘制散点图的方法;也可以采用箱线图方法,如下图
其中没有包含在箱线中的三个独立的点是离群点
-
四分位距法:
IQR:四分位距,代表了中间 50% 数据的范围,能反映数据的 “中间离散程度”
IQR=Q3−Q1\text{IQR} = Q_3 - Q_1 IQR=Q3−Q1
把数据从小到大排序后,分成 4 个相等的部分,产生 3 个分割点,这 3 个点就是四分位数:
下四分位数((Q_1)):数据的第 25% 分位数(25% 的数据小于它);
中位数((Q_2)):数据的第 50% 分位数(50% 的数据小于它);
上四分位数((Q_3)):数据的第 75% 分位数(75% 的数据小于它)
若一个数据点X属于:
X<(Q1−1.5×IQR)X< (Q_1 - 1.5 \times \text{IQR}) X<(Q1−1.5×IQR)
或:
X>(Q3+1.5×IQR)X> (Q_3 + 1.5 \times \text{IQR}) X>(Q3+1.5×IQR)
则X属于离群点
-
Z-score方法:通常将Z-score值在3倍以上的点视作离群点
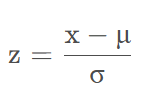
比如,若某数据的 Z-score 是 2,说明它比均值高 2 个标准差;若 Z-score 是 -1.5,说明它比均值低 1.5 个标准差。
-
聚类算法:如用DBSCAN、决策树、随机森林算法等发现离群点
4.3 分箱处理
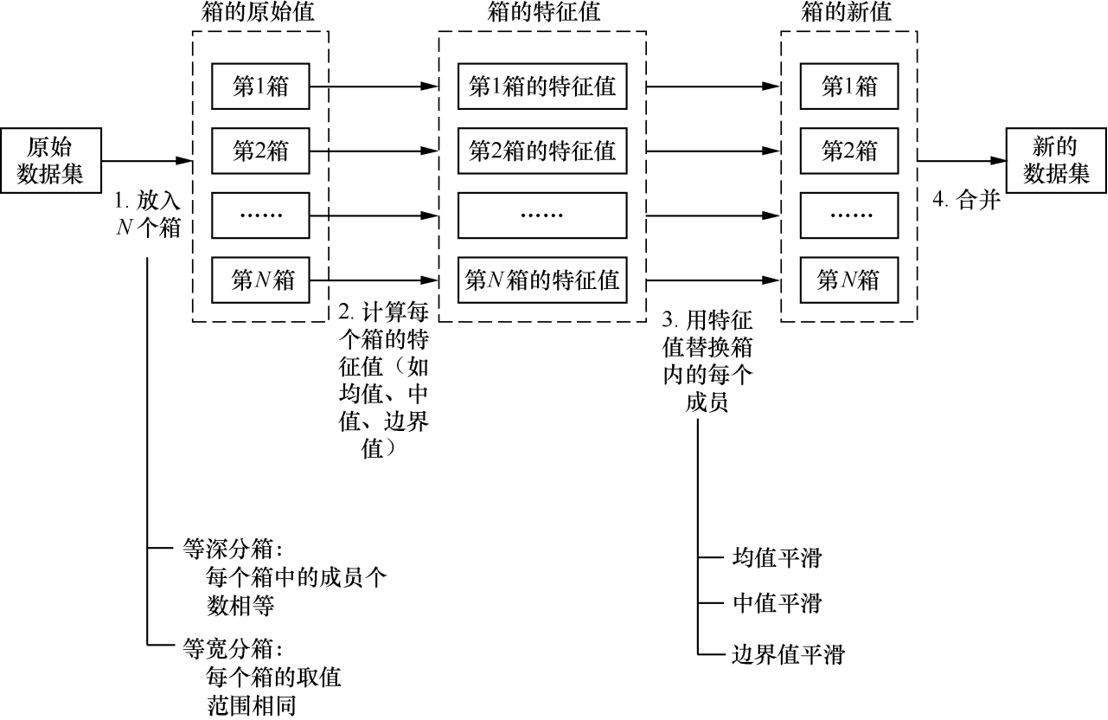
基本思路:分箱(Binning)处理的基本思路是将数据集放入若干个“箱子”之后,用每个箱子的均值(或边界值)替换该箱子内部的每个数据成员,进而达到噪声处理的目的
以数据集 Score={60, 65, 67, 72, 76, 77, 84, 87, 90}的噪声处理为例,其分箱处理过程如图所示
分箱处理(也叫离散化)是数据加工中的 “数据分组工具”,核心是把连续的数值型数据划分成若干个区间(“箱子”),让数据从 “连续” 变 “离散”,方便后续分析或建模
为什么要分箱?
连续数据有时会有 “太细、太散” 的问题,比如:
- 年龄数据(18、22、35…)直接分析难抓规律,但若分成 “青年(18-30)、中年(31-50)、老年(51+)” 就清晰多了;
- 某些算法(如决策树)对离散数据更友好,分箱后能提升模型效果;
- 可以削弱极端值的影响(比如把 “10000 元收入” 和 “9000 元收入” 都归到 “高收入” 箱)。
如何分箱?
- 等距分箱:把数据范围 “平均分” 成若干区间。比如把 0-100 的分数分成 “0-20、21-40、41-60、61-80、81-100”5 个箱,每个箱的区间长度相同。
- 等频分箱:让每个箱子里的数据数量差不多。比如把用户按消费金额分箱,确保每个箱里的用户数大致相等(适合数据分布不均的情况)。
(1)根据对原始数据集的分箱策略,分箱方法可以分为两种:
等深分箱(每个箱中的成员个数相等)
等宽分箱(每个箱的取值范围相同)。
(2)根据每个箱内成员数据的替换方法,分箱方法可以分为
-
均值平滑技术(用每个箱的均值代替箱内成员数据,如上例所示)
-
中值平滑技术(用每个箱的中值代替箱内成员数据)
-
边界值平滑技术(“边界值”指箱中的最大值和最小值,“边界值平滑”指每个值被最近的边界值替换)。
5.数据维度及降维处理
5.1 常见的特征选择方法
-
过滤法
先筛选,再建模。把特征看作 “独立个体”,先根据特征自身的统计属性(比如与目标变量的相关性、方差大小)给特征 “打分”,再按分数筛选出高价值特征,最后用筛选后的特征建模。
-
包裹法
“用模型‘试’出好特征”,把特征选择和 “后续要使用的模型” 绑定,将 “特征子集” 当作 “候选对象”,用模型去 “测试” 不同特征子集的效果(比如模型准确率、误差),最终选择让模型效果最好的特征子集。
-
嵌入法
“建模时‘顺便’选特征”,把特征选择 “嵌入” 到模型训练过程中 —— 模型在学习参数(比如线性回归的系数、决策树的分裂节点)时,会 “自动判断特征的重要性”,训练结束后直接输出 “重要性高” 的特征。
5.2 特征创建方法PCA
主成分分析法PCA:“创造新特征”(特征提取)
主成分分析(Principle Component Analysis,PCA)常用于将数据的属性集转换为新的、更少的、正交的属性集
在主成分分析中,第一主成分具有最大的方差值;第二主成分试图解释数据集中的剩余方差,并且与第一主成分不相关(正交);第三主成分试图解释前两个主成分没有解释的方差,以此类推。
主成分分析的方法论基础为线性代数中的奇异值分解(Singular Value Decomposition)。
在 Python 数据科学编程中,通常采用第三方包 sklearn.decomposition 的 PCA()函数进行主成分分析。PCA 函数的参数如下。
PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None,)
-
n_components:降维后输出的 “新特征(主成分)个数”
- 若设为整数(如
n_components=2):直接指定保留 2 个主成分(适合需要固定维度的场景,比如降维后做可视化,通常选 2 或 3)。 - 若设为小数(如
n_components=0.95):表示保留 “能解释原始数据 95% 方差” 的主成分数量 - 若设为
None(默认值):不主动降维,保留所有主成分(等于没做降维,一般不用)。
- 若设为整数(如
-
copy:是否修改原始数据
copy=True(默认):复制原始数据,处理后原始数据不变copy=False:直接在原始数据上做计算,会修改原始数据 -
whiten:是否白化处理,“白化” 是对生成的主成分做进一步处理,让每个主成分的方差为 1
-
svd_solver:用哪种算法做 SVD
svd_solver='full':完整版 SVD 算法,精准但速度慢(适合小数据集,特征数 < 5000)。svd_solver='randomized':随机 SVD 算法,速度快但精度略低(适合大数据集,特征数多或样本量大)。
-
其他参数一般默认即可
Eg.
比如:用 “年龄、收入” 两个原始特征,通过 PCA 计算出 “主成分 1”(可能是 “年龄 ×0.6 + 收入 ×0.8”)和 “主成分 2”(可能是 “年龄 ×0.8 - 收入 ×0.6”),最终用这 2 个新的主成分替代原始特征,实现降维
6.数据脱敏及其处理
数据脱敏,核心:“让数据‘可用不可识’—— 保留数据的分析、业务价值,同时隐藏或破坏能识别个人 / 敏感主体的信息,避免隐私泄露”
7.数据预处理方法
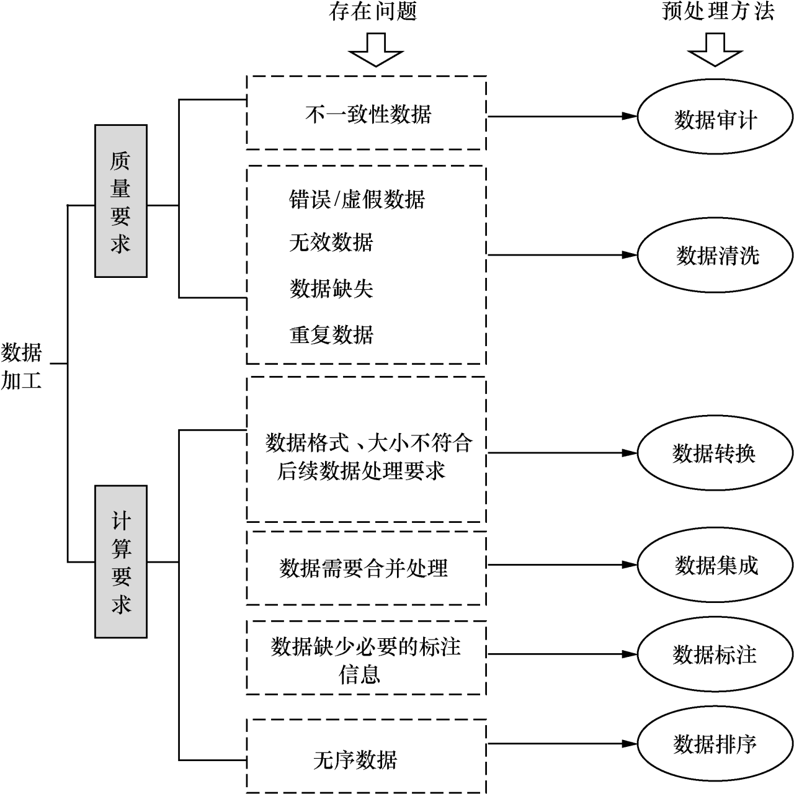
数据加工的主要动机往往来自两个方面:
- 数据质量要求:在数据处理过程中,原始数据中可能存在多种质量问题(如存在缺失值、噪声、错误或虚假数据等),将影响数据处理算法的效率与数据处理结果的准确性。
- 数据计算要求:当原始数据质量没有问题,但不符[合目标算法的要求(如对数据的类型、规模、取值范围、存储位置等要求)时, 我们也需要进行数据加工操作。

