【论文阅读】Gradient Guidance for Diffusion Models:An Optimization Perspective
扩散模型的梯度引导:一种优化视角。
code:https://github.com/yukang123/GGDMOptim
paper:https://proceedings.neurips.cc/paper_files/paper/2024/file/a5059a9a389ccc76da85760ea79490d8-Paper-Conference.pdf
前置知识:
生成扩散模型漫谈(五):一般框架之SDE篇 - 科学空间|Scientific Spaces
笔记|Score-based Generative Models(二)基于 SDE 的模型 | 極東晝寢愛好家
笔记|Score-based Generative Models(一)基础理论 | 極東晝寢愛好家
(99+ 封私信 / 80 条消息) 论文讲解(21):Gradient Guidance for Diffusion Models: An Optimization Perspective - 知乎
讲的都很好,可以看口味自行选择~
太长不看的总结:这篇论文把“在扩散模型采样时加上梯度引导”的经验做法,用优化理论重新解释为一个“正则化优化过程”,并提出了一个新的、理论可证的梯度引导设计(Gloss),既能提升目标函数,又不会破坏生成样本的结构。目前的风格化/personalized做法一般是两种:
-
微调 (fine-tuning):改模型权重(成本高、容易忘掉原分布)。
-
引导 (guidance):在推理时,给反向采样过程加一个“梯度信号”去引导生成。
作者的核心想法:把引导理解为“带正则的优化”。加梯度引导的扩散采样 ≈ 在优化一个带先验约束的目标函数Gloss。
Abstract
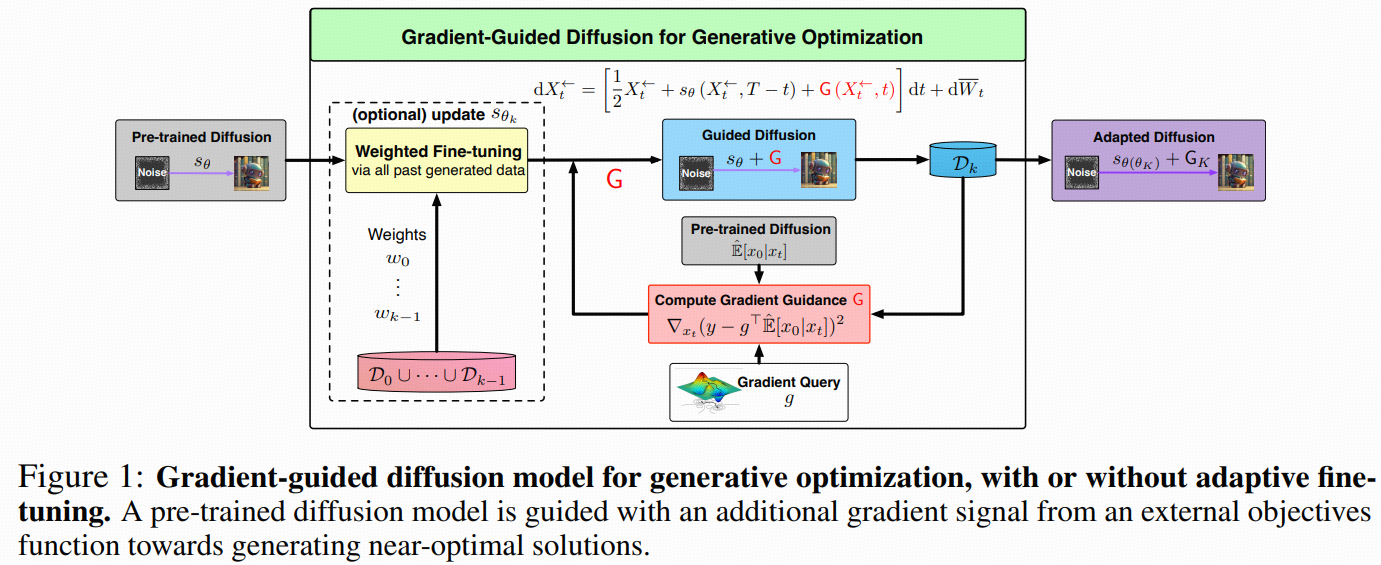
研究“梯度引导”的扩散采样:在不改动预训练扩散模型权重的前提下,向反向采样过程注入来自外部目标函数的梯度信号,使生成样本在保持数据潜在结构的同时,优化目标。作者提出:
-
理论上,梯度引导的扩散采样等价于在预训练数据所施加的“先验正则”下,求解一个正则化优化问题的采样解。这解释了为何仅靠引导无法“无限制地”优化目标——预训练分布构成了硬约束/软正则。
-
设计上,直接对带噪样本加外部目标梯度不可取,会破坏结构;改用一种基于前瞻预测损失(look-ahead / forward prediction loss)的引导,能够利用已学得的 score 信息,并在理论上保持潜在低维子空间结构(定理1)。
-
进一步提出迭代自适应版本:在生成新样本的同时,同时更新“引导”与“score 网络”(类似一阶优化),当目标是凹函数时,期望意义下可达Õ(1/K) 收敛到全局最优(定理3)。
1 Introduction
动机:扩散模型(score-based 生成)强在灵活可控。控制路径主要有两条:微调与推理引导。微调会改权重;引导则在推理期施加方向信号。早期方法有Classifier Guidance与DPS(Diffusion Posterior Sampling,训练无关、直接用损失梯度作引导)。尽管大量实证有效,但缺乏统一的优化理论:
作者聚焦四问:
- 为什么“对带噪样本直接加目标梯度”常常失败?
- 如何在不牺牲样本质量/结构的前提下提升目标?
- 能否证明被引导的样本具备优化性质?
- 适配性的极限是什么(仅靠引导能到哪一步)?
2 Related Works
-
Classifier / Training-free Guidance:从需要时变分类器的引导,到训练无关、以外部损失梯度直接引导的路线;本文与之相似但首次给出严格理论并提出迭代算法。
-
微调(Fine-tuning):RL-based 或直接对 reward 反传,常成本高且易灾难性遗忘;本文首要方案为训练无关引导,并在第6节再讨论自适应微调。
-
扩散理论:既有工作多针对无条件/条件扩散的统计逼近理论;本文新意在于把“梯度引导的采样过程”与“近端/一阶优化步骤”建立等价联系。
3 Preliminaries: Diffusion Models and Guidance
回顾扩散模型的正/反向过程、score 学习(DSM),以及如何在反向采样里加入“引导”(guidance)。
Forward Process

Backward Process

Score Matching

Generation & Guided Generation


目标条件分布与 Bayes 分解


4 A Primer on Gradient Guidance

4.1 Structural Data Distribution with Subspace

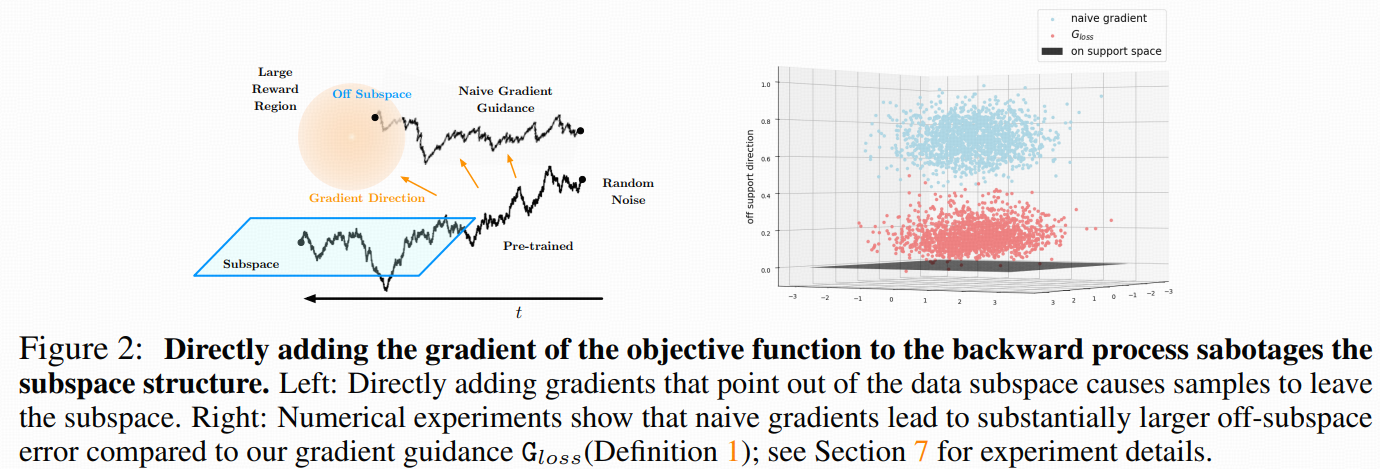
4.2 Naive Gradient Doesn’t Work(朴素梯度失效)

4.3 从条件 score 出发的“结构保持”引导

据此,作者提出通用版的“前瞻损失”引导:

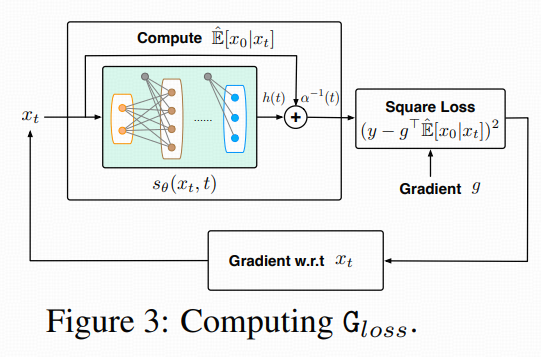
4.4 Gloss的估计与实现


5 Gradient-Guided Diffusion Model as Regularized Optimizer
(把“梯度引导的扩散模型”视为一个带先验正则的优化器)
核心结论(本节要点):
-
迭代式的梯度引导能持续提高目标函数值;
-
预训练扩散模型(通过其 score)在优化视角下等价于对解施加了分布先验的正则化,因此只能收敛到“被正则化的最优”(不是无正则的全局最优)。
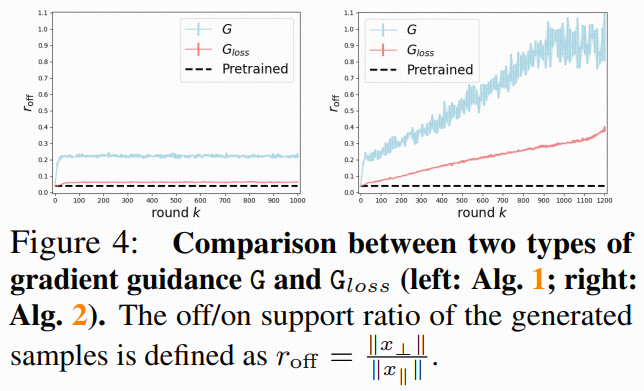
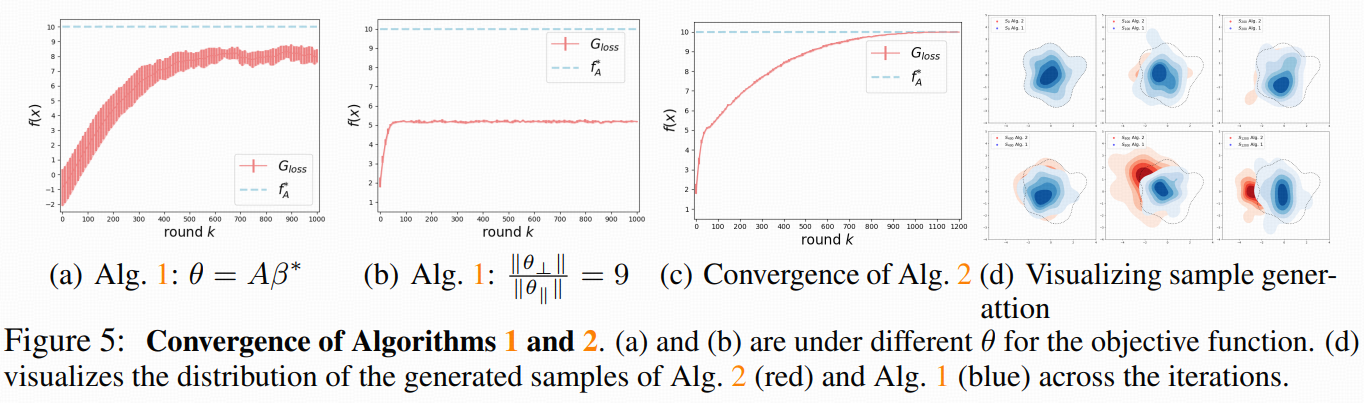
5.1 用预训练 score 的梯度引导生成(Algorithm 1)


5.2 收敛到子空间内的“正则化最优”



6 Gradient-Guided Diffusion with Adaptive Fine-Tuning for Global Optimization
动机:第5节说明了“只有引导”会被预训练先验束缚在正则化解附近。若想要真正的全局最优,就必须动 score(即微调模型),弱化这种束缚。
6.1 带梯度引导的自适应微调(Algorithm 2)


6.2 收敛到无正则的全局最优(在子空间内)



SDE 方程 vs DDPM
总结一句话:
DDPM 是 Score-based SDE 的离散版本;SDE 是 DDPM 的连续极限。