线性代数 - 从方程组到行列式

线性代数 - 从方程组到行列式

flyfish

行列式的英文是determinant ，determinant 的意思是决定因素；决定性因素
说明，对结果、发展起关键作用的人或事物。key determinant（关键决定因素）、major determinant（主要决定因素）、environmental determinants（环境决定因素）

行列式（记为 $\det (A)$ 或 $|A|$）是仅针对方阵（行数 = 列数）定义的一个数值，行列式是一个带符号的数值。

矩阵（线性变换）会对向量做 “缩放、旋转、剪切、翻转” 等操作，而行列式是量化这些操作带来的 “面积 / 体积变化” 和 “定向变化”

简单说就是：行列式的绝对值 = 线性变换的体积 / 面积缩放倍数，符号表示定向。

先不说行列式，先说方程组

方程组

设二元线性方程组为：
$$\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1(1)\\ a_{2}x+b_{2}y=c_2(2)\end{array}$$
其中$a_1,a_2,b_1,b_2$是系数，$c_1,c_2$是常数项，我们的目标是分别消去$y$和$x$，得到只含一个未知数的一元一次方程。

一、消去$y$，得到含$x$的式子

思路：让方程(1)和(2)中$y$的系数相等，再相减抵消$y$

1. 方程(1)两边同时乘以$b_2$（$y$的系数互为对方的系数，确保相乘后$y$系数相同）：
   $$b_2\times (a_{1}x+b_{1}y)=b_2\times c_1$$
   展开得：$$a_1{b}_{2}x+b_1{b}_{2}y=c_1{b}_2(1^{\prime })$$

2. 方程(2)两边同时乘以$b_1$：
   $$b_1\times (a_{2}x+b_{2}y)=b_1\times c_2$$
   展开得：$$a_2{b}_{1}x+b_1{b}_{2}y=c_2{b}_1(2^{\prime })$$

3. 用$(1^{\prime })-(2^{\prime })$（左边减左边，右边减右边，等式仍成立）：
   $$(a_1{b}_{2}x+b_1{b}_{2}y)-(a_2{b}_{1}x+b_1{b}_{2}y)=c_1{b}_2-c_2{b}_1$$

4. 化简左边（抵消$y$项）：
   $$a_1{b}_{2}x-a_2{b}_{1}x+(b_1{b}_{2}y-b_1{b}_{2}y)=(a_1{b}_2-a_2{b}_1)x$$
   右边保持不变：$c_1{b}_2-c_2{b}_1$

5. 最终得到只含$x$的式子：
   $$\boxed{(a_1{b}_2-a_2{b}_1)x=c_1{b}_2-c_2{b}_1}$$

二、消去$x$，得到含$y$的式子

思路：让方程(1)和(2)中$x$的系数相等，再相减抵消$x$

1. 方程(1)两边同时乘以$a_2$：
   $$a_2\times (a_{1}x+b_{1}y)=a_2\times c_1$$
   展开得：$$a_1{a}_{2}x+a_2{b}_{1}y=a_2{c}_1(1^{\prime \prime })$$

2. 方程(2)两边同时乘以$a_1$：
   $$a_1\times (a_{2}x+b_{2}y)=a_1\times c_2$$
   展开得：$$a_1{a}_{2}x+a_1{b}_{2}y=a_1{c}_2(2^{\prime \prime })$$

3. 用$(1^{\prime \prime })-(2^{\prime \prime })$（左边减左边，右边减右边）：
   $$(a_1{a}_{2}x+a_2{b}_{1}y)-(a_1{a}_{2}x+a_1{b}_{2}y)=a_2{c}_1-a_1{c}_2$$

4. 化简左边（抵消$x$项）：
   $$(a_1{a}_{2}x-a_1{a}_{2}x)+a_2{b}_{1}y-a_1{b}_{2}y=(a_2{b}_1-a_1{b}_2)y$$
   右边保持不变：$$a_2{c}_1-a_1{c}_2$$

5. 整理符号（两边同乘$-1$，让系数与消去$y$时一致）：
   $$(a_1{b}_2-a_2{b}_1)y=a_1{c}_2-a_2{c}_1$$
   最终得到只含$y$的式子：
   $$\boxed{(a_1{b}_2-a_2{b}_1)y=a_1{c}_2-a_2{c}_1}$$

两个式子的左边系数完全相同：$a_1{b}_2-a_2{b}_1$——这就是后来定义的二阶行列式$\det (A)$；
当$\det (A)\ne 0$时，才能直接解出$$x=\frac{c_1{b}_2-c_2{b}_1}{\det (A)}$$、$$y=\frac{a_1{c}_2-a_2{c}_1}{\det (A)}$$
消元法的是“减少未知数个数”，而行列式是对消元结果的“符号化简化”。

行列式 determinant

$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$
$\det (A)=\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$

二维矩阵的行列式

从一个2×2矩阵开始。无论你是按行向量还是列向量来书写这些向量，行列式的结果都是一样的。

列向量形式的行列式

例如，按列向量表示时：
$$\left|\begin{array}{cc}a& c\\ b& d\end{array}\right|=ad-bc$$

行向量形式的行列式

若按行向量表示，结果也不会改变：
$$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$$

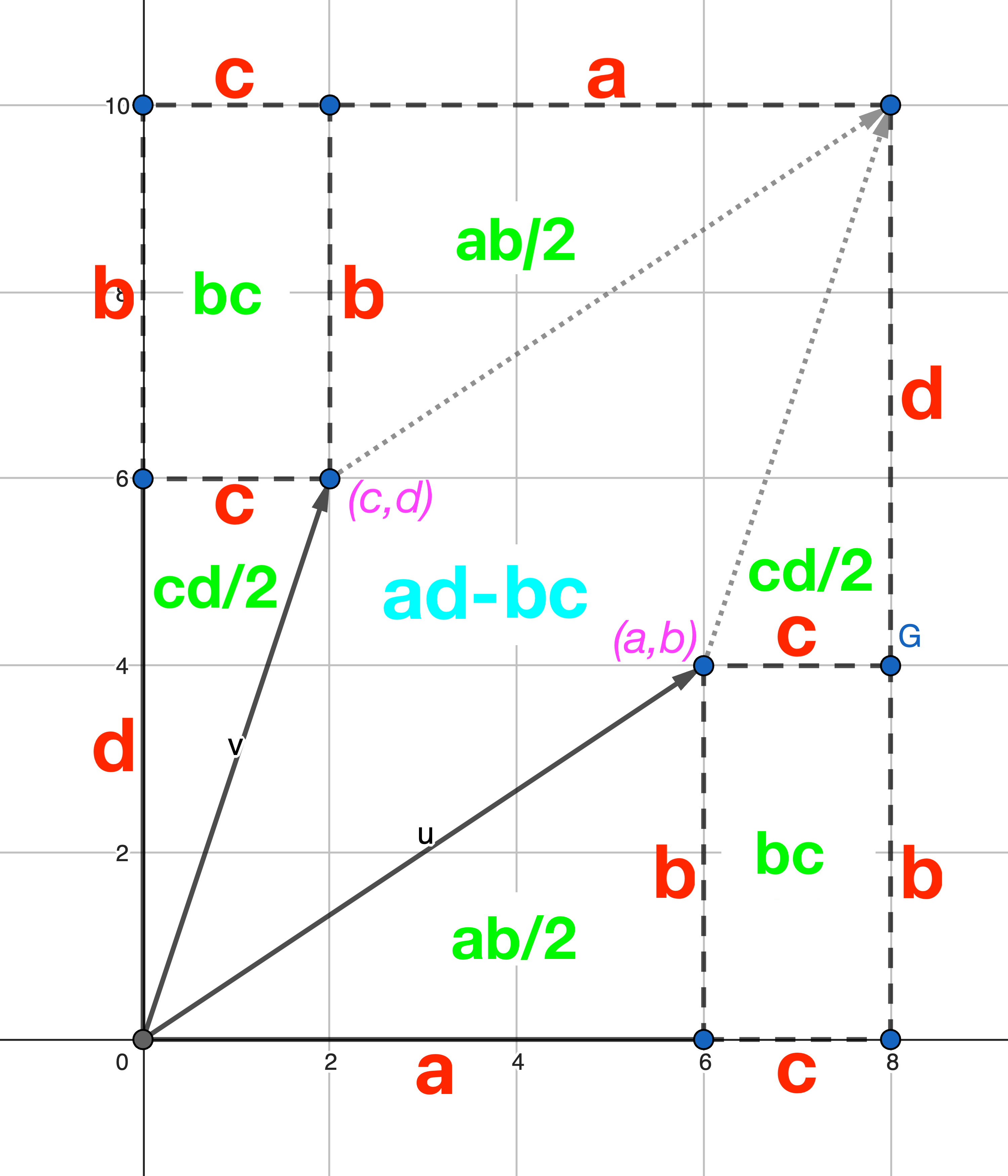
计算方式的直观解释

这个结果实际上是对应平行四边形的面积。因此，无论向量如何书写，面积都不会改变。

可以通过展开式子验证：
$$\begin{array}{rl}\left|\begin{array}{cc}a& c\\ b& d\end{array}\right|& =(a+c)(b+d)-ab-cd-2bc\\ & =ab+ad+cb+dc-ab-cd-2bc\\ & =ad-bc\end{array}$$

交换列对行列式的影响

若交换两列，行列式的值会改变符号。例如：
$$\left|\begin{array}{cc}c& a\\ d& b\end{array}\right|=cb-ad=-(ad-bc)=-\left|\begin{array}{cc}a& c\\ b& d\end{array}\right|$$

例1

已知矩阵$C=\left[\begin{array}{cc}-9& -2\\ 3& -1\end{array}\right]$，求$|C|$。
解答：我们需要求上述2×2矩阵的行列式。使用公式计算行列式，过程如下：
$$\det (C)=|C|=\left|\begin{array}{cc}-9& -2\\ 3& -1\end{array}\right|=(-9)\times (-1)-(-2)\times 3=9+6=15$$

例2

已知$\left|\begin{array}{cc}1& x\\ 8& 2\end{array}\right|=34$，求$x$。
解答：已知行列式值，需要求元素$x$。将其代入公式并求解$x$：
$$\left|\begin{array}{cc}1& x\\ 8& 2\end{array}\right|=34⟹(1)\times (2)-(x)\times (8)=34⟹2-8x=34⟹-8x=34-2⟹-8x=32⟹x=-4$$

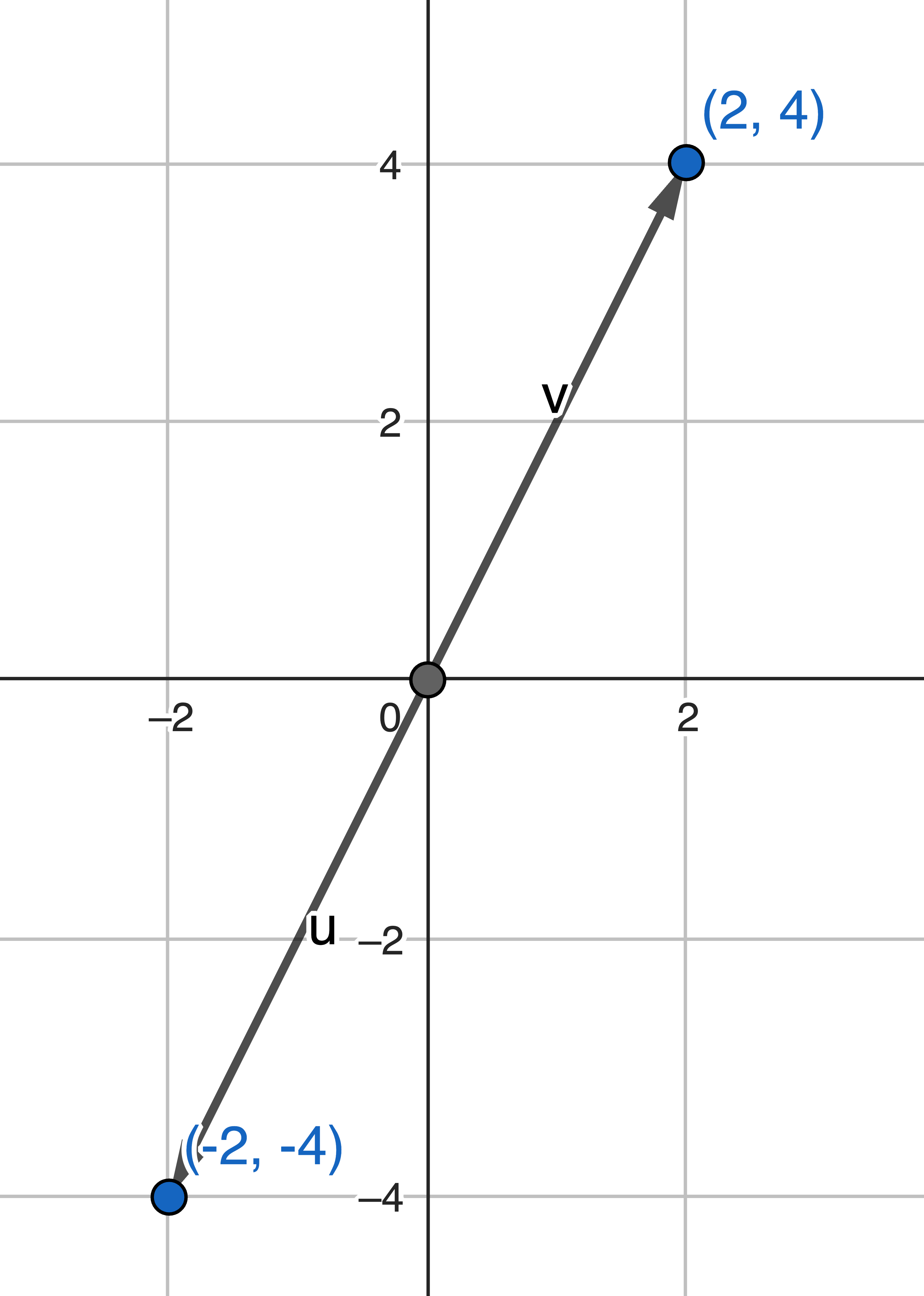
可视化

$$\det (\left[\begin{array}{cc}4& 2\\ 2& 4\end{array}\right])=4\ast 4-2\ast 2=12$$

$$\det (\left[\begin{array}{cc}2& -2\\ 4& -4\end{array}\right])=2\ast (-4)-4\ast (-2)=0$$