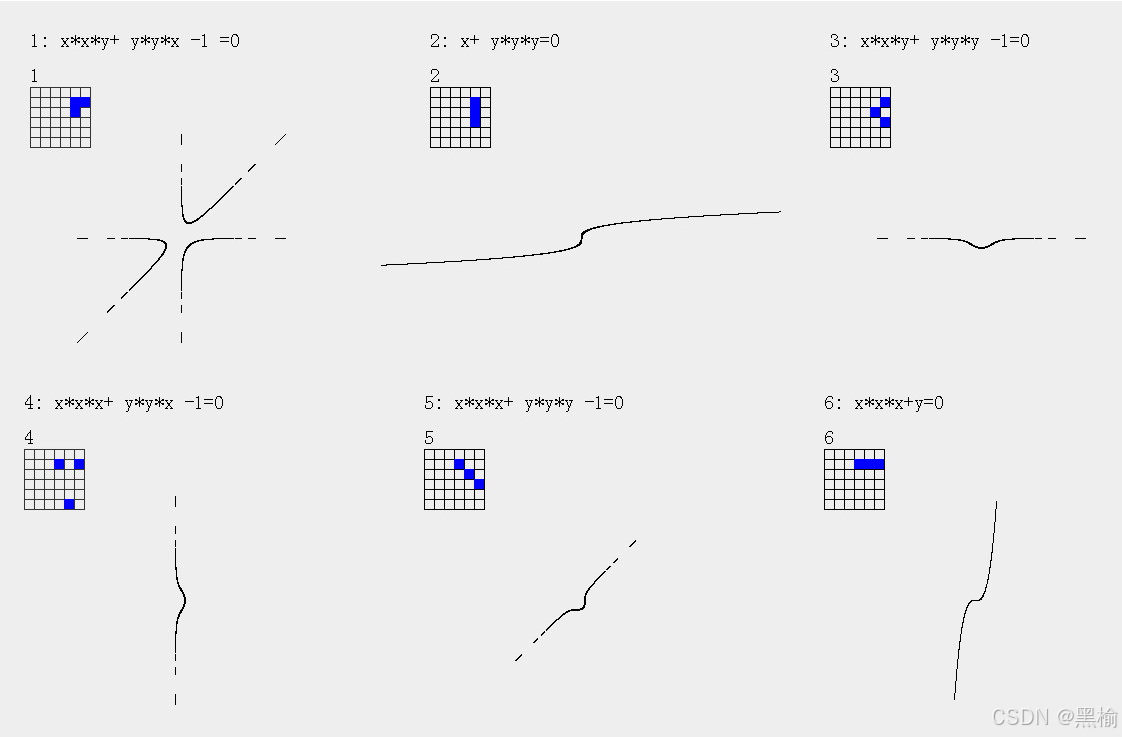
统计3次函数3a6的种类和数量

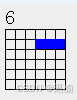
3a6这个结构x方向有3次，y方向有1次。因此其对称性可以用方程x*x*x+y=0表示。

这次计算一个函数最高次为x*x*x时可能有多少种变化。

最高次为x*x*x,因此可能的二次项有x*x，x*y，y*y，一次项有x，

可能有16种排列组合，对应的方程分别为

	x*x*x	x*x	x*y	y*y	x	y
1	1					1		1	x*x*x+ y=0
2	1	1				1		2	x*x*x+ x*x+ y=0
3	1		1			1		3	x*x*x+ x*y+ y=0
4	1			1		1		4	x*x*x+ y*y+ y=0
5	1				1	1		5	x*x*x+ x+ y=0
6	1	1	1			1		6	x*x*x+ x*x+ x*y+ y=0
7	1	1		1		1		7	x*x*x+ x*x+ y*y+ y=0
8	1	1			1	1		8	x*x*x+ x*x+ x+ y=0
9	1		1	1		1		9	x*x*x+ x*y+ y*y+ y=0
10	1		1		1	1		10	x*x*x+ x*y+ x+ y=0
11	1			1	1	1		11	x*x*x+ y*y+ x+ y=0
12	1	1	1	1		1		12	x*x*x+ x*x+ x*y+ y*y+ y=0
13	1	1	1		1	1		13	x*x*x+ x*x+ x*y+ x+ y=0
14	1	1		1	1	1		14	x*x*x+ x*x+ y*y+ x+ y=0
15	1		1	1	1	1		15	x*x*x+ x*y+ y*y+ x+ y=0
16	1	1	1	1	1	1		16	x*x*x+ x*x+ x*y+ y*y+ x+ y=0

把这16个方程画成图为

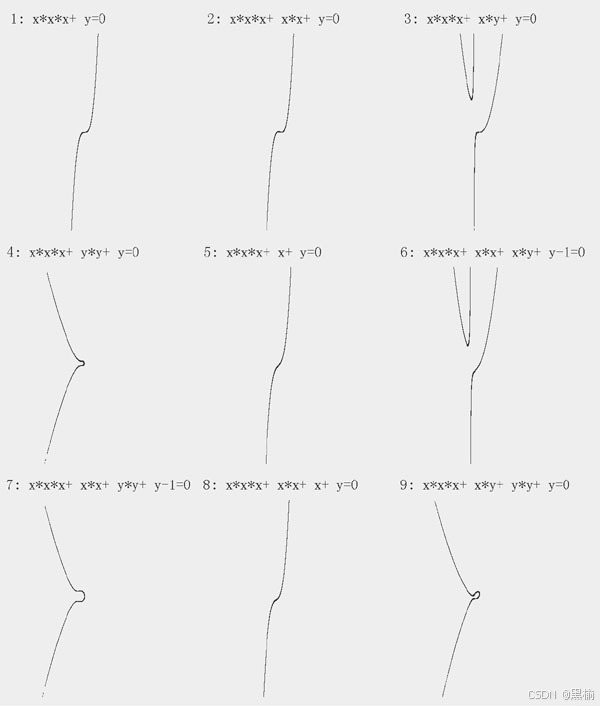
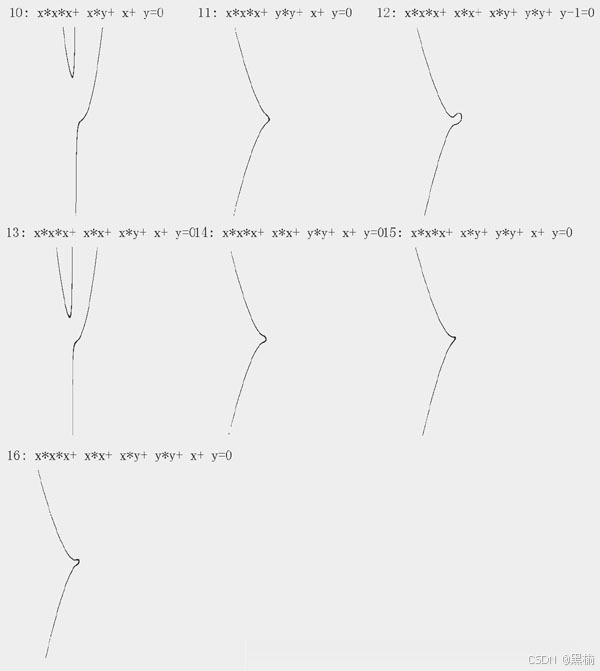
这16张图可以被分成4组

1	x*x*x+y=0	4	x*x*x+ y*y+ y=0
2	x*x*x+x*x+y=0	7	x*x*x+ x*x+ y*y+ y=0
5	x*x*x+ x+ y=0	11	x*x*x+ y*y+ x+ y=0
8	x*x*x+ x*x+ x+ y=0	14	x*x*x+ x*x+ y*y+ x+ y=0
3	x*x*x+ x*y+ y=0	9	x*x*x+ x*y+ y*y+ y=0
6	x*x*x+ x*x+ x*y+ y=0	12	x*x*x+ x*x+ x*y+ y*y+ y=0
10	x*x*x+ x*y+ x+ y=0	15	x*x*x+ x*y+ y*y+ x+ y=0
13	x*x*x+ x*x+ x*y+ x+ y=0	16	x*x*x+ x*x+ x*y+ y*y+ x+ y=0

第一组：1，2，5，8

第二组：4，7，11，14

第三组：3，6，10，13

第四组：9，12，15，16

比较第一组

1	x*x*x+y=0
2	x*x*x+x*x+y=0
5	x*x*x+ x+ y=0
8	x*x*x+ x*x+ x+ y=0

因为一次项x和二次项x*x都从属于3次项x*x*x，所以可以理解为x和x*x这种对称性在x*x*x中已经表达过了，因此重复的一次项和二次项并未给图像带来新的对称性，因此2，5，8这4条线的内在对称性和1是一致的。

所以这16条线只体现了4种对称性，因此可以被分成4组

1	x*x*x+y=0
3	x*x*x+ x*y+ y=0
4	x*x*x+ y*y+ y=0
9	x*x*x+ x*y+ y*y+ y=0

因此上次得到的3ax的6个函数可以被继续化简

3a1=	( x*x + 2*x*x*y )/3 + (2*y*y*x +  y*y)/3
3a2=	x+y*y*y
3a3=	(x*x+ 2*x*x*y)/3 + (y*y*y + 2*y*y*y)/3
3a4=	(2*x*x*x + x*x*x)/3 + (2*y*y*x +y*y)/3
3a5=	x*x*x+y*y*y
3a6=	x*x*x+y

因为x*x从属于x*x*y，而系数只表达一种放缩，因此3a1可以化简为

3a1=	x*x*y + y*y*x

所有6项化简得到

3a1=	x*x*y + y*y*x
3a2=	x+y*y*y
3a3=	x*x*y + y*y*y
3a4=	x*x*x + y*y*x
3a5=	x*x*x+y*y*y
3a6=	x*x*x+y