简单的损失函数与复杂的对齐

实际上，损失函数或奖励函数只是我们真正想要的东西的简化。它们之所以“粗糙”，仅仅是因为它们必须将复杂的目标压缩成模型可以进行数学优化的形式。

为什么目标总是过于简单？损失函数 L(θ) 通常只能捕捉到一个可衡量的指标：准确率、奖励、与目标的距离。但人类的目标是多维的。当我们只选择一个指标时，不可避免地会扭曲其他指标。这就是为什么目标对齐通常意味着修改 L，使其包含一些额外的项来近似我们关心的其他值。

对齐是目标函数的数学混合。在实践中，“对齐”损失是各个部分目标函数的加权和：

L_{total}(\theta) = \lambda_1 L_{main}(\theta) • \lambda_2 L_\text{safety}(\theta) • \lambda_3 L_\text{fairness}(\theta) • \lambda_4 L_\text{style}(\theta) …

每个 \lambda_i 都定义了我们对该属性的重视程度。如果某个项的权重过高，模型就会过度拟合；如果权重过低，该项则会消失。调整这些 \lambda 值是对齐的实用艺术。

 “混合”会对优化产生影响，添加新的对齐目标会改变损失函数的形态。想象一下，我们从一个光滑的碗状损失函数 L_\text{main} 开始。每增加一个项，它都会略微扭曲，使其向更安全或更公平的解倾斜。优化器（梯度下降）仍然遵循以下公式：

 

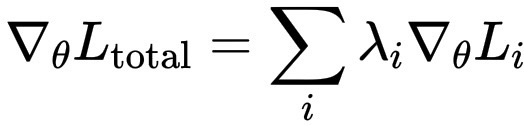
\nabla_\theta L_\text{total} = \sum_i \lambda_i \nabla_\theta L_i

因此，每个目标函数实际上都会根据其权重对参数产生相应的影响。

由于梯度是向量和，不同的目标函数在参数空间中可能指向相反的方向。这就是为什么对齐如此微妙：过分强调安全性，会降低实用性；过分强调实用性，则会损害安全性。完美的对齐是所有这些因素达到平衡的平衡点。基本目标很简单，而对齐的过程就是不断叠加其他目标，直到模型的优化图景开始反映出设计者意图的真正复杂性。

---

为什么复杂的损失函数会导致早期训练不稳定？

在训练初期，模型的参数是随机的，梯度也存在噪声。如果一开始就添加过多的目标函数，尤其是那些方向不一致的目标函数，组合损失函数的曲面将不再是清晰的凸“碗状”，而是变得粗糙，充满局部最小值和鞍点。

数学上来说，如果

L_{total}(\theta)= \sum_i \lambda_i L_i(\theta),

并且梯度 \nabla_\theta L_i 在早期指向不一致的方向，那么它们的和可能会振荡或相互抵消，导致优化速度变慢或发散。这就是为什么预训练通常只关注一个简​​单且形状良好的目标函数，例如最小化交叉熵。模型首先需要学习世界的基本“结构”，才能处理更微妙的人类价值观。

一旦实现了基础目标，模型掌握了语言、逻辑或感知，我们就可以安全地添加对齐项。

在这个阶段，参数已经接近损失函数的平滑区域，在这个区域内，一些小的附加因素（例如安全或公平性项）可以温和地重塑行为，而不会破坏核心能力。

换句话说，在早期阶段，模型脆弱，需要简洁性的单一目标。后期阶段，模型稳定，可以容忍复杂性，可以进行多目标对齐。

这就像先学习走路，再学习礼仪。如果你试图一次性纠正所有可能的错误，比如姿势、步伐、礼仪，孩子会不知所措，反而会僵住不动。但一旦行走成为一种自然而然的习惯，你就可以通过更小、更持续的调整来完善行为。