【代数学】置换群的正规子群与猜拳游戏

猜拳策略

在猜拳游戏中，每个置换 $\sigma \in S_3$ 可以解释为一个策略函数：当玩家1出动作 $A\in X$ 时，玩家2出 $\sigma (A)$。在人 v.s. 人环境下上述策略属于作弊，但是部分电子游戏就是机器接收到人类的猜拳结果后才给出相应结果的，为了提高玩家的兴趣而设计的，并非必赢策略，而是动态可找规律策略，一旦学得策略可在本时段一直赢，换时段时需要重新学习策略。 输赢规则固定为：

• 石头赢剪刀（石 > 刀）
• 剪刀赢布（刀 > 布）
• 布赢石头（布 > 石）

因此有以下6种策略映射，注意

1. ${\sigma }_1(石，刀，布)=(石,刀,布)$ 可视为必平策略
2. ${\sigma }_2(石，刀，布)=(刀,布,石)$ 可视为必赢策略
3. ${\sigma }_3(石，刀，布)=(布,石,刀)$ 可视为必输策略
4. ${\sigma }_4(石，刀，布)=(石,布,刀)$ 可视为平石策略
5. ${\sigma }_5(石，刀，布)=(布,刀,石)$ 可视为平刀策略
6. ${\sigma }_6(石，刀，布)=(刀,石,布)$ 可视为平布策略

机器策略构成群

观察映射的复合
${\sigma }_1\circ {\sigma }_i={\sigma }_i\circ {\sigma }_1={\sigma }_i$, 因此 ${\sigma }_1$ 就是单位元。
而
${\sigma }_1^{-1}={\sigma }_1$
${\sigma }_2^{-1}={\sigma }_3$
${\sigma }_3^{-1}={\sigma }_2$
${\sigma }_4^{-1}={\sigma }_4$
${\sigma }_5^{-1}={\sigma }_5$
${\sigma }_6^{-1}={\sigma }_6$

因此每个策略都有其逆元。 结合律显然，因此 S3={σ1,σ2,σ3,σ4,σ5,σ6}S_3=\{\sigma_1,\sigma_2,\sigma_3,\sigma_4,\sigma_5,\sigma_6\}S3​={σ1​,σ2​,σ3​,σ4​,σ5​,σ6​} 构成群。

$S_3$ 正规子群

给定 $S$ 的子群 $A$，如果任意 ${\sigma }_i\in S$ 满足 ${\sigma }_{i}A=A{\sigma }_i$, 则称 $A$ 为 $S$ 的正规子群。

针对 $S_3$ 而言 其子群 A3={σ1,σ2,σ3}A_3=\{\sigma_1,\sigma_2,\sigma_3\}A3​={σ1​,σ2​,σ3​} 就是一个正规子群， 恰好是必平，必胜，必输策略构成的。 验证 $A_3$ 是否为 $S_3$ 的正规子群，我们让 python 来验证。

import numpy as np
import numpy.linalg as ladef pmt_oe(a):# 判断元素 a 是奇置换还是偶置换, 如果是奇置换输出-1, 如果是偶置换输出1m,n=a.shapes=1for i in range(n-1):for j in range(i,n):if a[1,i]> a[1,j]:s=-sc=a[1,i]a[1,i]=a[1,j]a[1,j]=c                return(s)def mult_pmt(a,b):# 置换群的乘法运算m,n=b.shapeif len(a) == len(b):c=np.array(a)for j in range(n):c[0,j]=jd=int(b[1,j])c[1,j]=a[1,d]else: print('error: length a does not equal to length b')return(c)n=3
print(pmt_oe(np.array([[0,1,2],[0,1,2]])))
print(pmt_oe(np.array([[0,1,2],[1,2,0]])))
print(pmt_oe(np.array([[0,1,2],[2,0,1]])))
def L_coset(S,a):  # 计算左陪集 aSlth=len(S)C=[[]]*lthfor j in range(lth):C[j]=mult_pmt(a,S[j])return(C)def R_coset(S,a):  # 计算右陪集 Salth=len(S)C=[[]]*lthfor j in range(lth):C[j]=mult_pmt(S[j],a)return(C)def ele_grp(S,a): # 判断元素a是否在群S中lth=len(S)y=Falsefor i in range(lth):if la.norm(a-S[i],ord='fro')==0:y=Truereturn(y)def is_equal(S1,S2): # 判断集合S1与S2是否相同if not(len(S1)==len(S2)):return(False)else:s=Truelth=len(S1)for i in range(lth):if not ele_grp(S2,S1[i]):s=Falseif not ele_grp(S1,S2[i]):s=Falsereturn(s)def is_abel_vrt(S,G):# 判断 S是否是G的正规子群rt=Truelth=len(G)for i in range(lth):cL=L_coset(S,G[i])cR=R_coset(S,G[i])if not is_equal(cL,cR):rt=Falsereturn(rt)
def quot_grp(S,G):  # 求置换群G的模掉正规子群S的商群lth=len(G)lsh=len(S)qt=[G[0]]for i in range(lth):lqh=len(qt)GL=L_coset(S,G[i])idx=1for j in range(lqh):            qL=L_coset(S,qt[j])if is_equal(GL,qL):idx=0if idx:qt=qt+[G[i]]return(qt)

案例

def pmt_grp(arr,n):v=np.ones([2,n])v[0,:]=np.arange(0,n,1)v[1,:]=np.arange(0,n,1)lth=len(arr)for i in range(lth):if i==lth-1:a=arr[i]b=arr[0]            v[1,a]=belse:                a=arr[i]b=arr[i+1]v[1,a]=b       return(v)
n=3
a0=pmt_grp(np.array([0]),n) 
a1=pmt_grp(np.array([0,1]),n) 
a2=pmt_grp(np.array([0,2]),n) 
a3=pmt_grp(np.array([1,2]),n) 
a4=pmt_grp(np.array([0,1,2]),n) 
a5=pmt_grp(np.array([0,2,1]),n) 
S3=[a0,a1,a2,a3,a4,a5]
S2=[a0,a1]
A3=[a0,a4,a5]CL=L_coset(S2,a2)
CR=R_coset(S2,a2)
print(CL)
print(CR)
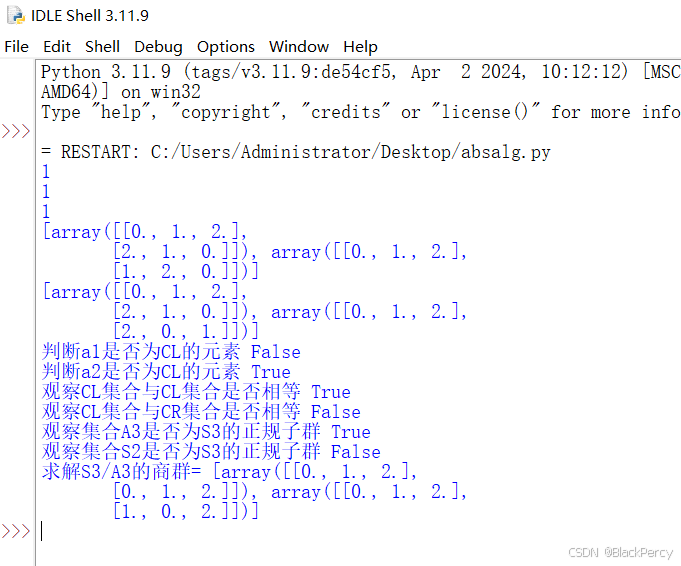
print('判断a1是否为CL的元素',ele_grp(CL, a1))
print('判断a2是否为CL的元素',ele_grp(CL, a2))print('观察CL集合与CL集合是否相等', is_equal(CL,CL))
print('观察CL集合与CR集合是否相等', is_equal(CL,CR))
print('观察集合A3是否为S3的正规子群', is_abel_vrt(A3,S3))
print('观察集合S2是否为S3的正规子群', is_abel_vrt(S2,S3))print('求解S3/A3的商群=',quot_grp(A3,S3))