数学分析简明教程——总练习题1(未完)
3直接带入,略
6,7作图题,略
【Easy】1.设,证明:
对于(1)当a>b时,
当a<=b时,
因此(1)得证,(2)同理可得
【Easy】2.设f和g都是D上的初等函数,定义
试问M(x),m(x)是否是初等函数
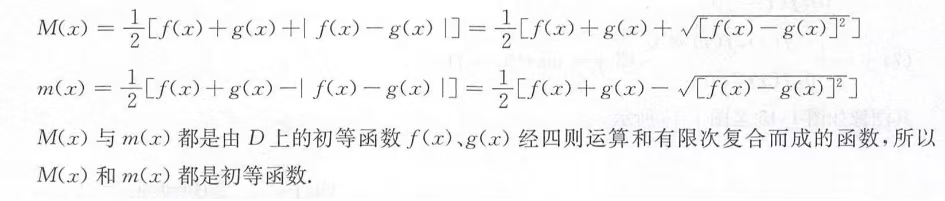
【Easy】4.已知,求f(x).
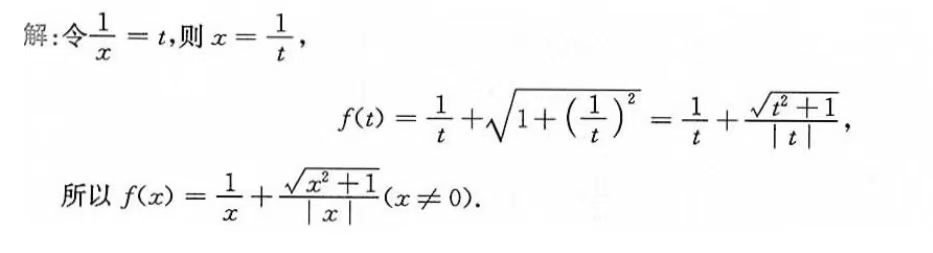
这里注意t要带上绝对值
【Easy】5.
满三人多加一个名额,可以加2把3补到5,这样大于等于3的数都可以当作5算
故对于第一题
第二题同理
【Easy】8.设f,g,h为增函数,满足
证明:

3直接带入,略
6,7作图题,略
【Easy】1.设,证明:
对于(1)当a>b时,
当a<=b时,
因此(1)得证,(2)同理可得
【Easy】2.设f和g都是D上的初等函数,定义
试问M(x),m(x)是否是初等函数
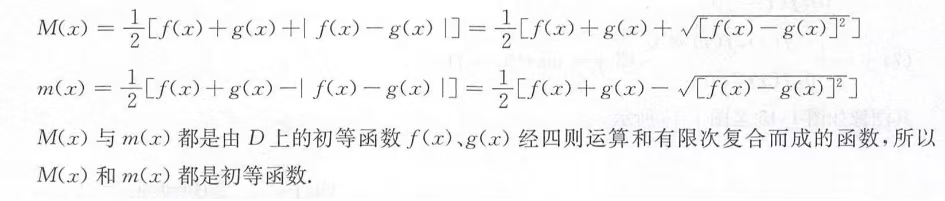
【Easy】4.已知,求f(x).
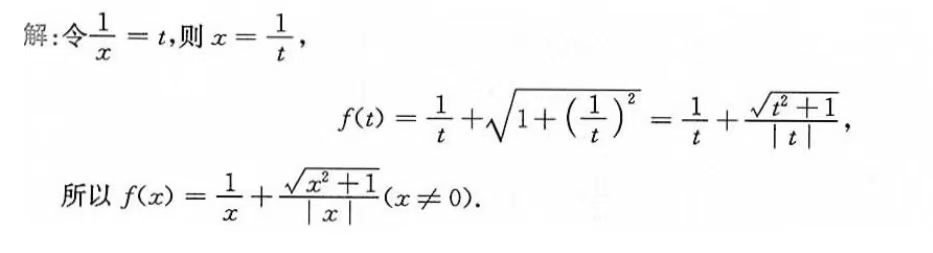
这里注意t要带上绝对值
【Easy】5.
满三人多加一个名额,可以加2把3补到5,这样大于等于3的数都可以当作5算
故对于第一题
第二题同理
【Easy】8.设f,g,h为增函数,满足
证明:
