【递归、回溯、搜索】专题六:记忆化搜索
目录
一*、斐波那契数
二、不同路径
三、最长递增子序列
四、猜数字大小II
五、矩阵中的最长递增路径
一*、斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
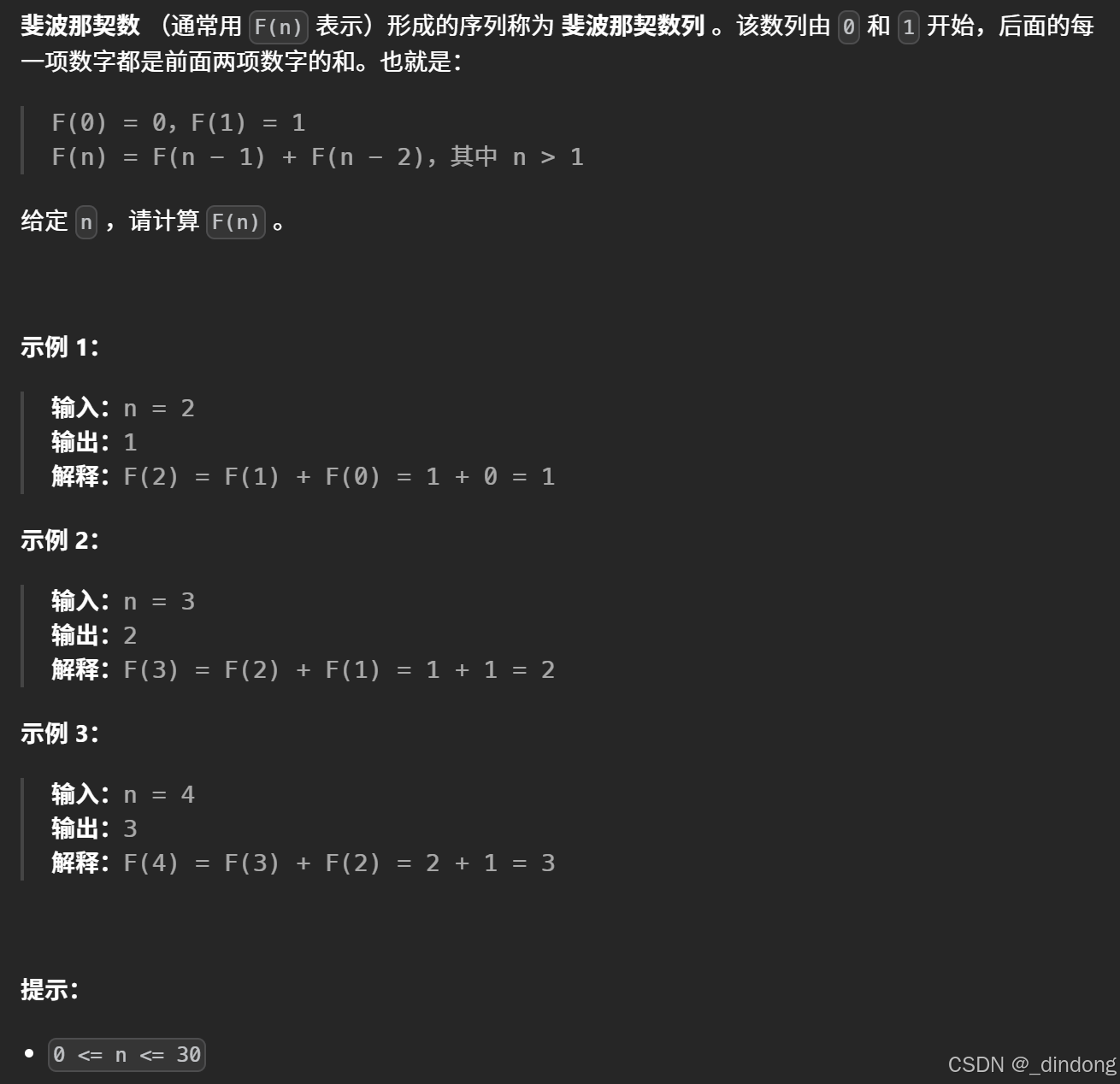
有些题记忆化搜索与动规等同,就像这题
解法一:递归
思路如下:
递归,O 2^n,画出递归展开树,我们发现,总会有些重复计算,比如n=5时d(3)就求了很多次,如果n越大,那么重复的计算会非常多。那么我们是不是可以用一个备忘录储存一下计算过的值,如果后边要拿这个数,那么就能直接拿到不用再递归计算了,从而将时间复杂度从指数级别降到线性级别这就是记忆化搜索。
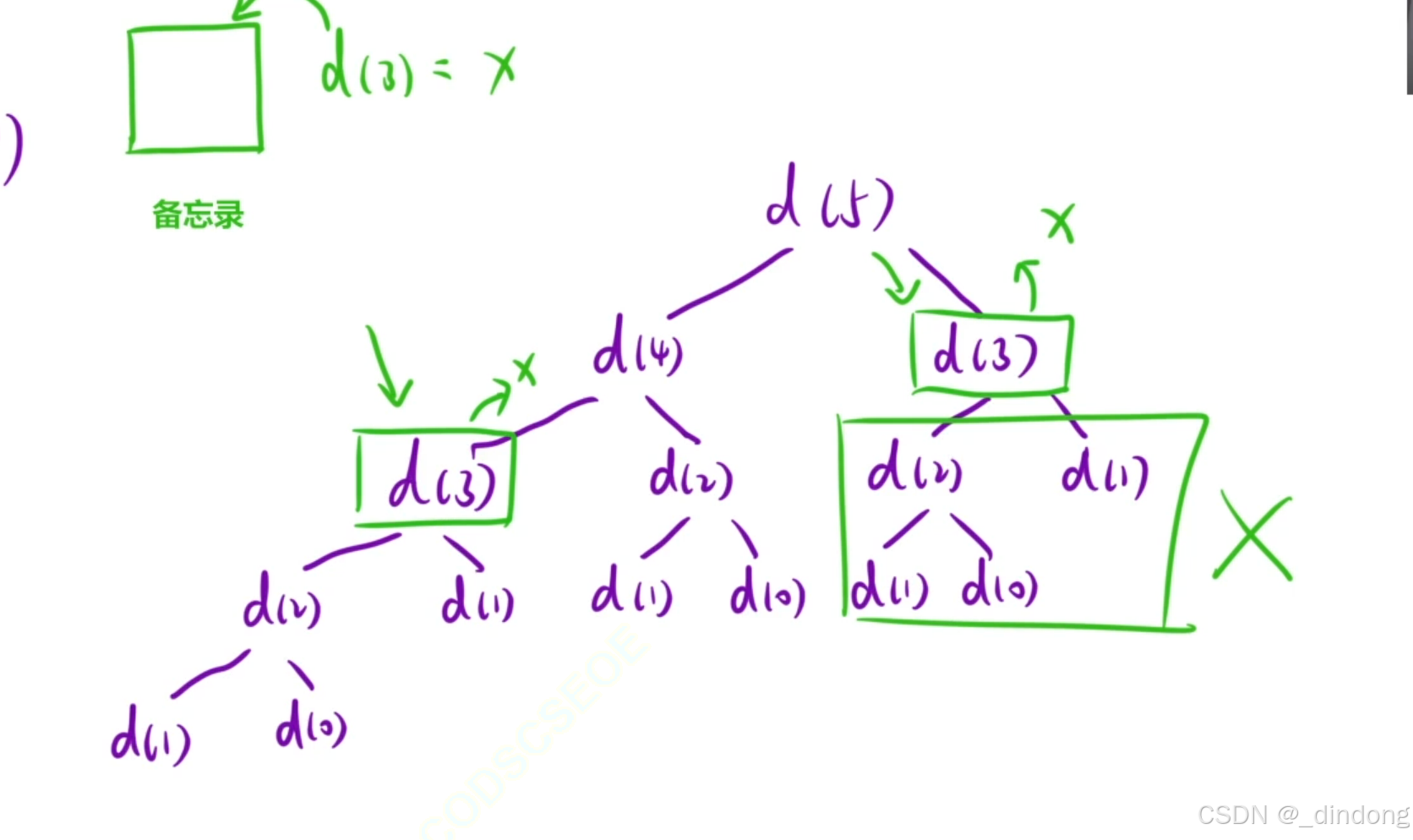
递归代码如下:
class Solution {
public:int fib(int n) {return dfs(n);}int dfs(int n){if(n==0||n==1)return n;return dfs(n-1)+dfs(n-2);}
};解法二:记忆化搜索(避免重复运算,复杂度降低到线性)
记忆化搜索(备忘录递归)(自顶向下)O(n)
备忘录具体如何实现?
我们需要建立可变参数与计算值的映射关系,所以需要哈希表的思想
而我们本题创建一个数组就可以了。

记忆化搜索实现如下:
class Solution {//刚需31,不能用={-1}初始化,全局变量这样处理,只会第一个是-1int memo[31];
public:int fib(int n) {memset(memo,-1,sizeof memo);return dfs(n);}int dfs(int n){//往备忘录看一眼if(memo[n]!=-1){return memo[n];}//和递归终点初始化一样,往备忘录塞数if(n==0||n==1){memo[n]=n;return memo[n];}//往备忘录塞数memo[n]=dfs(n-1)+dfs(n-2);return memo[n];}
};解法三:动态规划(自下上顶),常规的动态规划和记忆化搜搜本质差别不大。
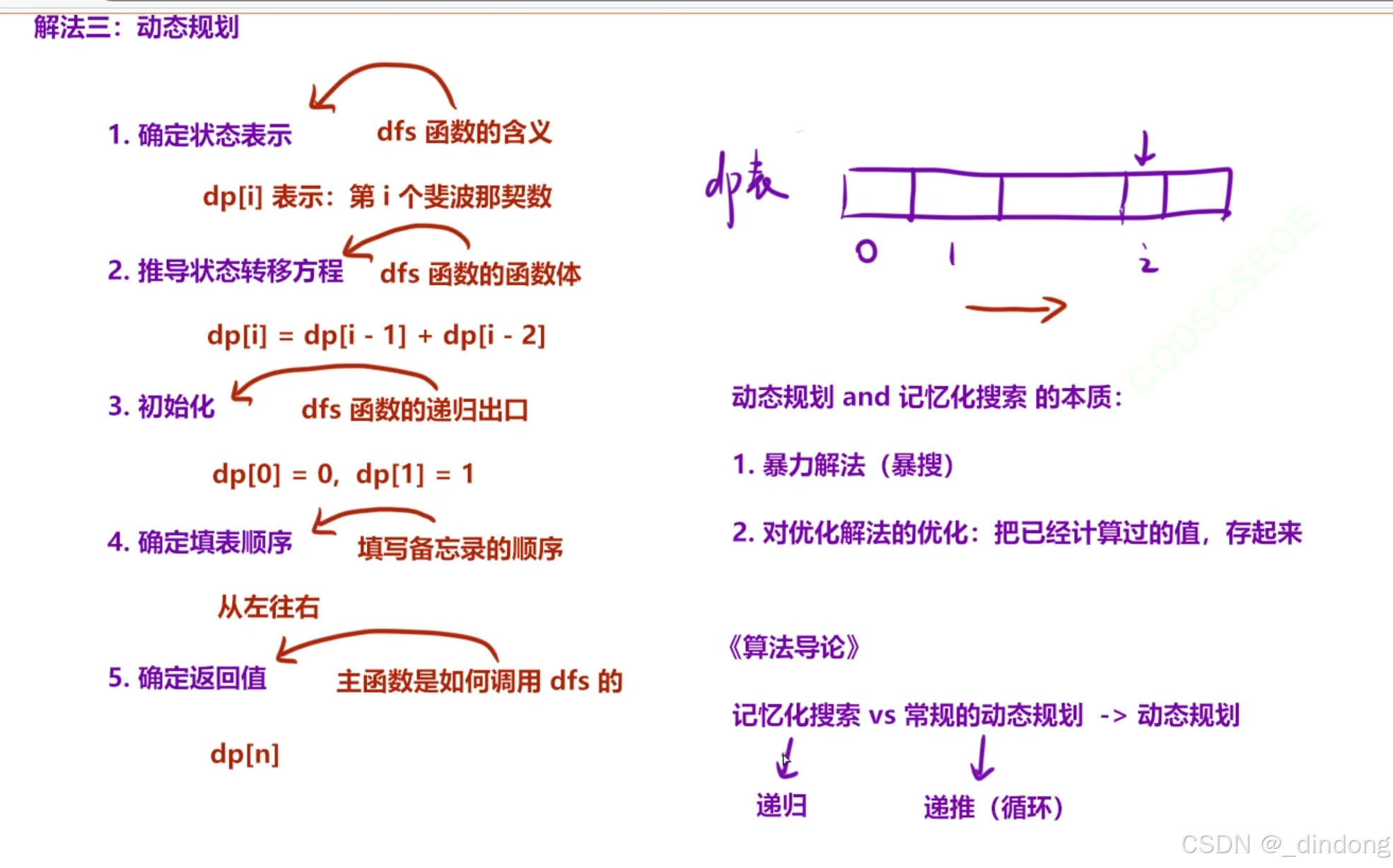
dp实现如下:
class Solution {int dp[31];
public:int fib(int n) {dp[0]=0,dp[1]=1;for(int i=2;i<=n;++i){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
};二、不同路径
62. 不同路径 - 力扣(LeetCode)

思路如下:
纯递归会超时,优化为记忆化搜索
注意该题相当于从1,1的位置出发
到达某点的方法,等于到上面那个点方法+到左边那个点方法之和
代码实现如下:
解法一:记忆化搜索
class Solution {int memo[101][101];
public:int uniquePaths(int m, int n) {return dfs(m, n);}int dfs(int m, int n) {if (memo[m][n] != 0) {return memo[m][n];}//上,左边界全部处理为0if (m == 0 || n == 0){return memo[m][n];}if (m == 1 && n == 1) {memo[m][n] = 1;return memo[m][n];}memo[m][n] = dfs(m - 1, n) + dfs(m, n - 1);return memo[m][n];}
};解法二:dp,还是动规代码更好看
class Solution {int dp[101][101];
public:int uniquePaths(int m, int n) {dp[1][1]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(i==1&&j==1)continue;dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};三、最长递增子序列
300. 最长递增子序列 - 力扣(LeetCode)
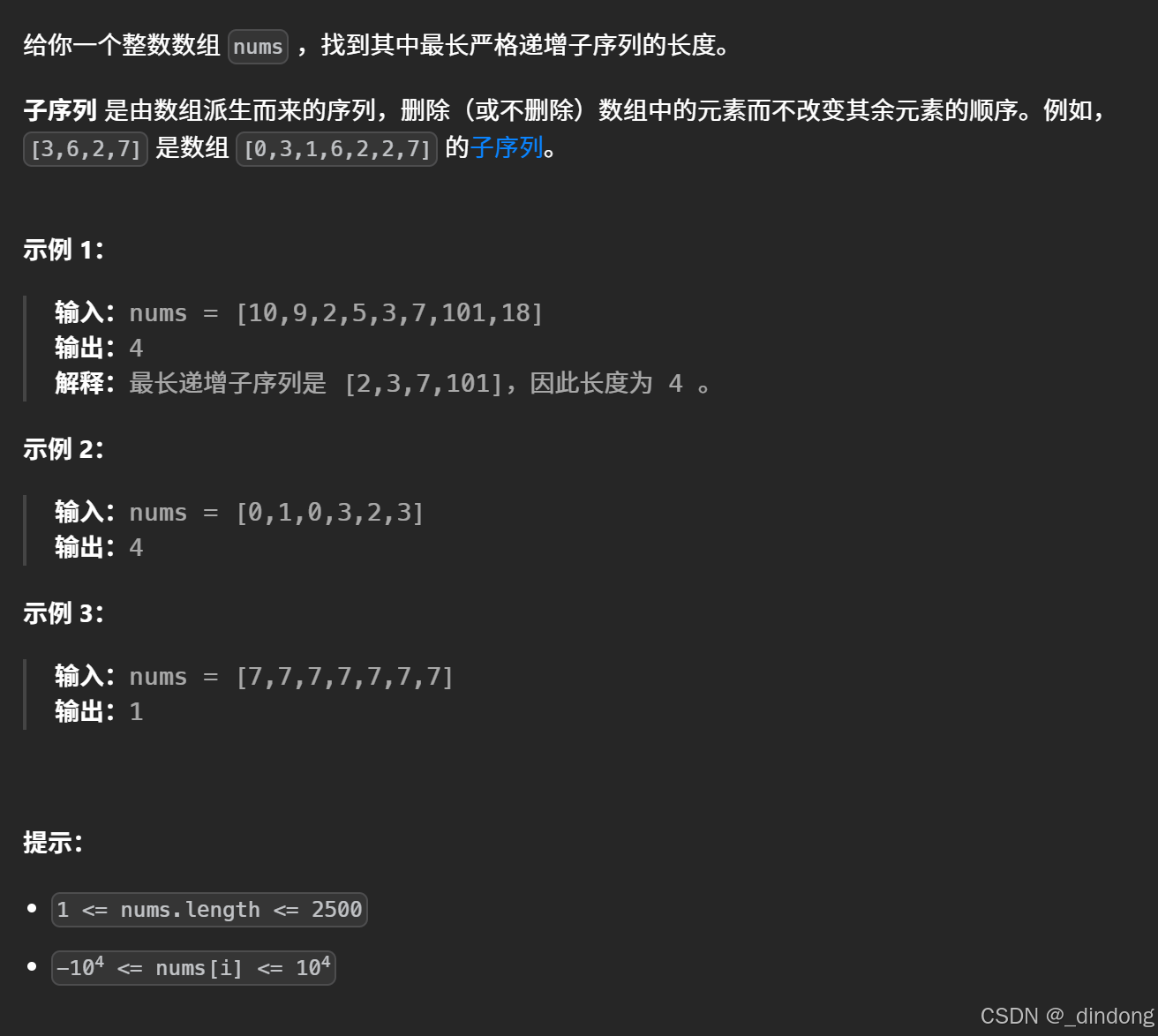
先看看暴力如何做
思考递归每一层都在干什么
1.暴力就是从每一个元素为起点,后边遇到数字变大的就更新path,递归每层我们都要创建一个path,然后计算这个位置往后的最大的,返回这个path
搞清每次都在干什么就很好写了,不过该代码会超时,因为是n叉树,复杂度近乎于n^n,非常高
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int ret=0;for(int i=0;i<nums.size();++i){ret=max(ret,dfs(nums,i));}return ret;}int dfs(vector<int>& nums,int pos){int path=1;for(int i=pos+1;i<nums.size();++i){if(nums[i]>nums[pos]){//不能path+=dfs(nums,i) or path=dfs(nums,i)+1//因为这里for循环遍历在暴搜这个位置往后的可能最大值,每次需要比较path=max(path,dfs(nums,i)+1);}}return path;}
};2.记忆化优化,因为后边遇到更大数字要更新path,如果memo里有这个数字,那么我们只需要加上这个最大数字位置(可能会有重复)往后最大的递增子序列长度就行。创建一个备忘录,dfs函数开头先检查这个位置记录了没有,有返回,没有进入dfs内部,计算完这个位置后在备忘录记录。
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> memo(nums.size());int ret=0;for(int i=0;i<nums.size();++i){ret=max(ret,dfs(nums,i,memo));}return ret;}int dfs(vector<int>& nums,int pos,vector<int>& memo){//查找备忘录,看一下这个位置有没有记录if(memo[pos]!=0)return memo[pos];int path=1;for(int i=pos+1;i<nums.size();++i){if(nums[i]>nums[pos]){//不能path+=dfs(nums,i) or path=dfs(nums,i)+1//因为这里for循环遍历在暴搜这个位置往后的可能最大值,每次需要比较path=max(path,dfs(nums,i,memo)+1);}}memo[pos]=path;return path;}
};3.dp,动规后续会出一个专栏专门讲解
因为我求一个位置最长子序列,都要知道这个位置往后的情况,那么我们dp就得从后往前更新,因为往后才是最底的那个部分
class Solution {
public:int lengthOfLIS(vector<int>& nums) {//每个都得初始是1,不能是0,不能只初始最后一个位置是1//可能有的数往后都是比它小的,那它也不能是0,而是1int n=nums.size();vector<int> dp(n,1);int ret=0;for(int i=n-1;i>=0;--i){for(int j=i+1;j<n;++j){if(nums[j]>nums[i]){dp[i]=max(dp[i],dp[j]+1);}}//得到i位置往后最大递增子串,判断ret=max(ret,dp[i]);}return ret;}
};四、猜数字大小II
375. 猜数字大小 II - 力扣(LeetCode)

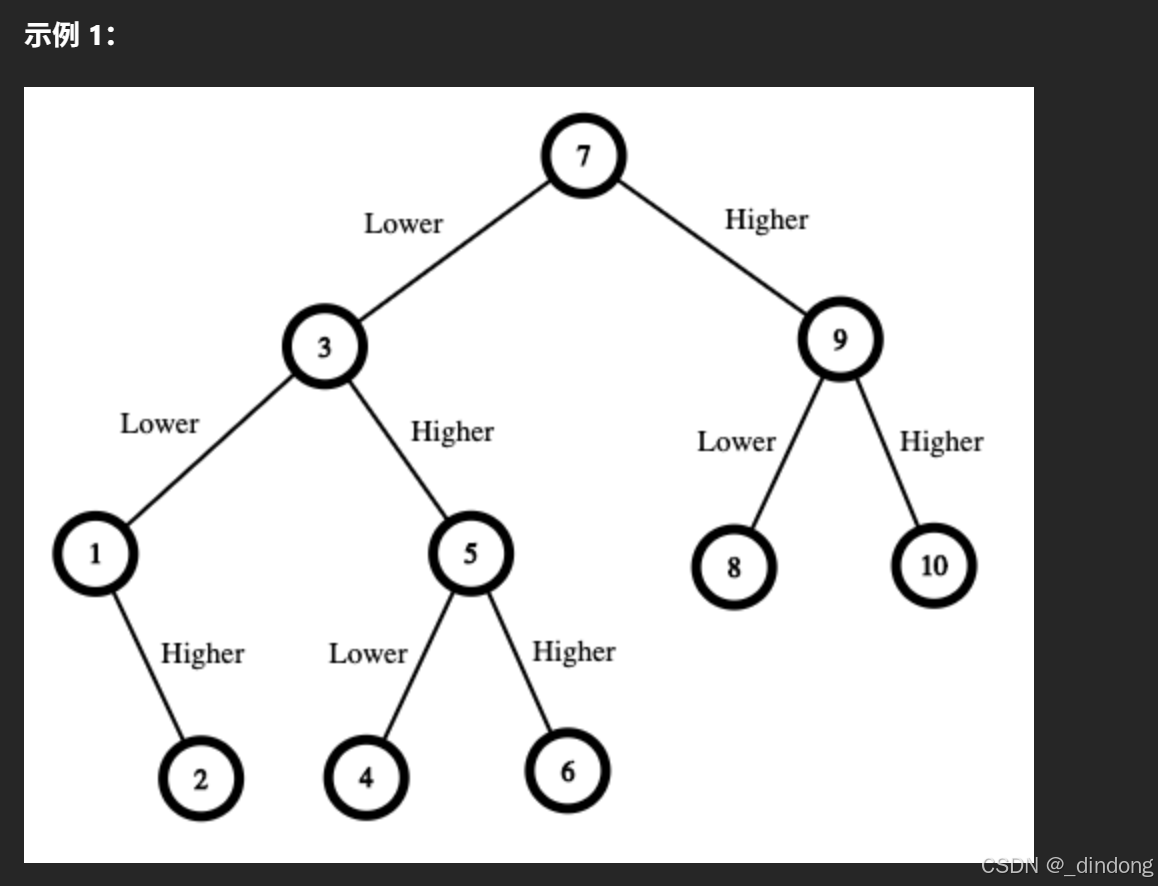


没记错的话,贪心章节也会提及这题
有了第一道猜数字,可能会考虑二分,如果答案是10,那么这个策略来猜,
花销是很大的。所以二分并不是最好的策略,因为我们要的不是最小次数,而是最小保证赢的金额,也就是往大值里找最小值。
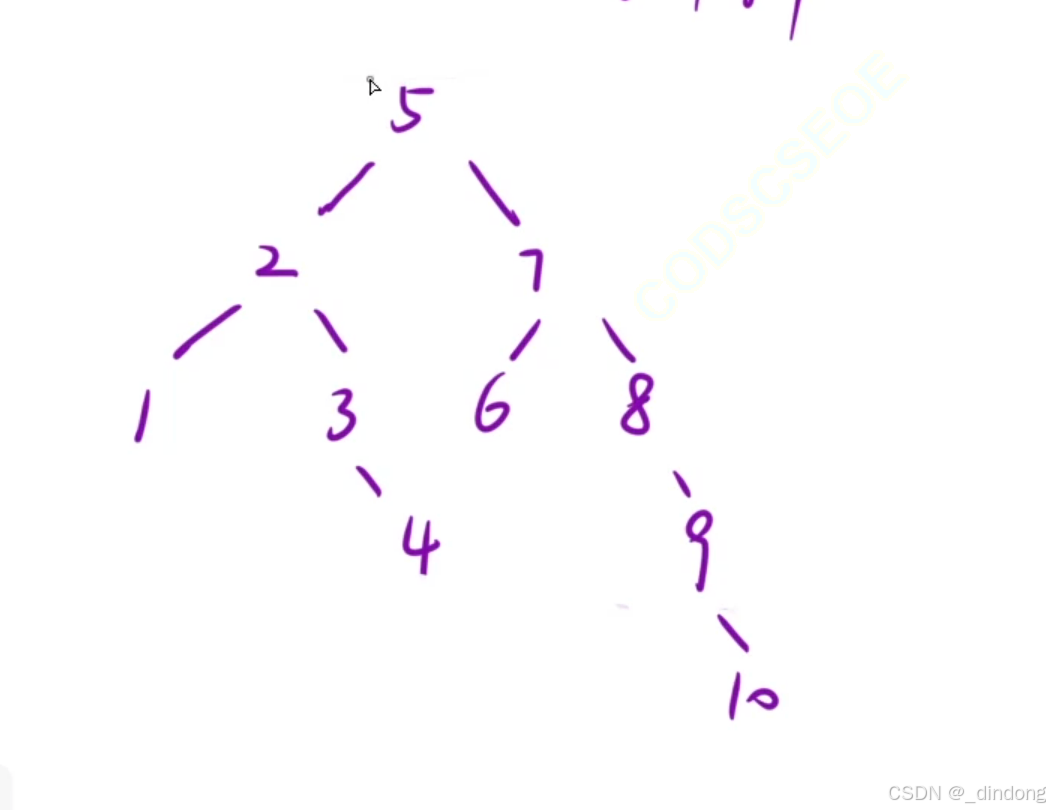
问题的核心在于,答案的不确定性,所以为了确保你的钱够付得起所有结果,你得准备的钱一定得是你这个分支,往更大的地方猜测去准备你的本金,这样就算数是更小部分,我们准备的钱也足够我们获胜。
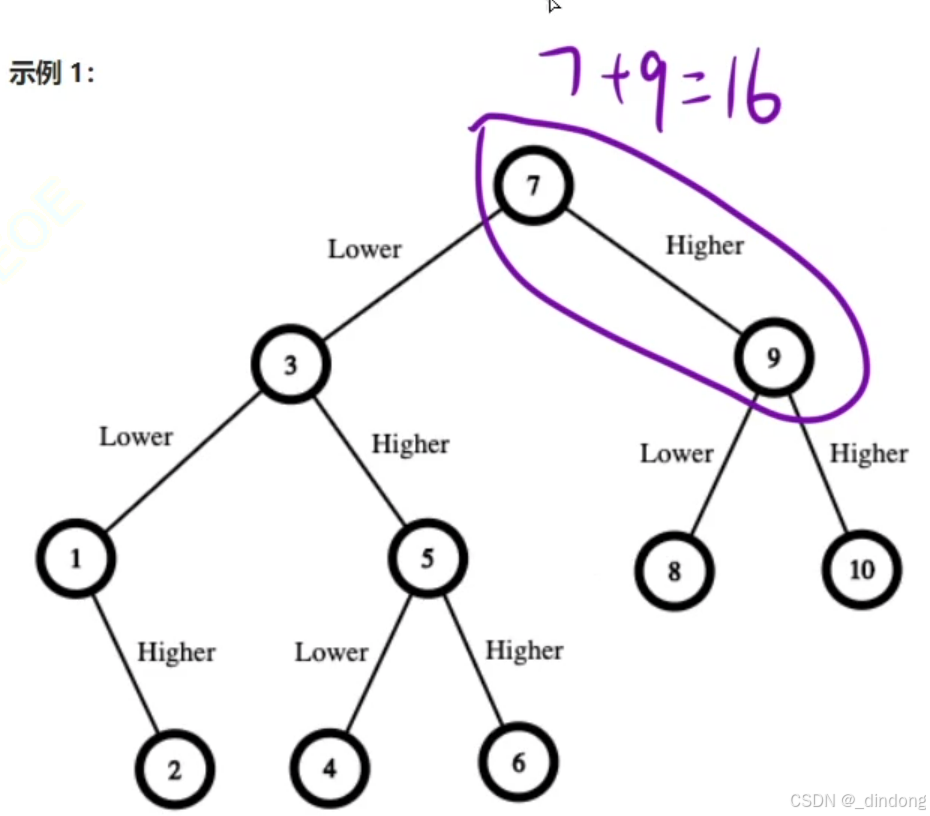
博弈,枚举从1~n当作头,然后往下递归处理子问题
递归每层处理,都往大的地方考虑,求下层所有递归结果的,里的最小值
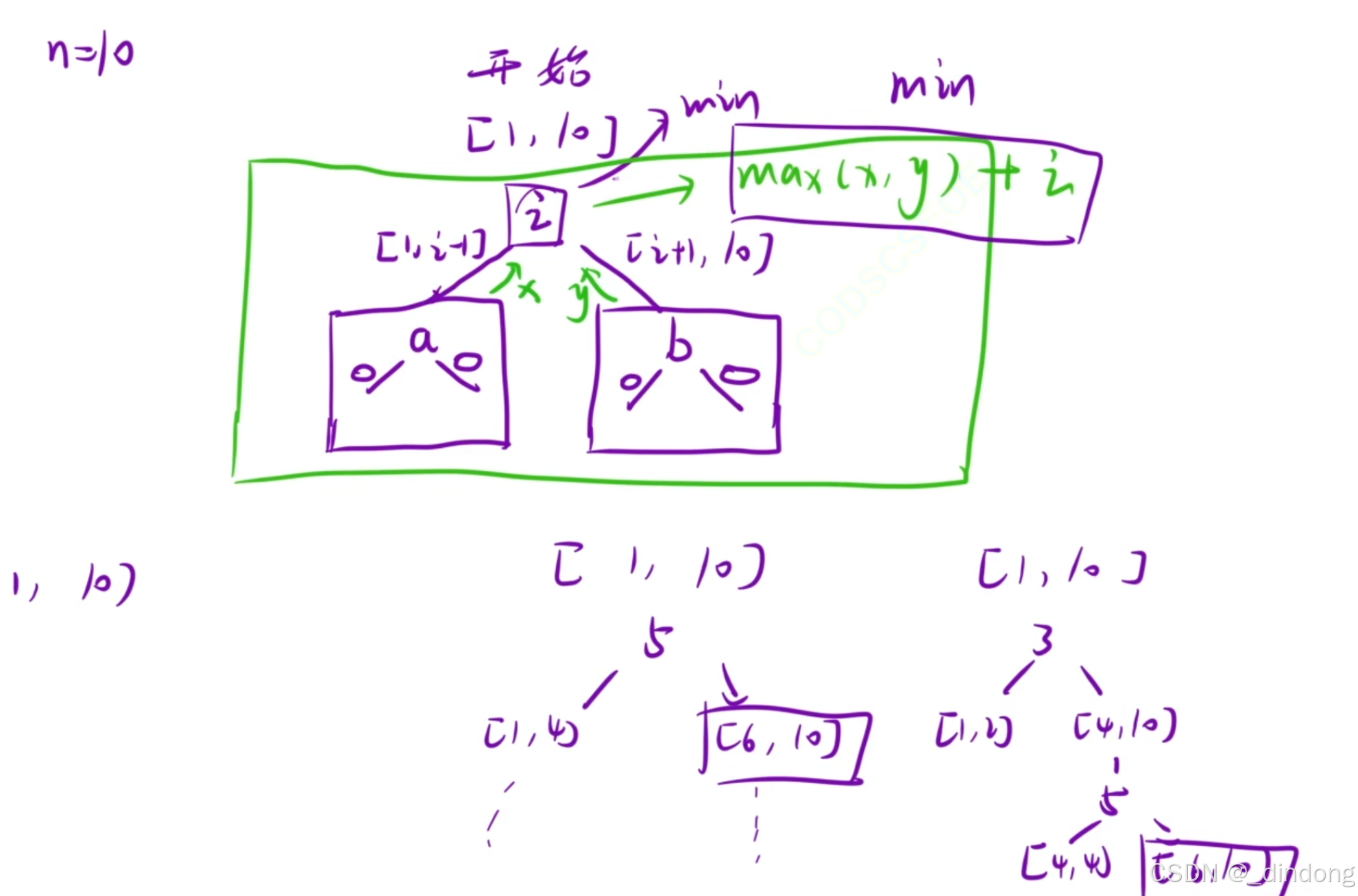
记忆化搜索+dfs实现
class Solution {int memo[201][201];
public:int getMoneyAmount(int n) {return dfs(1,n);}int dfs(int left,int right){if(left>=right)return 0;if(memo[left][right]!=0)return memo[left][right];int ret=INT_MAX;for(int head=left;head<=right;++head){//x:左子树处理结果 y:右子树处理结果int x=dfs(left,head-1);int y=dfs(head+1,right);//max(x,y)保证赢需要往大了考虑ret=min(ret,head+max(x,y));}//更新该区间的保证赢的最少花费memo[left][right]=ret;return ret;}
};五、矩阵中的最长递增路径
329. 矩阵中的最长递增路径 - 力扣(LeetCode)


有了前面的铺垫,这道困难题就易如反掌了
class Solution {int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1},m,n;int memo[201][201];
public:int longestIncreasingPath(vector<vector<int>>& matrix) {m=matrix.size(),n=matrix[0].size();int ret=0;for(int i=0;i<m;++i){for(int j=0;j<n;++j){ret=max(ret,dfs(matrix,i,j));}}return ret;}int dfs(vector<vector<int>>& matrix,int i,int j){if(memo[i][j]!=0)return memo[i][j];int path=1;for(int k=0;k<4;++k){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&matrix[x][y]>matrix[i][j]){path=max(path,dfs(matrix,x,y)+1);}}memo[i][j]=path;return path;}
};此专栏完结撒花*★,°*:.☆( ̄▽ ̄)/$:*.°★* 。
感谢收看。
