跟着小码学算法Day20：构造二叉树

目录

一、通用前提

二、构造方法

1、前序 + 中序 构造二叉树

核心思路

解题步骤

2、中序 + 后序 构造二叉树

核心思路

解题步骤

三、通用模板

四、典型例题

一、通用前提

要唯一构造一棵二叉树，通常需要两种遍历方式的组合，因为单一遍历无法确定树的结构。

关键：找到根节点，并划分左右子树。

遍历方式	遍历顺序	特点
前序 (Preorder)	根 → 左 → 右	第一个元素是根
中序 (Inorder)	左 → 根 → 右	可以通过根划分左右子树
后序 (Postorder)	左 → 右 → 根	最后一个元素是根

二、构造方法

1、前序 + 中序 构造二叉树

核心思路

以前序遍历确定根节点，以中序遍历划分左右子树。

• 前序遍历的第一个元素是当前树的根节点。
• 在中序遍历中找到这个根的位置，那么：
  • 根左边的所有元素 → 属于左子树
  • 根右边的所有元素 → 属于右子树
• 左子树的节点数量决定了前序遍历中左子树的范围。

解题步骤

1. 取 preorder[0] 作为当前根节点。
2. 在 inorder 中查找该根的位置 index。
3. 计算左子树节点数：leftSize = index - inLeft。
4. 划分左右子树范围：
   • 左子树：
     • 中序：[inLeft, index)
     • 前序：[preLeft + 1, preLeft + 1 + leftSize)
   • 右子树：
     • 中序：[index + 1, inRight)
     • 前序：[preLeft + 1 + leftSize, preRight)
5. 递归构建左右子树，并挂到根节点上。
6. 返回根节点。

---

2、中序 + 后序 构造二叉树

核心思路

以后序遍历确定根节点，以中序遍历划分左右子树。

• 后序遍历的最后一个元素是当前树的根节点。
• 在中序遍历中找到这个根的位置，那么：
  • 根左边 → 左子树
  • 根右边 → 右子树
• 左子树的节点数量决定了后序遍历中左子树的范围。

解题步骤

1. 取 postorder[postRight - 1] 作为当前根节点。
2. 在 inorder 中查找该根的位置 index。
3. 计算左子树节点数：leftSize = index - inLeft。
4. 划分左右子树范围：
   • 左子树：
     • 中序：[inLeft, index)
     • 后序：[postLeft, postLeft + leftSize)
   • 右子树：
     • 中序：[index + 1, inRight)
     • 后序：[postLeft + leftSize, postRight - 1)（去掉最后一个根）
5. 递归构建左右子树，并挂到根节点上。
6. 返回根节点。

---

三、通用模板

Map<Integer, Integer> map = new HashMap<>();public TreeNode buildTree(int[] inorder, int[] xxxorder) {// xxxorder 是 preorder 或 postorderfor (int i = 0; i < inorder.length; i++) {map.put(inorder[i], i);}return build(inorder, 0, inorder.length,xxxorder, 0, xxxorder.length);
}private TreeNode build(int[] inorder, int inLeft, int inRight,int[] xxxorder, int xLeft, int xRight) {if (inLeft >= inRight || xLeft >= xRight) return null;// 根据遍历方式取根int rootVal = (xxxorder == preorder) ? xxxorder[xLeft] :           // 前序：第一个xxxorder[xRight - 1];       // 后序：最后一个TreeNode root = new TreeNode(rootVal);int index = map.get(rootVal); // 中序中根的位置int leftSize = index - inLeft;// 前序 + 中序if (使用前序) {root.left  = build(inorder, inLeft, index,xxxorder, xLeft + 1, xLeft + 1 + leftSize);root.right = build(inorder, index + 1, inRight,xxxorder, xLeft + 1 + leftSize, xRight);}// 中序 + 后序else {root.left  = build(inorder, inLeft, index,xxxorder, xLeft, xLeft + leftSize);root.right = build(inorder, index + 1, inRight,xxxorder, xLeft + leftSize, xRight - 1);}return root;
}

四、典型例题

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

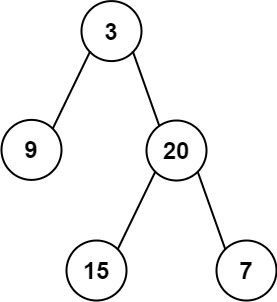
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

解法

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {Map<Integer, Integer> map;public TreeNode buildTree(int[] preorder, int[] inorder) {map = new HashMap<>();// 将中序遍历的值和索引存入 mapfor (int i = 0; i < inorder.length; i++) {map.put(inorder[i], i);}return findNode(preorder, 0, preorder.length,inorder, 0, inorder.length);}public TreeNode findNode(int[] preorder, int preLeft, int preRight,int[] inorder, int inLeft, int inRight) {// 终止条件if (preLeft >= preRight || inLeft >= inRight) {return null;}// 前序遍历的第一个元素是根节点int rootVal = preorder[preLeft];TreeNode node = new TreeNode(rootVal);// 在中序遍历中找到根的位置int rootIndexInInorder = map.get(rootVal);// 计算左子树的节点数量int leftTreeSize = rootIndexInInorder - inLeft;// 递归构建左子树// preorder: [preLeft+1, preLeft+1+leftTreeSize)// inorder:  [inLeft, rootIndexInInorder)node.left = findNode(preorder, preLeft + 1, preLeft + 1 + leftTreeSize,inorder, inLeft, rootIndexInInorder);// 递归构建右子树// preorder: [preLeft+1+leftTreeSize, preRight)// inorder:  [rootIndexInInorder+1, inRight)node.right = findNode(preorder, preLeft + 1 + leftTreeSize, preRight,inorder, rootIndexInInorder + 1, inRight);return node;}
}

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

解法

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {Map<Integer, Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map = new HashMap<>();// 将中序遍历的值和索引存入 map，便于快速查找根的位置for (int i = 0; i < inorder.length; i++) {map.put(inorder[i], i);}return findNode(inorder, 0, inorder.length, postorder, 0, postorder.length);}public TreeNode findNode(int[] inorder, int inLeft, int inRight,int[] postorder, int postLeft, int postRight) {// 终止条件if (inLeft >= inRight || postLeft >= postRight) {return null;}// 后序遍历的最后一个元素是当前子树的根节点int rootVal = postorder[postRight - 1];TreeNode node = new TreeNode(rootVal);// 在中序遍历中找到根节点的位置int rootIndexInInorder = map.get(rootVal);// 计算左子树的节点数量int leftTreeSize = rootIndexInInorder - inLeft;// 递归构建左子树// 中序：[inLeft, rootIndexInInorder)// 后序：[postLeft, postLeft + leftTreeSize)node.left = findNode(inorder, inLeft, rootIndexInInorder,postorder, postLeft, postLeft + leftTreeSize+1);// 递归构建右子树// 中序：[rootIndexInInorder + 1, inRight)// 后序：[postLeft + leftTreeSize, postRight - 1)node.right = findNode(inorder, rootIndexInInorder + 1, inRight,postorder, postLeft + leftTreeSize, postRight - 1);return node;}
}