电力电子技术 第十一章——谐波分析与功率因数校正
参考教程:https://www.bilibili.com/video/BV1pS4y1g7D9?spm_id_from=333.788.videopod.episodes&vd_source=8f8a7bd7765d52551c498d7eaed8acd5
一、交流电和谐波的概念
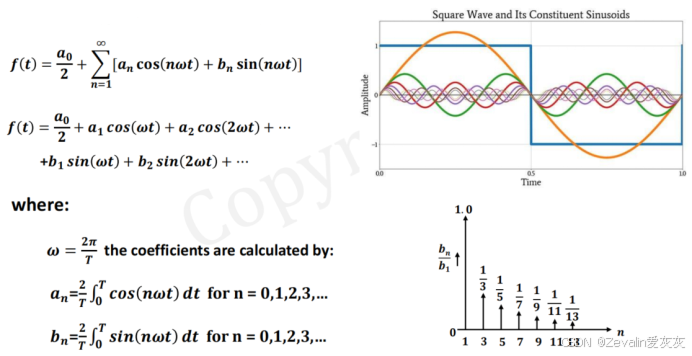
1、交流信号的傅里叶级数展开
对于一个周期信号可以用傅里叶级数将其展开,得到一个基波(直流量)和若干个谐波(交流量),如下所示
2、有效值的概念
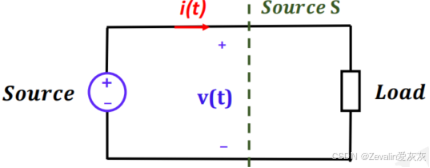
下图所示是一个简单的电路,输入侧的能量将经过S平面流向输出侧
用傅里叶级数将电流和电压关于时间的函数展开,可得
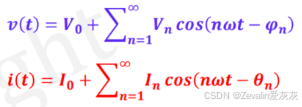
由于它们都是周期函数且周期相同,假定T为最小正周期,那么不难得出流过S平面的平均功率为
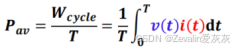
将傅里叶级数展开的结果代入其中,可得
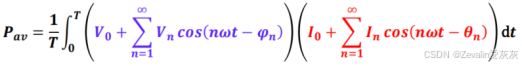
根据谐波的正交性,有
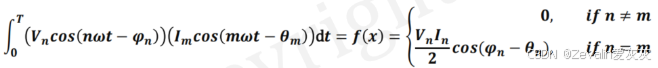
因此平均功率可以表示为
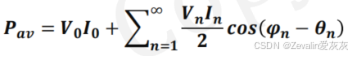
这也间接说明了,只有当电流和电压的傅里叶级数中包含相同频率的项时,净能量才会被传输到负载,否则,即使某一时刻负载的瞬时功率不为零,从平均的结果看,负载也是收不到能量的
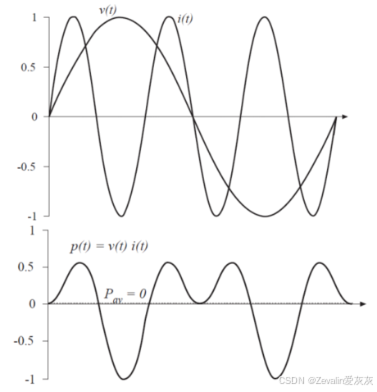
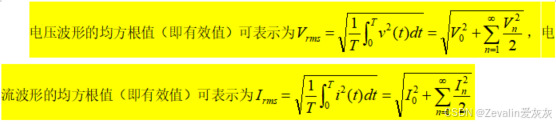
有效值与平均值不同,谐波会增加有效值,却不一定增加平均值,这部分差值就是电路的损耗
3、功率因数
为了从电源端高效传输能量到负载,通常希望最大化平均功率,同时最小化有效值电流和有效值电压,从而最小化损耗,对此定义功率因数衡量能量传输效率,有

当负载为线性电阻且输入电压为非正弦量时,电流谐波与电压谐波同相位且成比例,所有谐波的能量都会传输至负载,此时功率因数为1
当负载为非线性电阻且输入电压为正弦量时,电流谐波(与输入电压不同频的谐波分量)不会增加平均功率,但由于增加了有效值电流,因此将降低功率因数
二、可控整流器的谐波分析
1、单相桥式全控整流器的谐波分析
下图所示的是负载为电阻串联电感的单相桥式全控整流器原理图及其输入输出波形,假设电感感值非常大,输出电流可视为是恒定的。
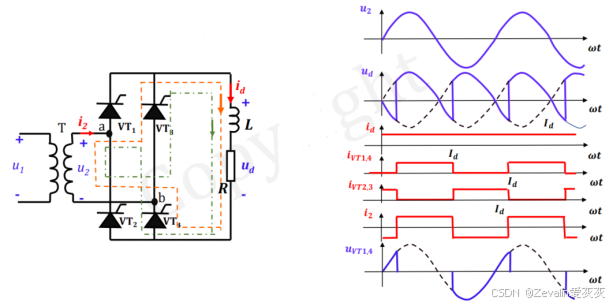
对输入电流用傅里叶级数展开,有
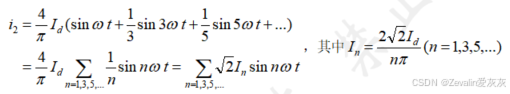
不难发现输入电流的一次谐波分量与输入电压同频
畸变因子等于输入电流一次谐波分量除以输入电流有效值,即
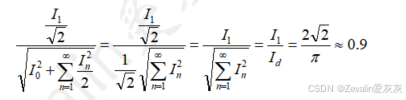
位移因子等于
最终可得功率因数约等于
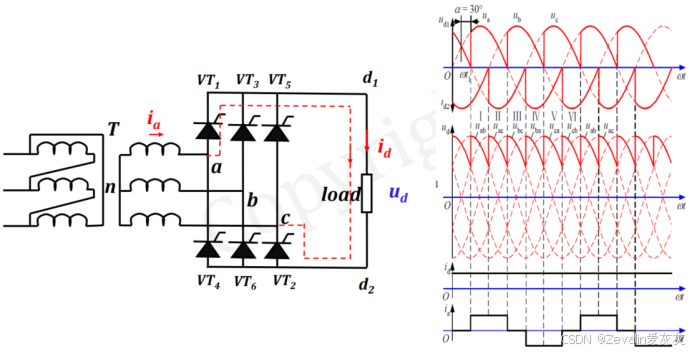
2、三相全桥控制整流器的谐波分析
下图所示的是负载为电阻串联电感的三相全桥控制整流器原理图及其输入输出波形,假设电感感值非常大,输出电流可视为是恒定的
对输入电流用傅里叶级数展开,有
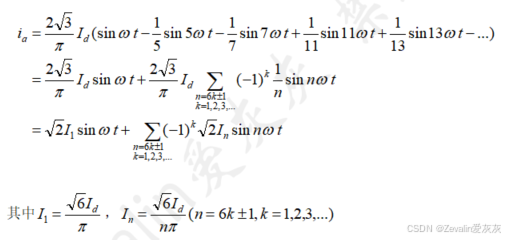
不难发现输入电流的一次谐波分量与输入电压同频
畸变因子等于输入电流一次谐波分量除以输入电流有效值,即
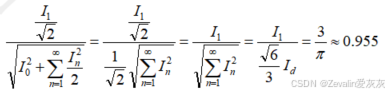
位移因子等于
最终可得功率因数约等于
三、不可控整流器的谐波分析
下图所示的是一个单相不可控全波整流器,负载为标配的L-C-R
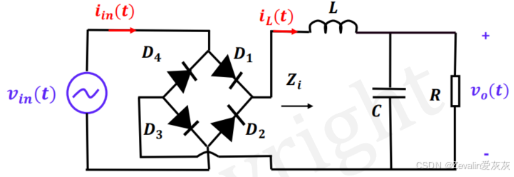
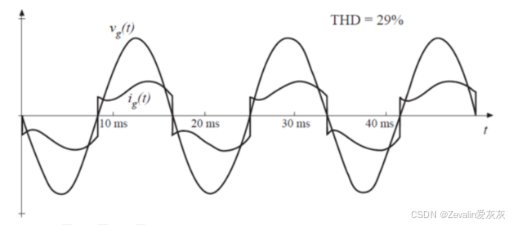
当输出侧电感感值较大时,电感电流趋于恒定,此时输入侧电流的波形趋近于理想的方波,对其做傅里叶级数展开,可以得到与输入电压同频的一次谐波,这时畸变因子是比较大的
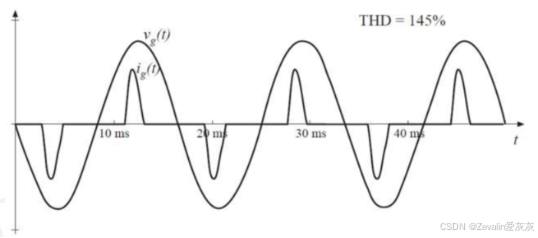
然而,实际中电感无法做到感值无穷大,如果电感感值过小,那么不难得出二极管的导通时间也会很小(可以直接考虑极端情况,负载为R-C,感值为0),这时再对其做傅里叶级数展开,畸变因子显然会比前者小很多
四、功率因数校正
1、使用无源器件进行功率因数校正
根据前面单相不可控全波整流器的例子,不难得出,如果要改善整流器的功率因数,可以采用增加滤波器件的方法,不过它对功率因数的改善是有限的
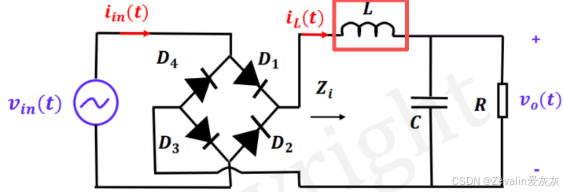
2、使用有源器件进行功率因数校正
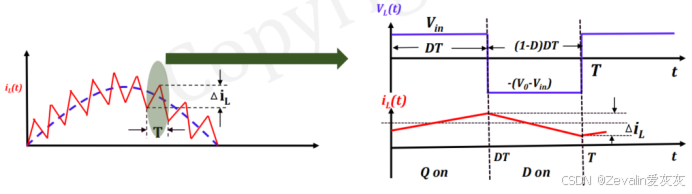
继续以单相不可控全波整流器为例,如果不引入有源器件,畸变因子的改善是有限的,对此可以考虑使用有源器件控制输出侧的状态,使得输出电流的整体变化趋势跟随输入电压,如下图所示
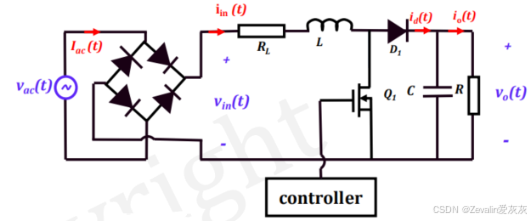
在晶体管的一个开关周期内(开关周期比输入电压的周期小不少),电感电流的变化并不是平滑的,当晶体管开通时,二极管D1被动关断,此时电压将全部加在电感上,而当晶体管关断时,二极管D1被动导通,由于输出侧是一个Boost电路,因此
一定是大于
的,根据基尔霍夫电压定律可得电感电压为
,电感电压“正负来回跳变”,从而导致电感电流“升降来回振荡”
由于晶体管的开关周期短,电感电流的振荡幅度小,并且因为不同开关周期电感电压的上下界是不同的(或者说不同),电感不满足伏秒平衡,这就使得电感电流的整体趋势跟随电压