深入理解跳表:数据结构解析与应用
011. 跳表概述和工作原理
> 1.1. 跳表简介与特点
跳表,这一数据结构虽然在大学本科教材中鲜有提及,但在工业界有着广泛的应用。其插入、删除、查找元素的时间复杂度与红黑树相当,均为O(logn)。更值得一提的是,跳表还具备红黑树所不具备的独特特性。接下来,我们将深入探讨跳表的工作原理及其在工业界的应用场景。
在了解跳表之前,我们首先从单链表谈起。单链表,一种基础的数据结构,通过每个元素存储的下一个元素引用,实现元素的顺序访问。这种特性使得我们可以通过链表中的第一个元素,逐步找到后续的每一个元素。而跳表,则是在单链表的基础上,通过引入多级索引,实现了更高效的查找、插入和删除操作。
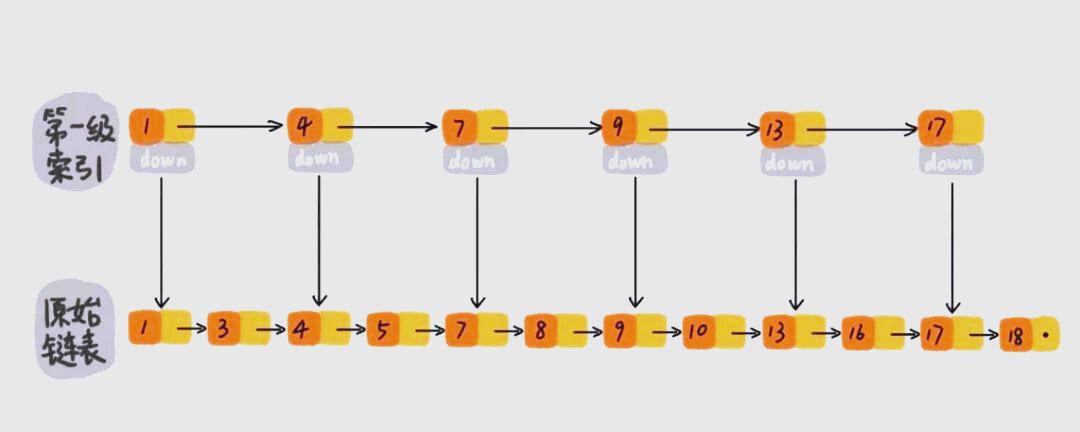
> 1.2. 跳表索引实现
现在,我们面临一个场景,需要迅速在链表中定位到元素10,但若仅从头开始逐个遍历,效率将非常低下,平均时间复杂度为O(n)。这样的查找路径:1、3、4、5、7、8、9、10,显然不是我们期望的高效方法。那么,有没有策略能提升链表的查找速度呢?答案是肯定的。我们可以考虑在链表中每隔一定数量的元素抽取出来,并为这些元素建立索引。例如,我们可以每隔一个元素抽取一个,这样原始链表就被划分为多个子链表。
通过这种方式,我们可以迅速定位到任何一个子链表,进而找到目标元素。那么,现在该如何查找元素10呢?
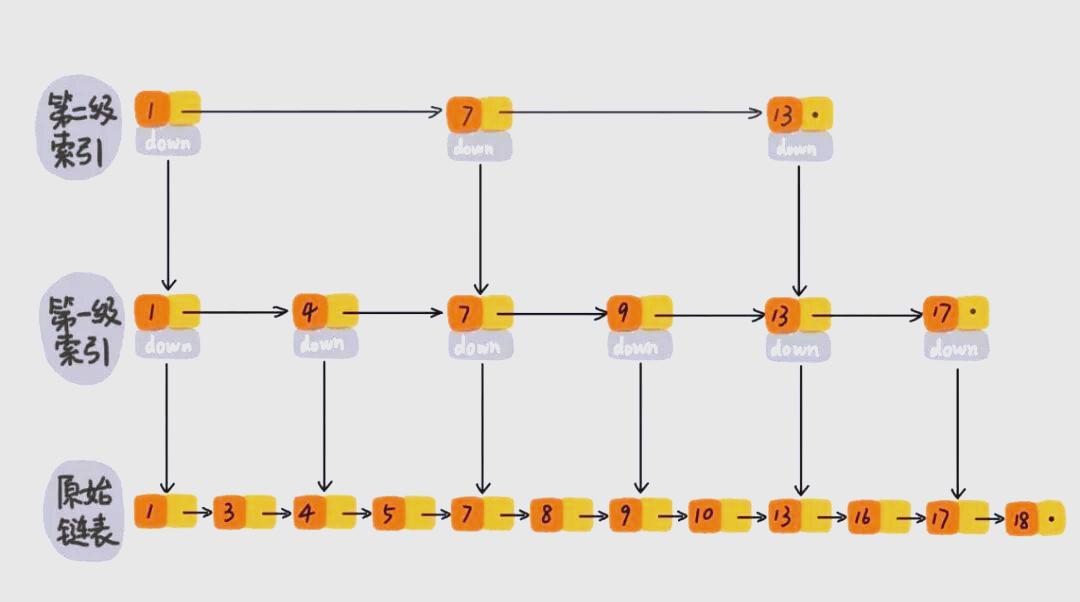
022. 查找、插入与删除操作
> 2.1. 高效查找路径
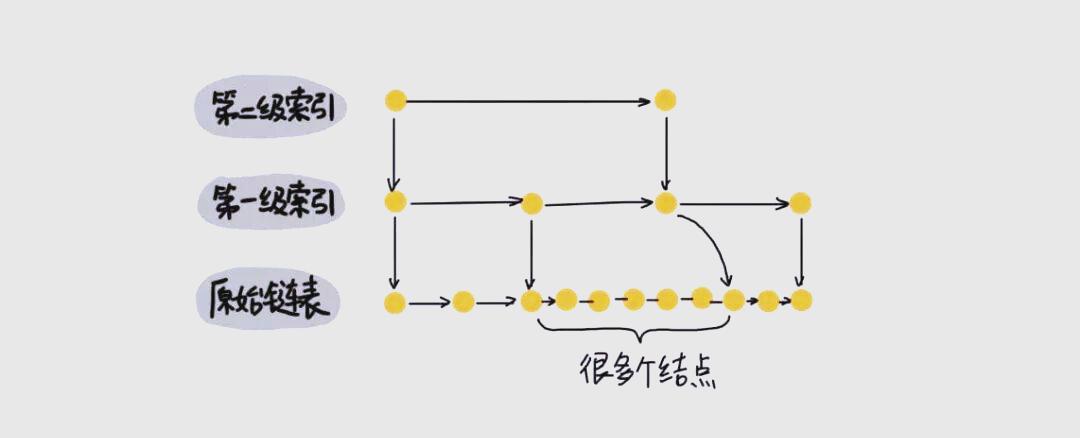
首先,我们利用索引快速定位到1、4、7、9这些关键节点。在遍历到一级索引的9时,发现其后续节点是13,这比目标元素10大,因此我们不必再继续向后查找。相反,我们通过9节点找到原始链表中的9,然后仅需向后遍历一步,即可找到我们需要的10。这样的查找路径:1、4、7、9、10,显然减少了需要遍历的元素数量,从而大大提高了查找效率。当进一步引入二级索引时,查找路径缩短为:1、7、9、10。显然,这样查找10的效率会更高。
这一显著的效率提升在大数据量情况下尤为明显。例如,对于包含1万个元素的有序单链表,通过建立多级索引,可以将查找时间复杂度大幅降低。跳表通过多级索引,尤其在大数据量情况下,将查找元素的时间复杂度大幅降低。
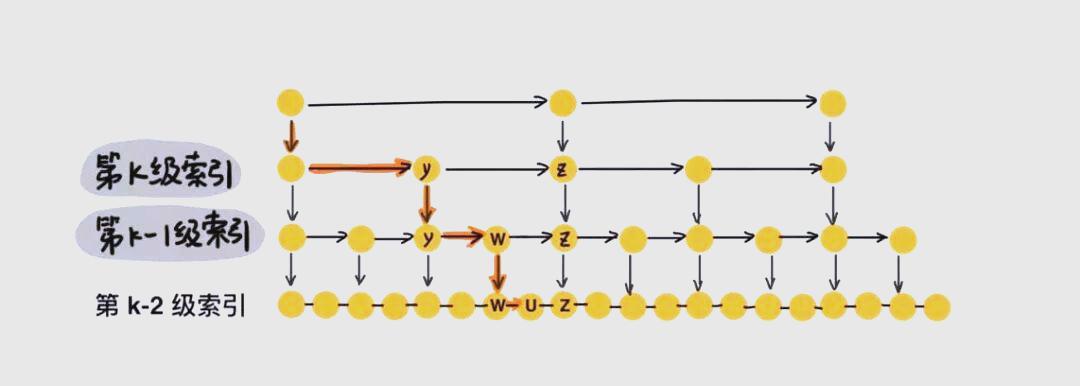
> 2.2. 插入操作
接下来,插入操作如何遵循随机索引策略以及保持索引同步的方法呢?插入新数据时,我们会仿照查找元素的路径来定位插入位置。例如,要插入数据6,整个过程类似于查找6的路径:1、1、1、4、4、5。当查找到最底层的原始链表元素5时,发现5小于6但后继节点7大于6,因此我们应将6插入到5与7之间。整个插入操作的时间复杂度与查找元素相同,为O(logn)。插入操作通过随机算法来维护多级索引的均衡,避免索引重建,以保证操作的高效性。
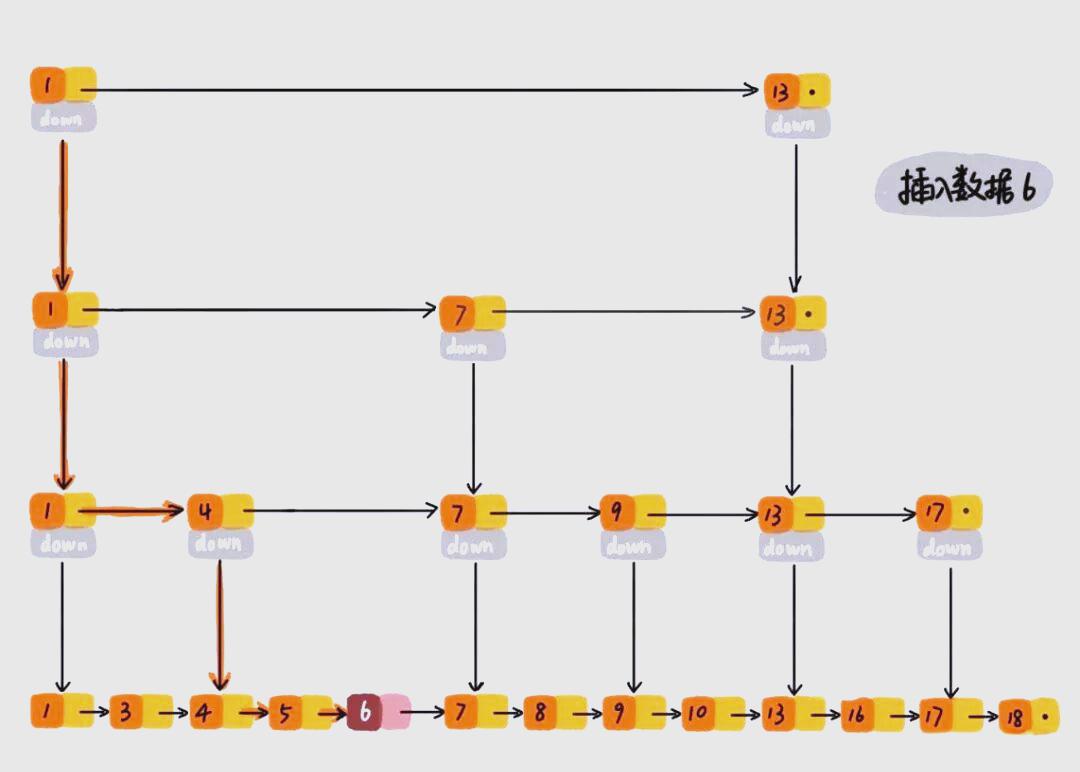
> 2.3. 删除操作
最后,我们探讨一下删除操作。在跳表中删除数据时,不仅需要删除原始链表中的对应节点,还需要同时删除索引中的相应节点。删除操作不仅需要删除原链表节点,还需删除各级索引中的关联节点,时间复杂度仍然为O(logn)。
033. 空间复杂度与实际应用
> 3.1. 索引空间影响
接下来,我们来看跳表的空间复杂度。由于跳表通过建立索引来提高查找效率,这体现了“空间换时间”的思想,因此在空间上有所牺牲。虽然增加了索引导致空间复杂度变为O(n),但优化的抽选策略能有效减少额外空间损耗。
> 3.2. 跳表与数据库应用
值得注意的是,跳表因其高效的查找与插入特性,在数据库内存存储和查找优化中得到了广泛应用。HBase MemStore的数据结构中采用了跳表来存储数据。不仅如此,跳表在数据库内存存储系统中得到了广泛应用,如HBase、LevelDB等
