opencv学习笔记8:haar特征、决策树、adaboost初步认识
目录
一、Haar 特征
1.概述
2.Haar 特征的本质
3.常见的 Haar 特征卷积核
4.积分图
5.haar特征计算示例
二.决策树和随机森林简介
1.决策树
(1)决策树的组成
2.随机森林
三.adaboost算法简介
1.感性认识
1. 先理解两个关键角色
2. 核心逻辑:让弱分类器 “取长补短”
第一步:找第一个 “菜鸟”(弱分类器 1)
第二步:找第二个 “菜鸟”(弱分类器 2)
第三步:重复找 “菜鸟”
第四步:凑成 “专家团”(强分类器)
总结:AdaBoost 就是
2.正式介绍
一、Haar 特征
1.概述
Haar 特征提取是计算机视觉中用于目标检测的经典特征提取方法,尤其在 Viola-Jones 目标检测框架中被广泛应用(如人脸检测)。其核心思想是通过计算图像中不同区域的像素值差异,捕捉目标的边缘、纹理、明暗变化等局部特征。以下是 Haar 特征提取的详细解析:
2.Haar 特征的本质
Haar 特征基于Haar 小波的思想,通过设计简单的矩形模板(特征模板),计算模板内不同区域的像素和之差,来描述图像的局部灰度变化。
- 直观理解:模板中白色区域的像素和减去黑色区域的像素和,结果即为该位置的 Haar 特征值。
- 核心作用:快速捕捉目标的关键结构(如人脸的眼睛比脸颊暗、鼻梁比两侧亮等)。
3.常见的 Haar 特征卷积核
Haar 特征卷积核通常由相邻的黑白矩形组成,常见类型包括:
- 边缘特征:如水平边缘(黑白上下矩形)、垂直边缘(黑白左右矩形)。
- 例:可用于检测人脸的眉毛与额头的明暗边界。
- 线特征(内部特征):如水平三线(白 - 黑 - 白)、垂直三线(白 - 黑 - 白)。
- 例:可用于检测人脸的鼻梁(中间亮、两侧暗)。
- 中心环绕特征:如中心白、周围黑的矩形,或反之。
- 例:可用于检测人脸的眼睛(中心暗、周围亮)。
每个卷积核可以通过缩放(改变大小) 和平移(改变位置) 覆盖图像的不同区域,生成大量特征。

如上图中,一种卷积核表示一种Haar特征,大小不同也能得到不同的Haar特征。其应用思路如下,考虑人脸检测,Haar特征能够识别出人脸的关键部位。如下图,检测眉毛位置使用图中所示意的Haar特征,因眉毛处的像素比额头处要暗,也就是灰度值小,拿矩形白色部分的像素和减去黑色矩形的像素和,能得到比其他部位更大的灰度插值。同样,对鼻子处,左右部分也存在灰度差值。

计算过程就是黑色矩形区域内像素值之和减去白色矩形区域内像素值之和,计算过程其实很简单。但是,直接计算的话,针对每一个矩形区域,我们都需要做一次循环,计算区域内像素之和,对每个位置进行滑窗遍历进行Haar特征提取会使得计算量爆炸,因此,一般Haar特征会配合积分图技术一起来使用。
4.积分图
积分图计算如下图所示,经过计算后,积分图中每个点对应值Inter(x,y)为对应蓝色矩形区域像素值之和。
当需要提取Haar特征时,我们需要计算矩形块中像素值之和时,我们只需要将其四个顶点对应于积分图中的值拿出来,做一个求和操作即可,计算过程如下图所示。
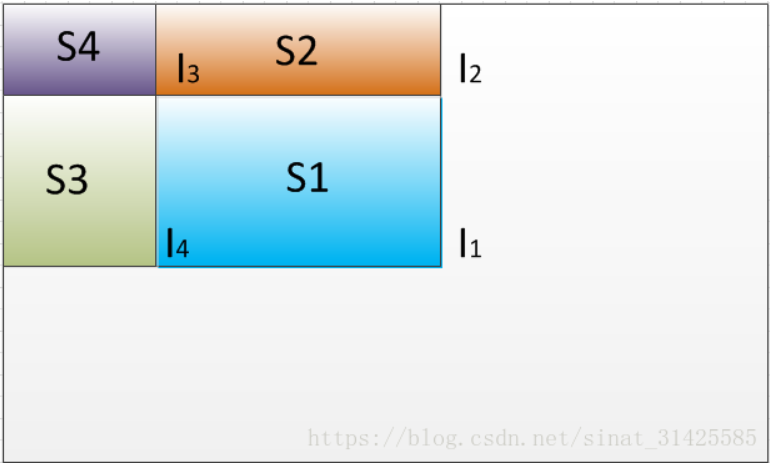
上图中S1区域为要提取特征区域,I1,I2,I3,I4分别对应四个顶点位置对应于积分图中的值,由积分图计算过程不难发现:
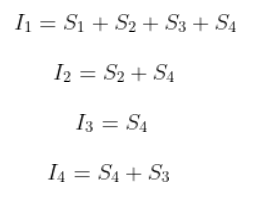
因此,,一个矩形区域内像素累加求和计算转变成了几个值的加减运算,大大的提升了算法执行效率。
举例:右侧就是积分图,例如417就是左上方四个方格相加
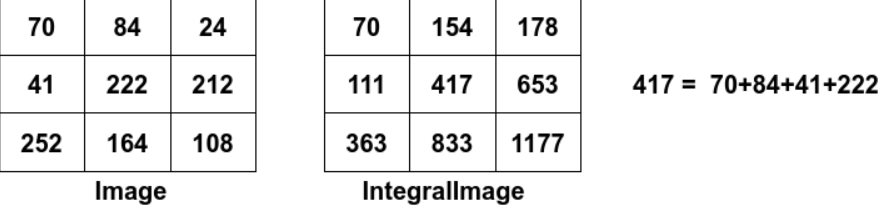
5.haar特征计算示例
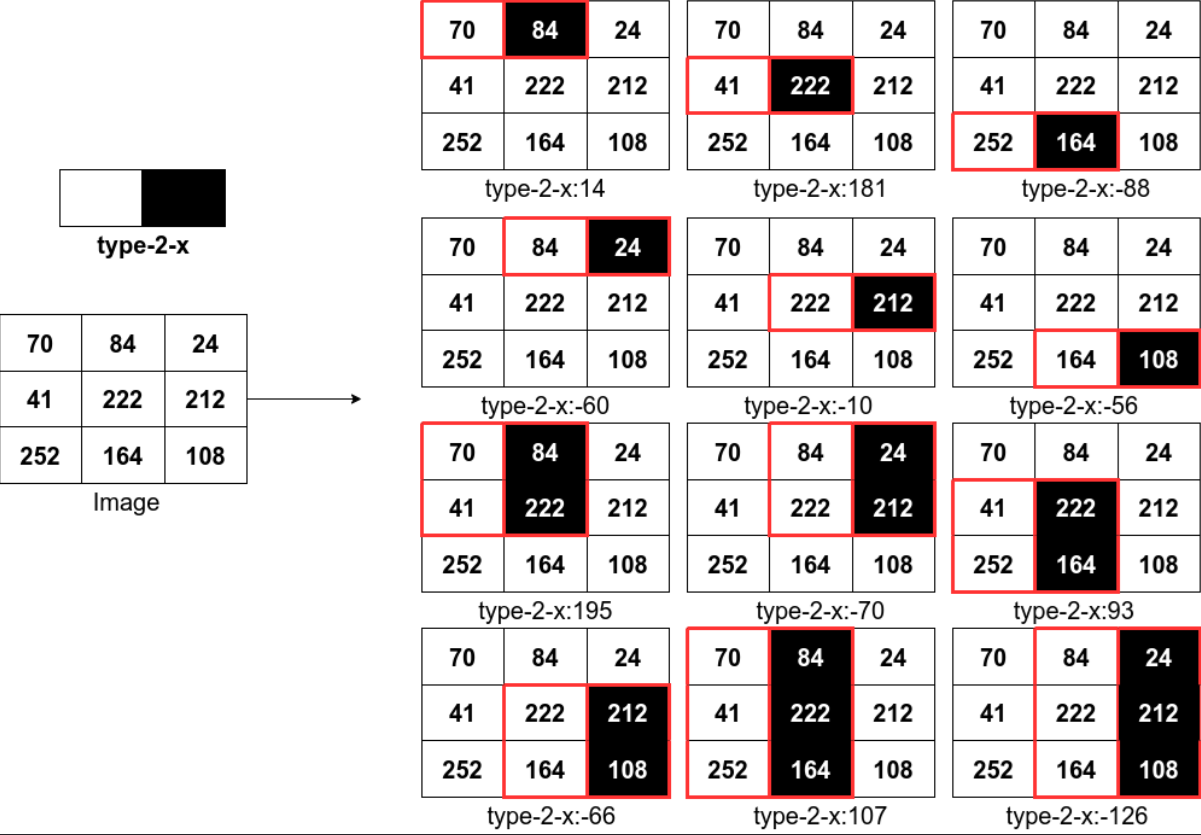
下图表示的是对一个3x3大小的图像求type-2-x模式的Haar特征的过程,即黑色区域像素和减去白色区域像素和。一个宽高3x3的图像,经过rescale的type-2-x的Haar变换可以得到12个特征值。当图像尺度变大时能够得到更多的Haar特征。对一个宽高8x8的图像,type-2-x的Haar变换可以得到576个特征值;而对一个宽高56x56的图像,type-2-x的Haar变换可以得到1251264个特征值。
二.决策树和随机森林简介
1.决策树
决策树(Decision Tree)是一种分类和回归方法,是基于各种情况发生的所需条件构成决策树,以实现期望最大化的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。它的运行机制非常通俗易懂,因此被誉为机器学习中,最“友好”的算法。下面通过一个简单的例子来阐述它的执行流程。假设根据大量数据(含 3 个指标:天气、温度、风速)构建了一棵“可预测学校会不会举办运动会”的决策树(如下图所示)。
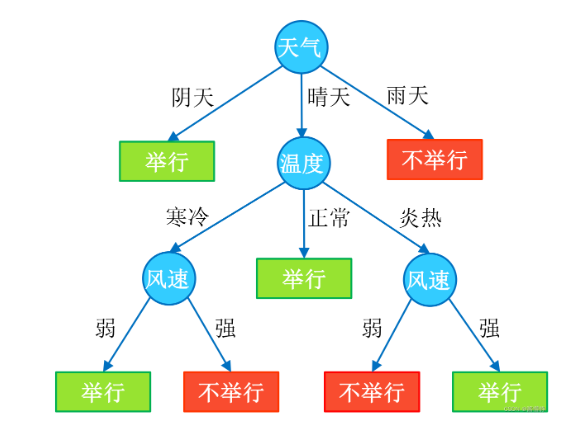
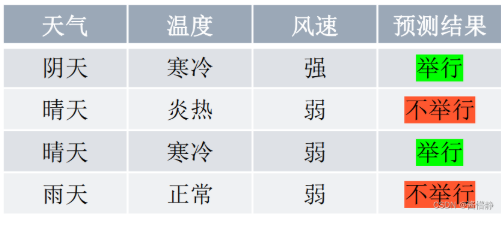
在对任意数据进行预测时,都需要从决策树的根结点开始,一步步走到叶子结点(执行决策的过程)。如,对下表中的第一条数据( [ 阴天,寒冷,强 ] ):首先从根结点出发,判断 “天气” 取值,而该数据的 “天气” 属性取值为 “阴天”,从决策树可知,此时可直接输出决策结果为 “举行”。这时,无论其他属性取值为什么,都不需要再执行任何决策(类似于 “短路” 现象)。
(1)决策树的组成
决策树由结点和有向边组成。结点有两种类型:内部结点(圆)和叶结点(矩形)。其中,内部结点表示一个特征(属性);叶结点表示一个类别。而有向边则对应其所属内部结点的可选项(属性的取值范围)。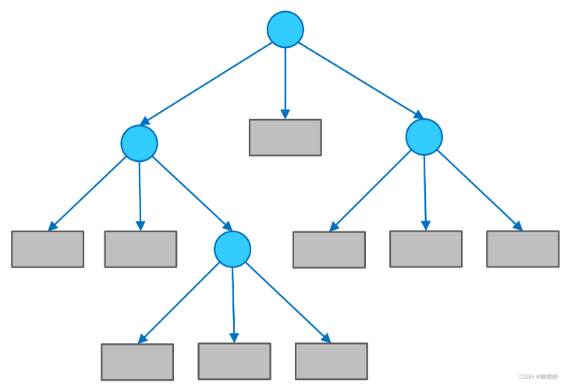
在用决策树进行分类时,首先从根结点出发,对实例在该结点的对应属性进行测试,接着会根据测试结果,将实例分配到其子结点;然后,在子结点继续执行这一流程,如此递归地对实例进行测试并分配,直至到达叶结点;最终,该实例将被分类到叶结点所指示的结果中。
在决策树中,若把每个内部结点视为一个条件,每对结点之间的有向边视为一个选项,则从根结点到叶结点的每一条路径都可以看做是一个规则,而叶结点则对应着在指定规则下的结论。这样的规则具有互斥性和完备性,从根结点到叶结点的每一条路径代表了一类实例,并且这个实例只能在这条路径上。从这个角度来看,决策树相当于是一个 if-then 的规则集合,因此它具
有非常好的可解释性(白盒模型),这也是为什么说它是机器学习算法中最“友好”的一个原因。
2.随机森林
随机森林是一种强大的机器学习算法,属于集成学习方法的一种,由Leo Breiman在2001年提出。它通过构建大量决策树来进行分类或回归任务,并通过聚合这些树的预测结果来提高整体模型的准确性和鲁棒性。随机森林的"随机"体现在两个关键方面:一是在每棵树的训练过程中,从原始训练数据集中随机选择一部分数据点,即通过自助采样(bootstrap sampling)形成不同的数据子集;二是在每棵树的每个分裂节点上,并不是考虑所有可能的特征,而是随机选择一部分特征进行最佳分裂点的搜索。
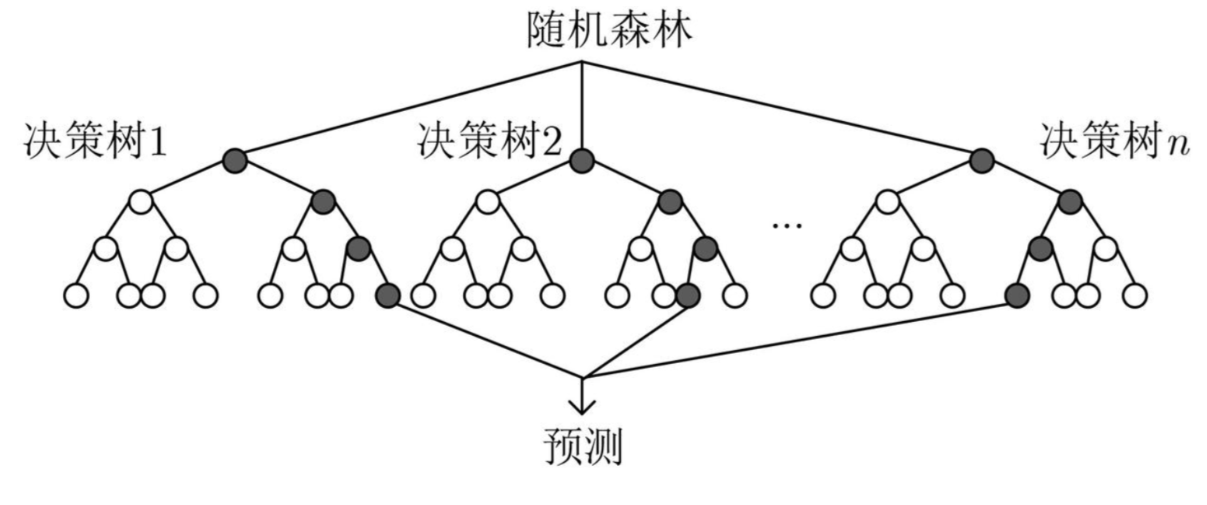
三.adaboost算法简介
1.感性认识
AdaBoost 说白了就是 “一群菜鸟凑一起干成大事” 的思路,用大白话讲就是这么个过程:
1. 先理解两个关键角色
- 弱分类器:能力很菜,比如只能勉强分辨 “苹果和梨”(正确率刚过 50%,比瞎猜好一点)。
- 强分类器:能力很强,能准确分辨各种水果,是由一堆弱分类器 “抱团” 形成的。
2. 核心逻辑:让弱分类器 “取长补短”
比如要做一个 “区分猫和狗” 的分类器,步骤大概是这样:
第一步:找第一个 “菜鸟”(弱分类器 1)
- 给所有训练样本(比如 100 张猫、100 张狗的图片)相同的 “关注度”(权重)。
- 让第一个弱分类器学,它可能只会看 “耳朵形状”,结果把 30 张狗误判成猫(正确率 70%)。
- 给这个弱分类器打个分(权重):正确率还行,给个中等分(比如 0.6)。
- 重点:那些被它分错的 30 张狗的图片,下次要让后面的分类器 “多看看”(把它们的权重提高)。
第二步:找第二个 “菜鸟”(弱分类器 2)
- 现在重点关注上一轮分错的 30 张狗的图片(权重高),其他图片权重低。
- 第二个弱分类器可能只会看 “尾巴长度”,这次它把大部分之前分错的狗认出来了,但可能又错了 20 张猫的图片。
- 给它也打个分:这次专攻了难认的样本,给个高分(比如 0.8)。
- 再调整权重:把这轮分错的 20 张猫的图片权重提高。
第三步:重复找 “菜鸟”
- 每一轮都让新的弱分类器去学上一轮分错的样本(因为这些样本权重高,相当于 “重点复习”)。
- 每个弱分类器都有自己的 “擅长点”(有的看耳朵,有的看尾巴,有的看体型),也有自己的分数(正确率高的分数高)。
第四步:凑成 “专家团”(强分类器)
- 当找了足够多的弱分类器(比如 10 个),就把它们的判断 “加权投票”:
- 分数高的弱分类器(比如 0.8 的那个)说话更算数,它的判断权重更大;
- 分数低的(比如 0.6 的)说话分量轻一点。
- 最后按 “多数票”(加权后)决定结果,比如大部分分类器说 “是狗”,那就判定为狗。
总结:AdaBoost 就是
让一群 “各有所长但能力一般” 的弱分类器,通过 “每次重点学之前搞错的内容”,最后把它们的意见按 “水平高低” 综合起来,变成一个厉害的强分类器。
就像考试:第一次复习错了 30 道题,第二次重点看这 30 道,又错了 20 道,第三次重点看这 20 道…… 最后把每次复习的心得按重要性综合起来,就能考高分了。
2.正式介绍
AdaBoost算法,简单来说,就是把很多个不是很强大的模型组合起来,形成一个非常强大的模型。在这个过程中,AdaBoost特别关注那些之前被错误分类的数据点,确保这些点在后续的训练中得到更多的注意,从而提高整体的学习效果。
- 首先,是初始化训练数据的权值分布D1。假设有N个训练样本数据,则每一个训练样本最开始时,都被赋予相同的权值:w1=1/N
- 然后,训练弱分类器hi。具体训练过程中是:如果某个训练样本点,被弱分类器hi准确地分类,那么在构造下一个训练集中,它对应的权值要减小(做对的题不用重点复习);相反,如果某个训练样本点被错误分类,那么它的权值就应该增大(做错的题要重点复习)。权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 最后,将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
- 换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
这里有几个点其实说的很抽象
“权重”:其实就是这个数据点的系数,权重越高,那么在下次迭代时会“得到更多关注”
“得到更多关注”,其实本质是影响的是损失函数,权重越高,在损失函数中所占比重越大,那么模型就会更加关注这个数据点(一旦被错误分类,那么会导致损失函数值加大很多,那么相应的模型也需要更多的调整以适应这个数据,根据损失函数调整的过程中其实就是对这个数据的关注)。
