卡尔曼滤波算法原理详解:核心公式、C 语言代码实现及电机控制 / 目标追踪应用
本文全面拆解卡尔曼滤波算法,从核心思想到落地应用,为工程开发与理论学习提供完整参考。首先明确卡尔曼滤波“融合预测与观测”的递归本质,详细分析其“高效实时处理、高斯假设下最优估计、多源信息融合”等优点,同时指出“线性高斯依赖、模型参数敏感、高维计算复杂”等局限性,帮读者精准判断算法适用场景。
卡尔曼滤波算法的核心思想是融合预测和观测,通过递归的方式,在存在不确定性的情况下,计算最优的估计。
1. 卡尔曼滤波的优缺点
优点:
- 高效递归:计算量小,只需当前时刻的估计和测量,无需保存大量历史数据,适合实时处理。
- 最优估计:在系统线性且噪声为高斯的假设下,能提供统计意义下的最优估计(最小方差估计)。
- 处理噪声:能有效处理系统和测量中的随机噪声。融合多源信息:天然适合多传感器数据融合,能综合不同传感器的优点,提供更鲁棒的估计。
局限性:
- 线性与高斯假设:标准的卡尔曼滤波要求系统动态模型和观测模型是线性的,且过程噪声和观测噪声均为高斯白噪声。实际系统常存在非线性。
- 模型依赖性:滤波效果严重依赖于系统模型(F, H)和噪声统计特性(Q, R)的准确性。这些参数若设置不当,会导致估计偏差甚至发散。
- 计算复杂度随状态维数增加:对于高维状态空间,矩阵运算的计算量会显著增加
2. 卡尔曼应用方向
由于卡尔曼滤波的计算量小,所以在实时性的场景下应用较为广泛。
| 应用领域 | 具体应用场景 | 卡尔曼滤波的作用 |
| 目标追踪 | 雷达、视频监控、无人驾驶中的车辆 / 行人跟踪 | 预测目标下一时刻位置,融合多传感器(如雷达、摄像头)数据,平滑轨迹,估计更准确的位置、速度、加速度。 |
| 电机控制与滤波 | 伺服电机、机器人关节电机、无人机旋翼控制(如 STM32 测电机速度) | 滤除编码器反馈信号中的噪声,更准确地估计电机转速和位置;结合电流传感器等,实现更精密的状态观测和控制。 |
| 导航与定位 | 无人机、自动驾驶汽车、机器人、手机导航 | 多传感器融合的核心算法。例如,融合 GPS(绝对位置但更新慢、有噪声)和 IMU(惯性测量单元,高频但误差累积)数据,提供连续、高精度的位置、速度和姿态估计。 |
| 信号处理与经济预测 | 去除信号中的噪声、股票价格预测、经济指标分析 | 从含噪声的时间序列数据中提取真实趋势,或基于历史数据进行短期预测。 |
| 航空航天 | 卫星轨道确定、导弹制导、飞行器姿态控制 | 估计飞行器的精确位置、速度和姿态,是导航和控制系统的重要组成部分。 |
3. 卡尔曼滤波实例展示
卡尔曼滤波计算量小、效果明显和无需保存历史数据,适合实时信号处理。下图为某次电机运转后,电机速度的原始图像和卡尔曼滤波后的曲线图(橘红色为滤波后曲线,蓝色为原始曲线)。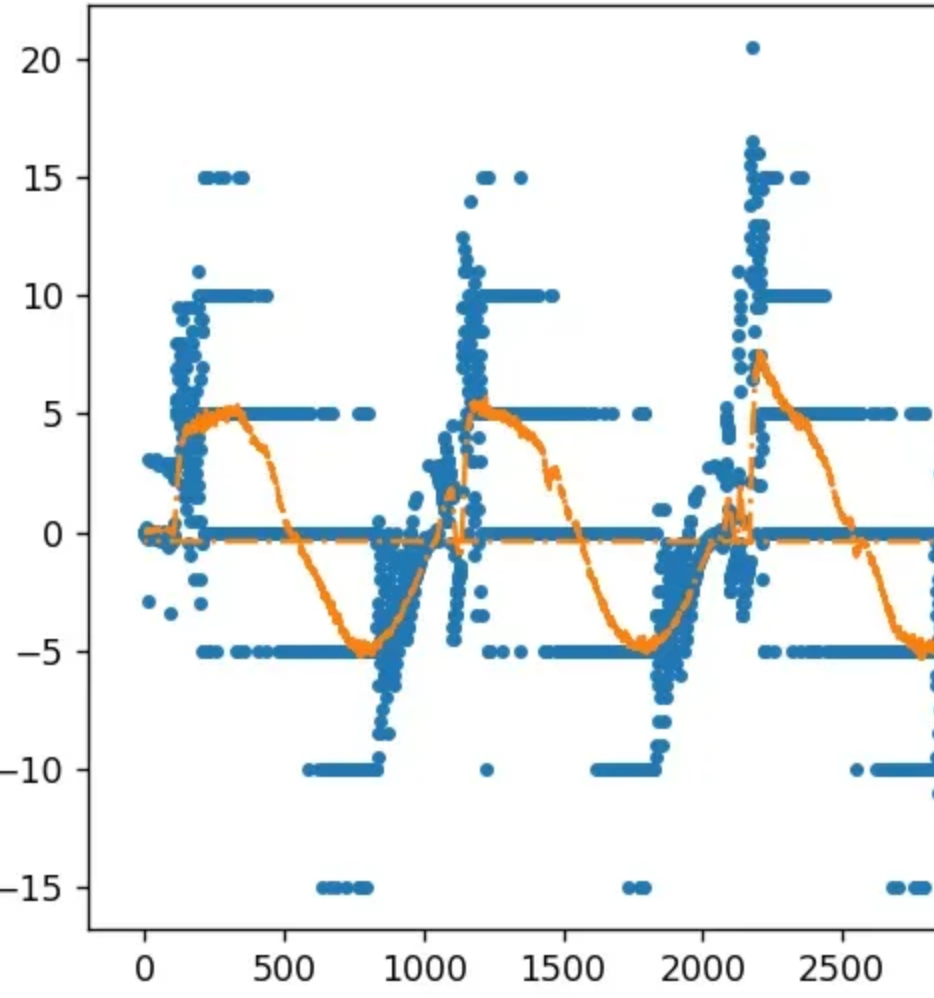
4. 卡尔曼滤波原理,由以下五个核心公式组成:
1. 状态方程预测
![]()
2. 误差协方差预测
![]()
3. 增益计算

4. 状态方程更新
![]()
5. 误差协方差更新
![]()
根据上述公式编写 C 语言代码如下:
float Kalman_Filter(Kalman* p,float dat)
{if(!p) return 0;p->X =p->A*p->X_last; p->P = p->A*p->P_last+p->Q; p->kg = p->P/(p->P+p->R); p->X_now = p->X+p->kg*(dat-p->X); p->P_now = (1-p->kg)*p->P; p->P_last = p->P_now;p->X_last = p->X_now;return p->X_now;
}
Kalman 结构体中变量解释:
A: 状态转移矩阵(或系数),表示状态如何随时间变化。
Q: 过程噪声协方差,表示系统模型的不确定性。
R: 观测噪声协方差,表示传感器测量的不确定性。
X_last: 上一时刻的后验状态估计 (k-1|k-1)。
P_last: 上一时刻的估计误差协方差 (k-1|k-1)。
X: 当前时刻的先验状态预测 (k|k-1)。
P: 当前时刻的预测误差协方差 (k|k-1)。
kg: 卡尔曼增益 (Kk),决定了我们更相信预测还是测量。
X_now: 当前时刻的后验状态估计 (k|k),即最终的滤波输出。
P_now: 当前时刻的估计误差协方差 (k|k)。
5. Kalman 滤波和 C 代码对应解释
(1)预测阶段 (Prediction)
继续阅读全文:卡尔曼滤波算法原理详解:核心公式、C 语言代码实现及电机控制 / 目标追踪应用
