当前位置：首页 > news >正文

《深入浅出统计学》学习笔记（二）

news 2025/11/2 8:08:33

前言

这篇博客是我在学习《深入浅出统计学》这本书时整理的个人笔记。《深入浅出统计学》作为一本经典的统计学入门书籍，内容由浅入深、案例丰富，全书共 15 章。考虑到知识点的连贯性和阅读体验，我计划将整本书的学习笔记分为 3 篇在 CSDN 上分享，每篇聚焦 5 个章节的内容，本篇便是系列笔记的第二篇，涵盖书中的第 6章到第 10 章。

六、排列与组合

1.独立、圆形、类别排位

2.排列、组合

七、几何、二项、泊松分布

1.几何分布

2.二项分布

3.泊松分布

八、正态分布的运用

1.连续数据、概率密度函数

2.正态分布、三步法计算法

九、再谈正态分布的运用

1.线性变换、独立观察结果

2.正态近似代替二项分布

3.正态近似代替泊松分布

十、统计抽样的运用

1.总体、样本、抽样偏倚

2.消失的咖啡销量推理

3.抽样方法分类与应用

结束语

在整理笔记的过程中，我会结合书中的核心内容，提炼重点概念、公式推导以及典型例题。为了更直观地呈现书本中的关键图表、例题解析和知识点框架，笔记里穿插了部分书本内容的截图，这些截图将与我的文字解读相互补充，帮助大家更好地理解统计学的基础原理。

由于是个人学习笔记，内容可能会带有一定的个人理解视角，若存在表述不够准确或遗漏的地方，欢迎大家在评论区留言指正。

注意：起初笔记是写在飞书上，现在是转化分享到csdn里，因此部分地方格式显示不全或看着不美观（如公式、图片等）

六、排列与组合

1.独立、圆形、类别排位

① 阶乘（独立排位）

指标定义：计算n个独立对象的排列方式数。n的阶乘写作n!，读作“n的阶乘”
计算公式：n！= n*(n-1)*(n-2)*...*3*2*1【注：0!=1，可理解为0个对象只1种排列方法】
指标性质：阶乘仅针对正整数，因此无法求负数或非整数的阶乘；只有当n=0或n=1时，阶乘结果为 1（奇数）,其余正整数的阶乘结果为偶数

② 圆形排位

核心逻辑：圆形排列中 “旋转后相同的排位视为同一情况”，需固定一个对象的位置以避免重复计算
计算公式：假设有n个位置，那么：
- 如果按照圆形排位（正常情况），那排位的结果数是： (n-1)!
- 如果考虑到把顺时针和逆时针排位视为同一种情况，那排位的结果数是： (n-1)!/2
- 如果考虑到绝对位置的话（即旋转后视为不同），那排位的结果数是： n!
案例分析：

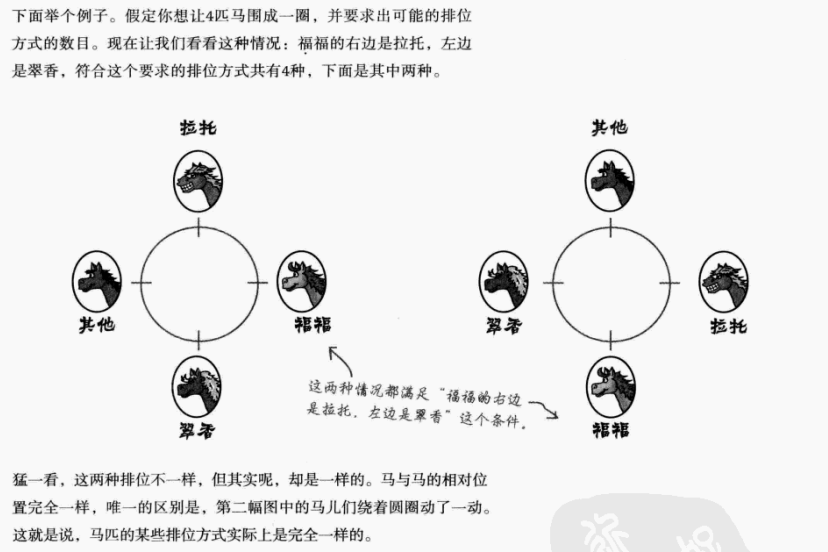
这一类问题该怎么解决呢？关键是把其中一匹马的位置固定下来，比如福福。只要福福站在某个位置上不动，就能计算其余3匹马的排位方式，这样就能避免重复计算，得出正确的结果。

假设福福固定，那它的左边可坐：拉托、其他、翠香三种可能；右边可坐除了左边外另外两种可能；对面就剩下一种可能，即求3的阶乘。可得出4个位置，如果按照圆形排位，那么排位的可能数是3！

③ 类别排位（同类对象排位）

核心逻辑：当对象存在类别划分（类内个体顺序不影响类别顺序）时，需用 “总独立排列数除以各类内部的排列数”。【按独立个体排位与按类别种类排位不是一回事】
计算公式：如果要为n个对象排位，其中包括第一类对象k个，第二类对象j个，第三类对象m个，则排位方式数目的计算式为 $\frac{n!}{k!j!m!}$
案例分析：假设ABC三个字母排序，将A、B划为一类，将C划分为一类，那现在按照类别排序有多少种可能？

① 看ABC三字母的排序一共有3!=6种可能，即ABC、ACB、BAC、BCA、CAB、CBA

② 由于把A、B划分为一类，那ABC和BAC是一样的（仅A、B内部顺序不同，类别顺序一致），同理ACB和BCA属于同一类排序，CAB和CBA也属于同一类排序；对于这类因类内个体顺序不同但类别顺序相同的情况，每一组只需保留一种即可，而 C 单独为一类，无类内个体顺序变化的问题

③ 通过筛选后，最后的结果只有ABC、ACB、CAB这三种可能，即按照类别排序有 3 种可能

④ 如果以上的例子利用公式计算则为\frac{3!}{2!1!}=\frac{6}{2*1}=3，其中3!代表ABC三种独立个体的排序可能数，2!代表AB这一类内部排序的可能，1!代表C这一类内部排序的可能，用总的独立个体排序除以内部的排序可能数

2.排列、组合

问题1：竞猜 10 匹马比赛的前三名（需明确名次顺序）

答：从 10 匹马中选 3 匹并按名次排序，第 1 名有 10 种选择，第 2 名需从剩余 9 匹中选（1 种选择），第 3 名需从剩余 8 匹中选（1 种选择），因此总排名方式为 10×9×8=720 种，最后的答案是1/720

问题2：竞猜 10 匹马比赛的前三名（无需明确名次顺序）

答：由于问题 1 的排列结果中，包含了同一组 3 匹马的不同名次顺序（如 “马 A 第 1、马 B 第 2、马 C 第 3” 与 “马 B 第 1、马 A 第 2、马 C 第 3”，本质是同一组 3 匹马），需剔除这些重复情况；因此总结果数目为排列数除以内部排列数，即10*8*7 / 3!=720/6=120种，最后的答案是1/120

通过观察以上两个问题，两者的区别就是前3名的是否考虑到位置的排序。如果需要考虑名称顺序，则为排列；如果不需要考虑名称顺序，则为组合。

类型	定义	公式	核心区别
排列 $^np_r$	从n个对象中选r个有序排列	$^np_r = \frac{n!}{(n-r)!}$	是否考虑 “元素的顺序（位置）”
组合 $^nC_r$	从n个对象中选r个无序选取	$^nC_r = \frac{n!}{r!(n-r)!}$	是否考虑 “元素的顺序（位置）”

七、几何、二项、泊松分布

1.几何分布

案例分析：查德是一名滑雪者，在任意一次试滑中(假定每一次试滑都是独立的)不出事故顺利抵达坡底的概率均为0.2。当他第1次试滑成功的概率是多少？第2次才成功的概率是多少？第r次才成功的概率是多少？【注意：当他获得首次成功后，就打算结束】
案例回答：因为事件是独立，且成功概率为0.2。那第一次成功概率为0.2；第二次成功概率为0.8*0.2；第三次成功概率为0.8*0.8*0.2......以此类推，可以得到第r次的成功概率为0.8^(r-1)*0.2。

若将0.8用q代替失败，将0.2用p代替成功，即得到{P(X=r)=q^{r-1}*p}，这个公式叫概率的几何分布

指标定义：描述 “取得第一次成功所需的试验次数” 的概率分布，公式为 ${P(X=r)=q^{r-1}*p}$ ，其中p为单次成功概率，q为失败概率（q=1-p）,可以写成 ${X - Geo(p)}$ 【为了在第r次试验时取得成功，首先要失败r-1次】

几何分布包含以下条件:

① 进行一系列相互独立的试验

② 每一次试验都既有成功的可能，也有失败的可能，且单次试验的成功概率相同（对立事件）

③ 为了取得第一次成功需要进行多少次试验

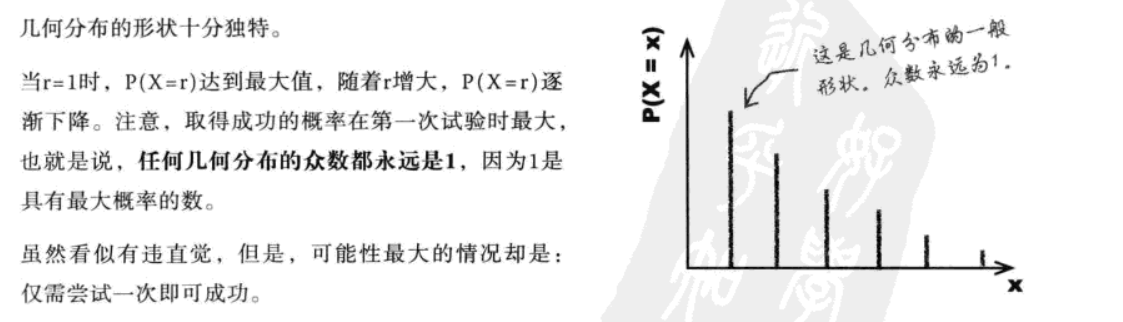
几何分布不等式

概率类型	概率含义	计算公式	公式解释
{P(X>r)}	取得第一次成功需要试验r次以上的概率	${P(X>r)} = q^r$	即表示前r次均失败【不需要确切地知道哪一次试验是成功的，只要知道试验次数必须大于r即可】
${P(X \leqslant r)}$	取得第一次成功需要试验r次或以下的概率	${P(X \leqslant r)} = 1 - q^r$	根据{P(X>r)} + {P(X \leqslant r)} =1推导而来。因两种概率类型是对立事件

几何分布总结

2.二项分布

案例分析：数学考试有3道选择题，每个选择题都有4个选项，每道选择题只有一个选项是正确的，请问答对0道、1道、2道、3道题的概率分别是多少？
案例回答：每道题4个选项，那每道题正确的概率为0.25，不正确为0.75。那答对0道是0.75^3；答对1道的P=0.75^2*0.25*3（乘以3是因为答对其中任意一题的情况有3种，即存在3种不同的组合）；答对2道的P=0.75*0.25^2*3（乘以3是因为答错其中任意一题的情况有3种，即存在3种不同的组合）；答对3道的P=0.25^3。若将0.75用q代替错误，将0.25用p代替正确，那么

P(X=0)=1*q^3*p^0；P(X=1)=3*q^2*p；P(X=2)=3*q*p^2；P(X=3)=1*p^3，这类问题为二项分布

指标定义：描述 “n次独立试验中成功r次” 的概率分布，公式为 ${P(X=r)=^nC_r*p^r*q^{n-r}}$ ，其中p为正确的概率，q为错误的概率（q=1-p）, $^nC_r = \frac{n!}{r!(n-r)!}$ ，可以写成 ${X-B(n,p)}$

二项分布包含以下条件:

① 进行一系列相互独立的试验

② 每一次试验都既有成功的可能，也有失败的可能，且单次试验的成功概率相同（对立事件）

③ 试验次数有限制

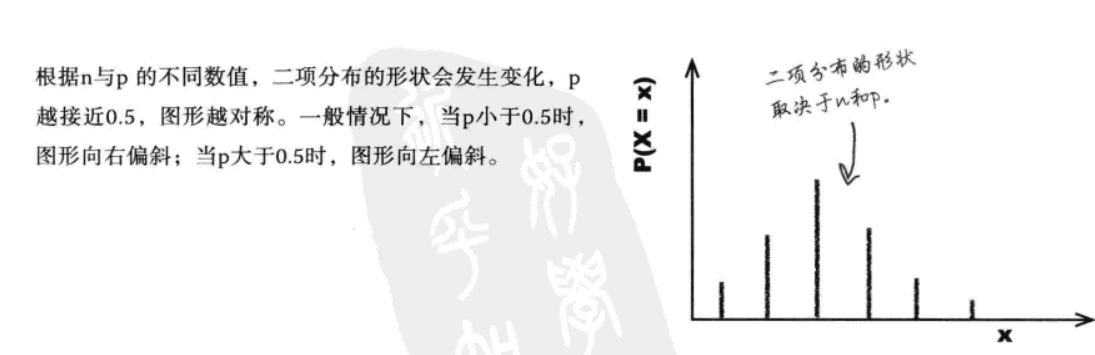
补充：几何分布是有众数的（值为1）。二项分布的众数需分情况判断：（众数是概率分布中概率最高的数值）

  ① 如果p为0.5且n为偶数，则众数为np

  ② 如果p为0.5且n为奇数，则该概率分布有两个众数，即位于np左右两侧的两个数值

  ③ 对于其他n值和p值，则需要通过反复试算的方法求众数，但一般都非常接近np

二项分布总结

几何分布和二项分布的区别：

相同点：二者处理的都是独立试验，每次试验都或是成功，或是失败

不同点：① 如果试验次数n固定，求成功一定次数的概率，则使用二项分布，如“n次试验中成功r次的概率”； ② 如果是在取得第一次成功之前需要试验多少次，无固定试验次数，则使用几何分布

3.泊松分布

案例分析：电影院下星期有大型促销，经理担心爆米花机故障影响活动 —— 已知机器每周平均故障 3.4 次，需算其下星期不故障的概率是多少？
案例回答：这个问题与之前遇到的情况有所不同。此前的问题多围绕 “一系列独立试验” 展开，而这次的是已知故障发生的平均几率，且故障本身属于随机出现的事件。面对这类 “特定区间内随机事件发生概率” 的问题，恰好可以借助泊松分布来分析

【请先看完“指标定义”后再看这段内容】根据泊松分布公式可知道问题的可写成{X-Po(3.4)}，那么下一周爆米花机不发生故障的概率为 $P(X=0)=\frac{e^{-\lambda}\lambda^r}{r!}=\frac{e^{-3.4}*3.4^0}{0!}=0.033$
指标定义：描述 “特定区间内随机事件发生次数” 的概率分布，公式为 ${P(X=r)=\frac{e^{-\lambda}\lambda^r}{r!}}$ ，其中 $\lambda$ 为区间内事件平均发生次数（ $\lambda$ 不可以为负数，因为负数是没有意义的），可写成 ${X-Po(\lambda)}$

【用 $\lambda$ $\lambda$ 代表泊松分布的均值，而不用u，是因为泊松分布的分布的参数、期望和方差全都相等，可以确保公正】

【泊松分布与二项、几何分布的区别：泊松分布不需要做一系列试验，它描述了事件在特定时间内的发生次数】

泊松分布包含以下条件:

① 单独事件在给定区间内随机、独立地发生，给定区间可以是时间或空间，例如可以是一个星期，也可以是一英里

② 已知该区间内的事件平均发生次数(或者叫做发生率)，且为有限数值。该事件平均发生次数通常用希腊字母入(lambda)表示

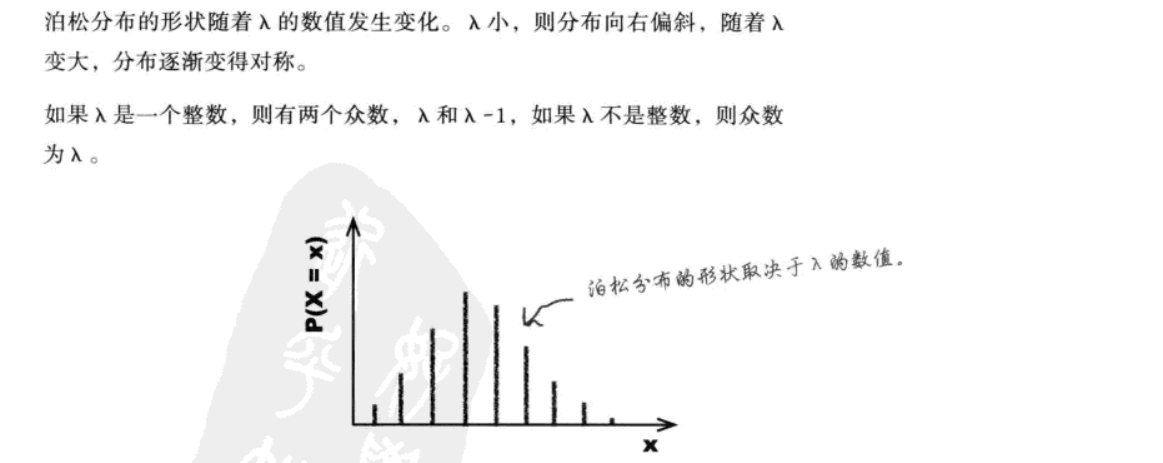
补充：泊松分布也有众数，也需分情况判断：

① 若\lambda是整数，则众数为\lambda和\lambda-1

② 若\lambda是非整数，则众数为\lambda的整数部分（即不大于\lambda的最大整数）【如案例中的众数为3】

组合泊松变量（多随机变量的线性组合）

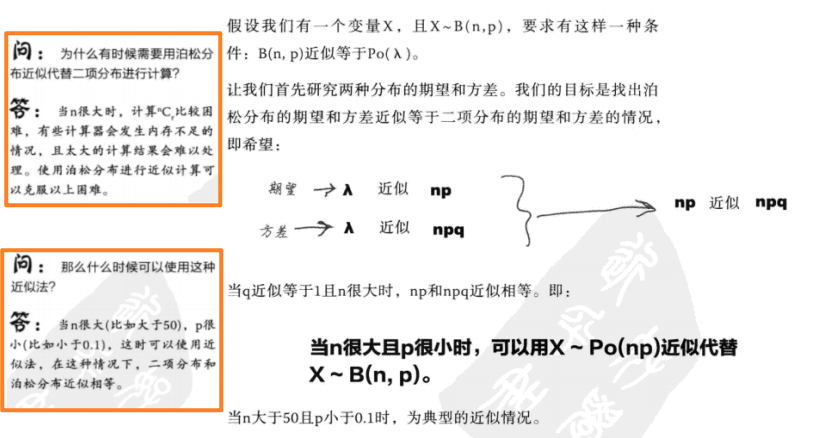
伪装下的泊松分布（近似代替二项分布）

泊松分布总结

几何、二项、泊松分布总结

几何分布、二项分布、泊松分布的对象皆属于：离散型随机分布

离散数据的特点：能取确切的数值，即数据由一个个单独的数值组成，每个数值都对应特定概率

八、正态分布的运用

1.连续数据、概率密度函数

案例分析：朱莉相亲时坚守一个时间观念，如果对方超过20分钟不来，那就会直接离开，那请问等5分钟以上的概率是多少?
案例回答：这是连续型随机变量，因为不可能列举每一个的时间节点（如4分钟10秒、4分钟11秒等情况），即时间可无限细分，因此是关注“数值范围的概率”

【请先看完“指标定义”表后再看这段内容】等5分钟以上的概率是5-20分钟区间的面积，即15/20 =0.75（高度相同）。因为函数f(x)的总面积等于1，那底(20)*高(f(x))=1，得到f(x)=0.05，那等5分钟以上，即15分钟的面积为15*0.05=0.75，即等5分钟以上的概率是0.75

指标定义	说明
连续数据	由测量得到，可取区间内任意确切数值（如丝线长度可测 10 英寸、10.1 英寸、10.01 英寸等），像 “平滑连绵的道路” 可无限细分
概率密度函数f(x)	描述连续随机变量的概率分布，通过面积表示概率；需关注 “数值范围的概率”，而非离散分布的 “特定数值概率”。
概率（连续分布）	连续随机变量在某一数值范围的概率等于其概率密度函数在该范围下方的面积，总面积（总概率）为 1

离散和连续的区别：

对于离散概率分布来说，关心的是取得一个特定数值的概率

对于连续概率分布来说，关心的是取得一个特定范国的概率

概率密度、概率密度函数和概率（连续分布）的区别：

概率密度：指出各种范围内的概率的大小（与第一章说到的“频数密度”十分相似），即一种表示概率的方法，但它并非概率本身【概率密度通过面积表示概率大小，而频数密度通过面积表示频数大小】

概率密度函数：图形中的 “曲线线条”，即f(x)

概率（连续分布）：图形中“曲线下某范围的面积”，即线条下方的一定数值范围内的面积

如果想求某一个精确的数值的概率，会是多少?

答：结果为0。以丝线长度为例：如果你需要一段长度正好等于10英寸的丝线，会出现什么局面？你会需要用一台高倍放大镜，以原子大小为精度，量出一段10英寸长的丝线。丝线的长度正好为10英寸”这个事件基本上不可能发生，也就是其概率为零。

2.正态分布、三步法计算法

① 正态分布 (别称：高斯分布)

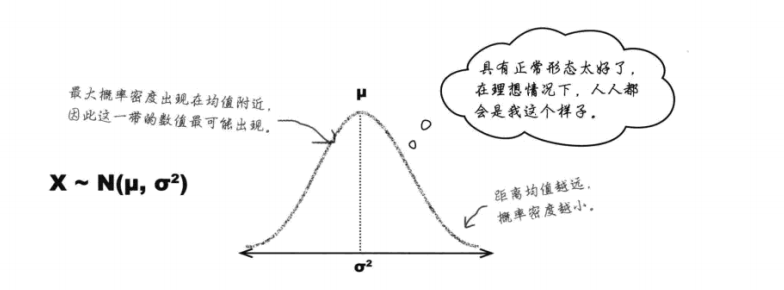
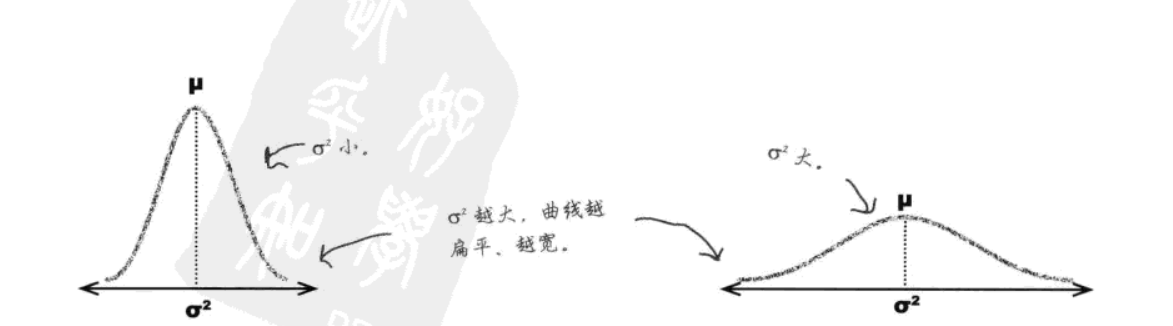
概率定义：正态分布是连续数据的“理想”模型，具有钟形对称曲线，中央部位的概率密度最大。越是偏离均值，概率密度减小。均值和中位数均位于中央，具有最大概率密度。（σ指出分散性）

如果一个连续随机变量X符合均值为u、标准差为σ的正态分布则通常写作X~N(μ，σ2)

分布特点：

[1] 无论把图形画多大（即σ2越大），概率密度永远不会等于0。概率密度会越来越接近0，但永远不会达到0。[2] 正态概率像处理其他连续概率分布一样，可通过计算分布曲线下方的面积求出概率。若想求出介于a和b之间的变量X的概率，则需求出曲线下方介于a点与b点之间的面积。

[3] 正态分布的众数、中位数均等于均值u（曲线最高点与面积二分点重合）

② 正态分布概率计算的三步法

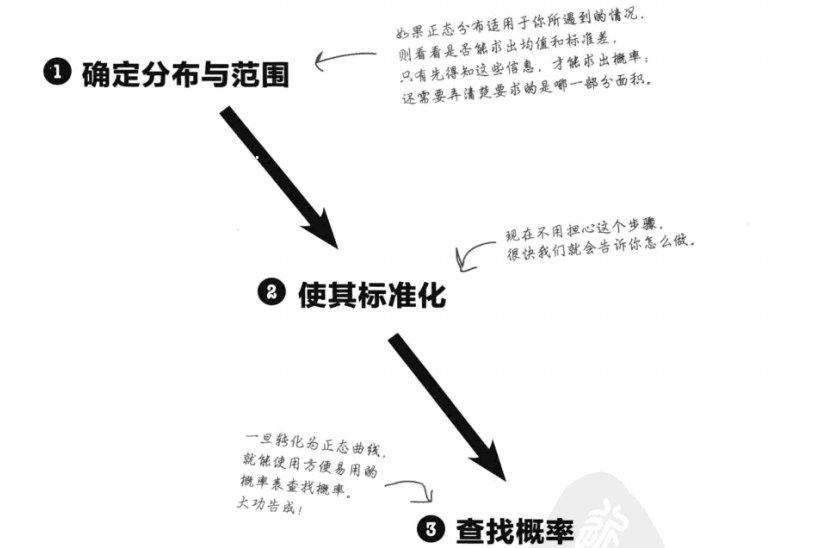
案例分析：以 “朱莉相亲对象身高” 为例，假设身高X-N(170,25)，求P(X > 180)

步骤	操作与计算
① 确定分布与范围	已知u = 170，σ = 5，需求P(X > 180)
② 标准化，转N(0,1)	标准分z= \frac{x-u}{\sigma}=\frac{180-170}{5}=2.00（结果保留2位小数），即Z-N(0,1)，需出P(Z>2.00)
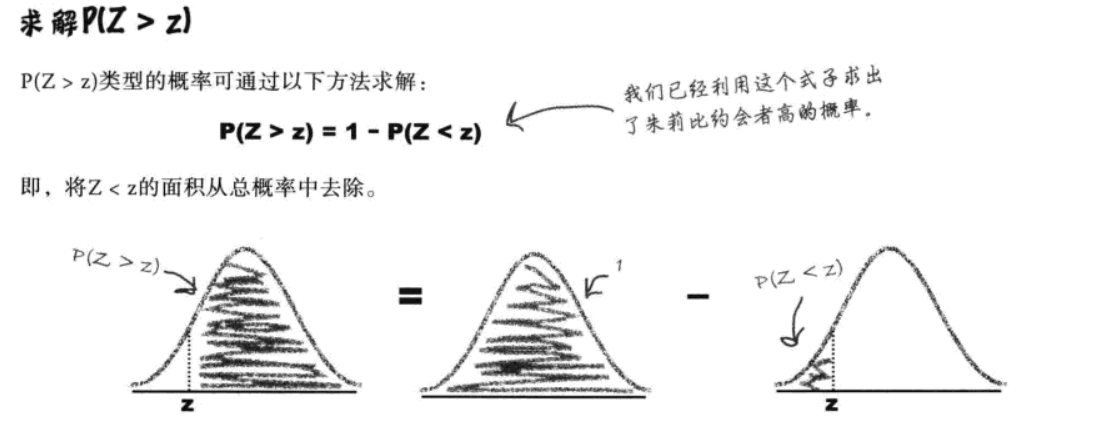
③ 查概率表计算	查标准正态分布表得(P(Z < 2.00) = 0.9772，故(P(Z > 2.00) = 1 - 0.9772 = 0.0228

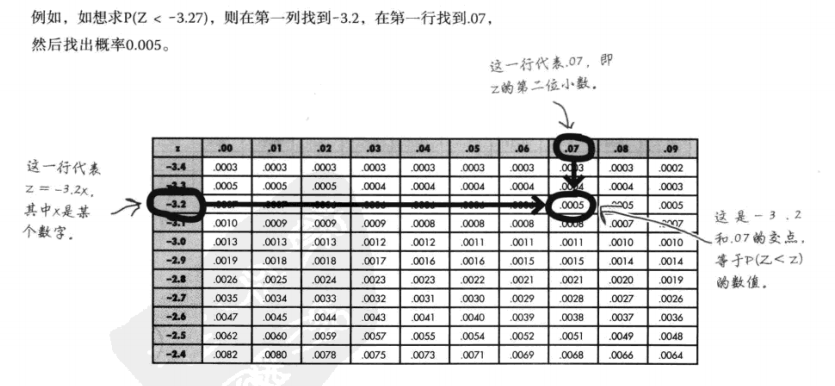
为何要标准化为N(0,1)：

概率表主要给出了N(0，1)分布的概率，无法为每一条正态分布曲线单独制定概率表。

u和σ2的可能取值无穷无尽，导致正态分布曲线的数量也无穷多，标准化可统一计算逻辑

九、再谈正态分布的运用

1.线性变换、独立观察结果

场景类型	条件与公式
独立正态变量的和 / 差	若X-N(u_x，σ_x^2)、Y-N(u_y，σ_y^2)且独立，则： X+Y-N(u_x+u_y，σ_x^2+σ_y^2)、X-Y-N(u_x-u_y，σ_x^2+σ_y^2)
单变量的线性变换	若X-N(u，σ^2)且a和b都是常数，则： aX+b-N(au+b，a^2σ^2)
独立观察结果的和	若X1、X2、X3、...、Xn是X-N(u，σ^2)的独立观察结果，则： X_1+X_2+...+X_n-N(nu，nσ^2)

场景类型

条件与公式

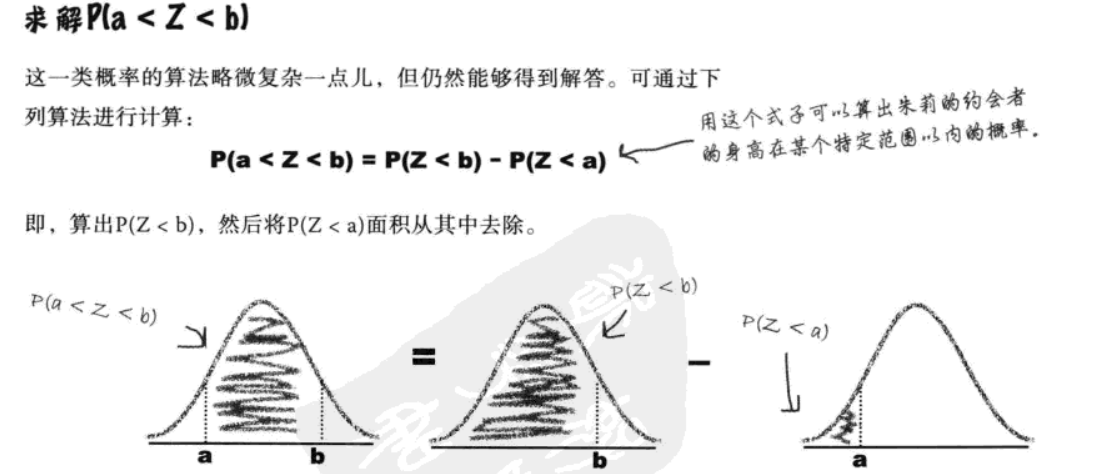
独立正态变量的和 / 差

若X-N(u_x，σ_x^2)、Y-N(u_y，σ_y^2)且独立，则：

X+Y-N(u_x+u_y，σ_x^2+σ_y^2)、X-Y-N(u_x-u_y，σ_x^2+σ_y^2)

单变量的线性变换

若X-N(u，σ^2)且a和b都是常数，则：

aX+b-N(au+b，a^2σ^2)

独立观察结果的和

若X1、X2、X3、...、Xn是X-N(u，σ^2)的独立观察结果，则：

X_1+X_2+...+X_n-N(nu，nσ^2)

2.正态近似代替二项分布

正态近似代替二项分布条件：如果X~B(n,p)，且np>5,nq>5，则可使用X~N(np，npq)近似代替二项分布
案例分析：

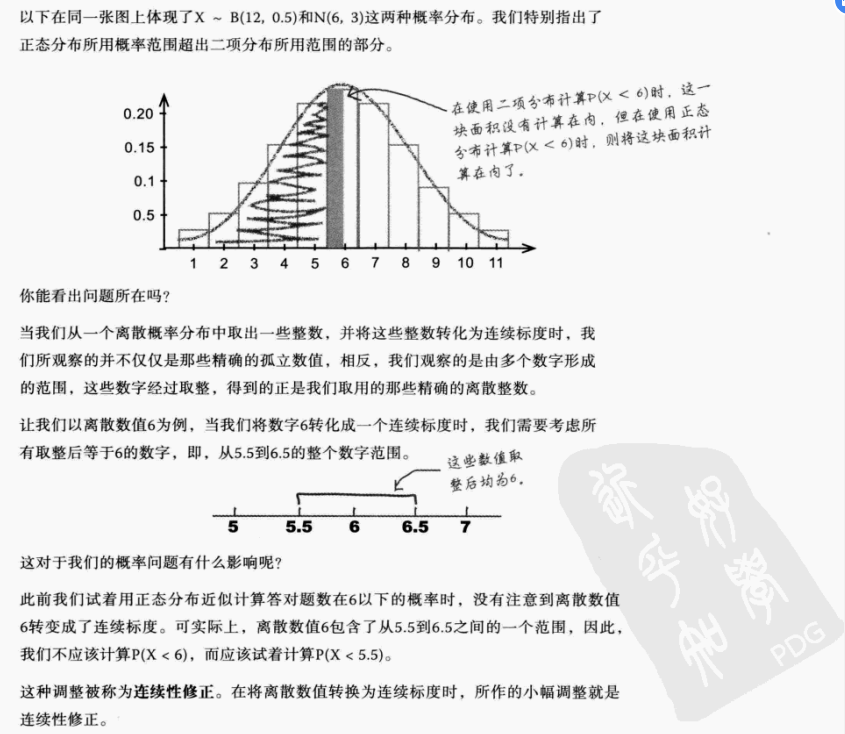
原因分析：

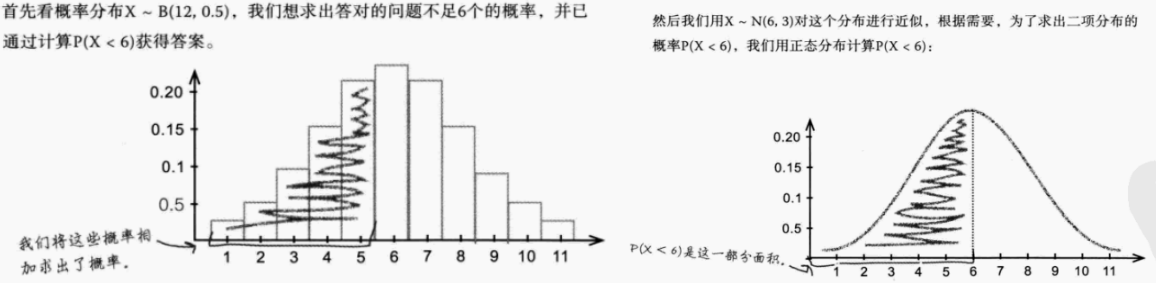
二项分布是离散分布，正态分布则是连续分布；需要进行连续性修正

连续性修正后：重新计算

记住:在用正态分布近似代替二项分布时，必须进行连续性修正！

正态分布和泊松分布都能作为二项分布的近似，该用哪一个?

这要看具体情况：

① 如果X~B(n,p)，当np>5且nq>5时，则使用正态分布近似代替二项分布

② 如果n>50且p<0.1，则可以使用泊松分布近似代替二项分布

连续性修正规则（含练习）：

概率类型	修正方式
P(X \leq a)	计算P(X < a + 0.5)
P(X \geq b)	计算P(X > b - 0.5)
P(a \leq X \leq b)	计算P(a - 0.5 < X < b + 0.5)

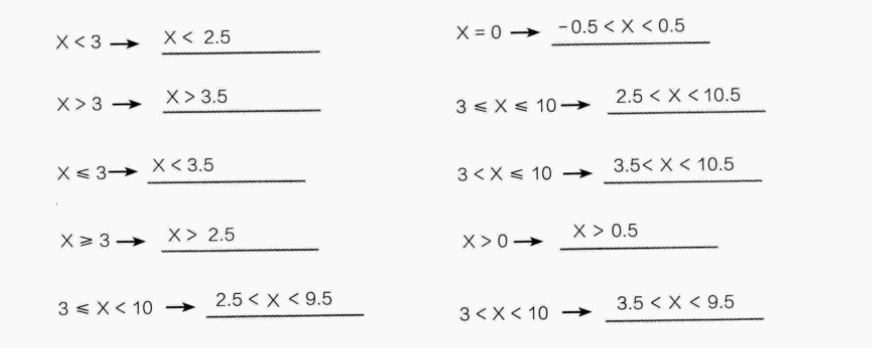
3.正态近似代替泊松分布

正态近似代替泊松分布条件：如果X~Po(入)且入>15，则可用x~N(入,入)进行近似
案例分析：

记住:在用正态分布近似代替泊松分布时，必须进行连续性修正！

二项分布和泊松分布都可以用正态分布近似表示，那么几何分布可以吗?

之所以可以用正态分布近似代替二项分布和泊松分布，是因为在某些特定情况下，这两种分布与正态分布具有相同的形状

而几何分布呢，它永远也不会和正态分布外形相似，因此正态分布绝不能有效地近似代替几何分布

本章小结

十、统计抽样的运用

1.总体、样本、抽样偏倚

概念定义：

概念	说明	案例
总体	需研究的整个群体（所有对象）。当总体数量很大，或者说无穷无尽时，就不可能对每一个对象进行研究	某中学初三年级共有 500 名学生，要研究该年级学生的数学成绩，初三年级全体 500 名学生就是总体
样本	从总体中选取的一部分对象，用于代表总体进行研究	从初三年级 500 名学生中随机抽取 50 名学生的数学成绩进行分析，这 50 名学生的数学成绩就是样本
抽样偏倚	样本无法客观反映总体的特性，会导致对总体的错误判断
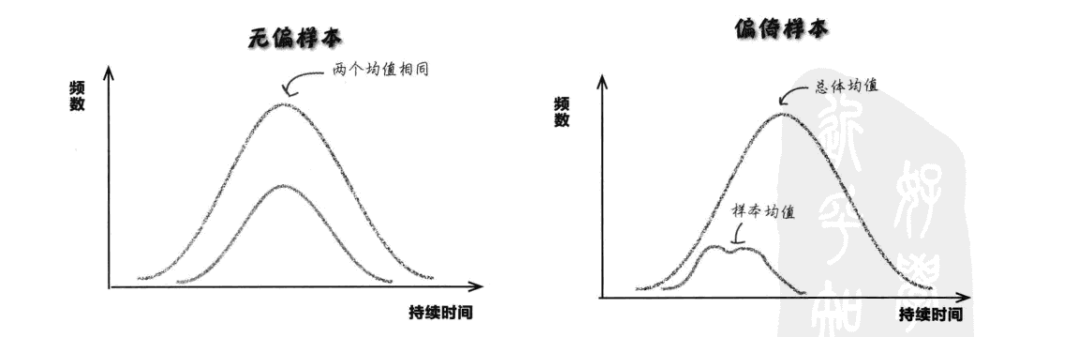
无偏样本	指能客观反映总体特性的样本，其分布形状、均值等特征与总体高度相似	从中学初三年级 500 名学生中，通过简单随机抽样抽取 50 名学生的数学成绩。若这 50 名学生的成绩均值、分数分布（如高分段、低分段占比）与全年级 500 名学生的成绩特征几乎一致，那么这个样本就是无偏样本
偏倚样本	指无法客观反映总体特性的样本，其特征与总体存在明显偏差	同样是抽取 50 名学生，但只选择了数学竞赛班的学生。这些学生的数学成绩普遍偏高，均值远高于全年级平均水平，分数分布也集中在高分段 —— 这样的样本就是偏倚样本，用它来推断全年级成绩会得出错误结论

抽样方法核心：构建优质样本的关键在于选取与总体高度契合的样本。若样本具备代表性，即其特性与总体极为相似，便可通过样本推断总体的特征。需注意，若使用具有误导性的样本，会导致对总体的判断出现错误
设计样本步骤：① 确定目标总体 → ② 确定抽样单位 → ③ 确定抽样空间
偏倚的成因与规避：

偏倚原因	说明	案例（统计邦健身俱乐部调查）
抽样空间不全	抽样空间未包含总体所有对象	客户花名册遗漏了部分新客户
抽样单位错误	选择的抽样单位不符合研究目标	若要研究 “每盒巧克力的品质”，抽样单位应为 “一盒” 而非 “一块”
样本选取不全	抽样单位未实际参与样本（如问卷无回应）	发送问卷后，只有年轻客户回复
问题设计不当	问卷问题带有引导性或排他性	问 “我们的设施是不是全市最好的？”
缺乏随机性	抽样时主观排除部分对象	调查时避开行色匆匆的客户

案例分析：

2.消失的咖啡销量推理

3.抽样方法分类与应用

抽样方法的定义

抽样方法	定义与操作	案例与特点
简单随机抽样	从总体中随机选取样本，所有可能的样本被选中的概率相同分为重复抽样（抽样单位放回）和不重复抽样（抽样单位不放回）	- 重复抽样：街头随机采访行人(可能重复采访同一人) - 不重复抽样：检验口香糖球(尝过的糖球不放回)
分层抽样	将总体按特征划分为 “层”（每层内部特性相似，层间特性不同），再对每层进行简单随机抽样	把口香糖按颜色分层（红、黄、绿等），再从每层按比例抽取
整群抽样	将总体划分为 “群”（群间特性相似，群内包含多种特性），先随机选取群，再对选中的群进行全面调查	按盒抽取口香糖（每盒为一个群，选中后检验整盒糖球）
系统抽样	将总体按顺序排列，每隔k个单位选取一个样本	客户花名册中每 10 个客户抽取 1 个
抽签	将抽样空间中每个成员的名称或编号写在纸条或球上，全部放入容器后随机抽取指定数量的样本单位	班级选代表时，把所有同学的名字写在纸条上放入盒子，随机抽取 3 张，被抽中的同学即为样本
随机编号生成器	为抽样空间的每个成员编制唯一编号，生成一组随机编号后，抽取编号对应的成员作为样本【确保每个编号的生成机会相同，从而避免偏倚】	统计某小区居民满意度时，给每户居民编一个编号，用随机数生成器生成 20 个编号，对应编号的居民组成样本

分层抽样与整群抽样的区别

维度	分层抽样	整群抽样
划分逻辑	层内特性相似，层间特性不同	群间特性相似，群内特性多样
抽样操作	对每层进行简单随机抽样	先随机选群，再调查群内对象
案例对比	按 “颜色” 分层抽口香糖（每层颜色单一）	按 “盒” 分群抽口香糖（每盒包含多种颜色）