机器学习日报10

摘要

今天学习了处理倾斜数据集时的评估指标问题。当正负样本比例严重失衡时，准确率会失去参考价值，比如在罕见病诊断中，总是预测"无病"也能获得高准确率。为此引入了精确率和召回率两个指标：精确率关注"预测为真的案例中有多少确实为真"，召回率关注"实际为真的案例中被预测出来的比例"。这两个指标通常存在权衡关系，通过调整分类阈值可以平衡二者。最后还学习了F1分数，它能自动综合精确率和召回率，帮助我们选择最佳模型。

Abstract

Today’s lesson focused on evaluation metrics for skewed datasets. When dealing with imbalanced classes (e.g., rare disease diagnosis), accuracy becomes misleading. We introduced precision and recall as more meaningful metrics - precision measures the accuracy of positive predictions, while recall measures the ability to find all positive instances. These two metrics typically involve a trade-off that can be managed by adjusting the classification threshold. The F1 score was presented as a harmonic mean of precision and recall that automatically balances both concerns for model selection.

一、倾斜数据集的误差指标

如果我们正在开发一个机器学习应用程序，而且正反例的比例失衡，远非50-50那么通常的错误度量标准，如准确率就不会那么有效，让我们从一个例子开始

假设我们正在训练一个二分类器，根据实验室测试或其他病人的数据来检测一种罕见的疾病，所以如果疾病存在y=1，否则y=0，假设我们发现测试集上的错误率是1%，所以我们有99%的正确诊断率，这看起来是一个很好的结果，但事实证明，如果这是罕见疾病，所以y=1的情况非常少，那么这可能并不像听起来那么令人印象深刻，具体来说，如果这是罕见疾病，如果我们的人群中只有0.5%的病人有这种病，那么如果我们写了一个程序，只输出y=0，它每次都预测y=0,这个非常简单，甚至是非学习的算法，它实际上会有99.5%的准确率或0.5%的错误率，所以这个非常笨的算法优于我们的学习算法，它有1%的错误率，远超过0.5%的错误率，但是我认为一个只输出y=0的软件并不是一个非常有用的诊断工具，这实际上意味着我们无法判断1%的错误率到底是好结果还是坏结果，特别是，如果我们有一个算法达到99.5%的准确率，另一个达到99.2%的准确率，再有一个达到99.6%的准确率，很难知道哪一个实际上是最好的算法，因为如果我们有一个算法达到0.5%的错误率，1%的错误率，还有1.2%的错误率，很有可能错误率最低的算法可能并不是特别有用的预测，比如这个总是预测y =0，永远不会诊断任何患者有这种疾病，很可能一个错误率为1%的算法，但至少能够诊断出一些患者患有这种疾病，会比总是输出y等于0的算法更有用，在处理数据集不平衡的问题时，我们通常使用一个不同的错误指标，而不是仅仅用分类错误来判断我们的学习效果

1、精确率和错误率

特别是一对常见的错误指标是错误指标是精确率和召回率，现在让我们画一个2X2的矩阵

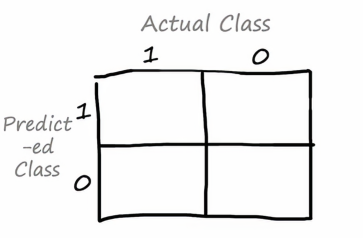
我们可以看到，在上面我们写的是实际类别，而左边是模型预测的类别，比如左上角的矩阵格代表的是模型预测为1并且实际上确实也为1的病人，说明我们的模型预测是成功的，为了评估我们的算法在交叉验证集上或测试集上的性能，我们将实际类别为1且预测类别为1的实例数量，假设100个交叉验证示例，其中15个示例是学习算法预测为1并且实际标签也为1，我们把剩下的情况填入这个矩阵当中

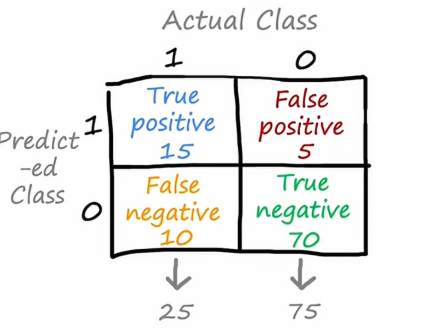
你可能会注意到，我用了四种不同的颜色来表示单元格中的四个情况，实际上，我们还需要给这四个单元格命名，当实际类别为1且预测类别为1时，因为我们预测的是正确的且标签值为1，我们称之为真正例，而右下角这个绿色数字，我们称为真负例，右上角称为假正例，因为我们预测的是1但实际上它的标签为0，同理，左下角我们称之为假负例

在明确了每个单元格的属性之后，我们就可以着手计算精准度和召回率了，学习算法的精确度计算，在我们所有预测y=1的患者中，有多少实际上患有罕见疾病，换句话说，精确度定义为真正例的数量除以被模型预测为正例的数量，另一种写这个公式的方法是用真理正例除以真正例加上假正例，如下图所示

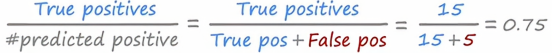
因此我们可以说，这个算法的精确度为75%，因为所有预测为正的例子中，在所有它认为患有这种罕见疾病的患者中它有75%的准确率

第二个有用的指标是召回率，召回率解决的问题是，在所有实际患有这种罕见病的患者中，我们正确检测出患有这种疾病的比例是多少，所以召回率被定义为真正例的数量除以实际正例的数量，我们也可以把它写成真正例的数量除以实际正例的数量，如下图所示：

所以这个学习算法的精准度是0.75而召回率是0.6，注意到它能帮助我们检测一个学习算法是否总输出y = 0，因为如果它总是预测为0，那么这两个数量的分子都为0，也就是说它没有真正例，召回率指标特别能帮助我们检测学习算法是否总是预测为0，因为如果总是为0，那么说明模型不会预测正例，这是不实用不现实的

总的来说，计算精确度和召回率使我们更容易发现一个算法是否相对合理地准确，当它判断患者有疾病的时候，患者真的有疾病的概率很大，同时，确保它帮助诊断的一定比例的患者确实患有疾病，例如这个例子中找到60%的患者，查看精确度和召回率并确保这两个数字都比较高，希望这能让我们确信我们的学习算法确实有用，所以当我们有偏斜类或一个稀有类别需要检测时，精确度和召回率会帮助判断我们的学习算法是否做出了好的预测或有用的预测

二、精确率与召回率的权衡

在理想情况下，我们希望学习算法具有高精确度和高召回率，高精度意味着如果它诊断出某人患有这种罕见疾病，很可能这个患者确实患有这种疾病，并且这是一个准确的诊断，高召回率意味着如果有患者患有这个罕见疾病，算法可能会正确识别他们确实患有这种疾病，在实际情况下，召回率和精确率常常存在这种权衡，在本节中，我们会学习如何在权衡中选择一个好的点

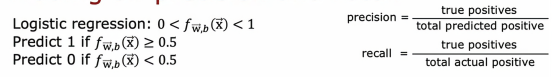
回忆一下我们上节所说的召回率和精确率，精确率是将真正例数除以预测为正的总数，召回率是将真正例数除以实际正例的总数，如果我们使用的是逻辑回归来进行预测，那么逻辑回归模型，将输出介于0和1之间的数值，我们通常会在0.5处对逻辑回归输出进行阈值处理，如果f(x)大于或等于0.5，那么我们预测为1，反之我们预测为0，但现在我们假设我们想预测y = 1，因为这个罕见病需要使用很先进的仪器并且吃的药是很贵的，那么这种情况下，除非我们很有把握，不然我们偏向于该患者没有患这种罕见病，在这种情况下，我们可能会选择设置一个更高的阈值，只有当f(x)大于或等于0.7时才预测y为1，所以这就是说我们只有在至少70%确定的情况下，才预测为y=1，所以这个数字也为0.7，因为这取决于你预测的数字是大于等于还是小于这个数字，通过提高这个阈值，这意味着精确度会提高，因为当我们预测为1的时候，我们更有把握确定它是正确的例子，但是召回率会变低，

因此，每当我们预测一个病人患有疾病时，我们很可能是对的，这样会给我们一个非常高的精确度，另一方面，假设我们想避免漏诊太多这种罕见疾病的病例，那么我们可以降低这个阈值，比如设定为0.3，在这种情况下，只要我们认为患病的概率高于百分之30，那么就认为这个病人患有这个罕见病，这样召回率会得到提升，但是精确度会有所下降

所以通过合理选择这个阈值，我们可以根据现实情况的不同选择不同的阈值进而指定合理的判断模型，现在让我们来绘制一下它们之间的关系，如果我们设置一个非常高的阈值，那么最终会得到一个高精确率但较低的召回率，当我们降低这个阈值，那么精确率会降低，召回率会逐步上升，这样我们就会得到一个精确率和召回率的曲线，如下图所示

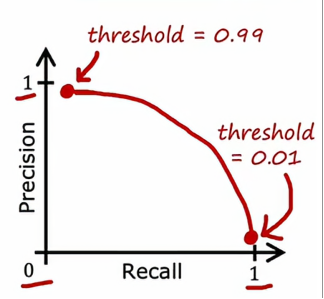
通过绘制这个曲线，我们可以找到召回率和精确率两者的平衡点，请注意，选择阈值并不是我们可以通过交叉验证真正进行的事情，因为我们需要自己来指定最佳点，手动选择阈值以权衡精准率和召回率将是我们最终会做的事情

1、 F1分数

事实证明，如果我们想自动权衡精准率和召回率，而不是自己手动去做，有一个叫做F1分数的指标，它有时用来被自动结合精确率和召回率，如下图所示

我们可以看到，如果按照我们惯性思维，我们一般想用平均数来衡量一个指标，那么我们看计算上图三个算法之后的平均值，我们可以看到，第三个算法貌似是最好的，至少我们从平均数这个指标来看，它是最高的，但是我们发现，第三个算法的精准度很差很差，低至0.02，这样对于一个患病检查的模型来说，0.02的精确度确实有点很难令人信服，所以，让我们看一下计算了F1分数之后的数值

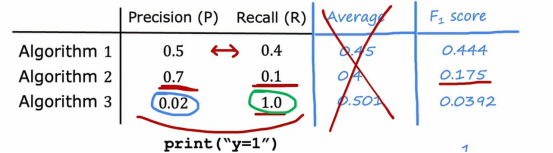
我们看到，算法1的F1分数为0.444，是最高的，那么我们看向精确率和召回率，它们确实是差别不大！一个是0.5，一个是0.4，确实相差并不是很大，所以通过F1分数这个概念配合上面说的那些图，我们可以很好的选择召回率和精确率的一个平衡点

总结

今天的学习让我明白了在数据不平衡时如何正确评估模型。之前只知道准确率，现在认识到在罕见病诊断这类场景中，精确率和召回率才是更合理的评估标准。通过那个2×2的混淆矩阵，我清楚了真正例、假正例这些概念的计算方式。最有启发的是精确率与召回率的权衡关系：提高阈值会让预测更谨慎（精确率上升但召回率下降），降低阈值则会更敏感（召回率上升但精确率下降）。F1分数的引入很巧妙，它不像简单平均那样会被极端值误导，而是通过调和平均数找到平衡点。这些知识让我以后面对倾斜数据集时有了正确的评估思路，不会再被表面的高准确率所迷惑。