《人工智能基础》[算法篇3]:决策树
什么是决策树?
在生活中,我们常常面临各种决策场景。比如周末决定是否出门游玩,会先看天气如何,如果天气晴朗,再考虑是否有朋友一起,接着考虑交通是否便利等因素,逐步做出最终决策。这个思考过程,其实就蕴含着决策树算法的基本思想。
决策树算法是一种基于树形结构的有监督学习算法 ,主要用于分类和回归任务。它的核心原理是通过对数据集进行递归分割,根据样本的特征值构建一系列的决策规则,从而对新数据进行分类或预测。
决策树相关概念
信息熵:信息熵是决策树中用来度量数据混乱程度的指标,熵越小,数据越纯,越适合作为分类节点
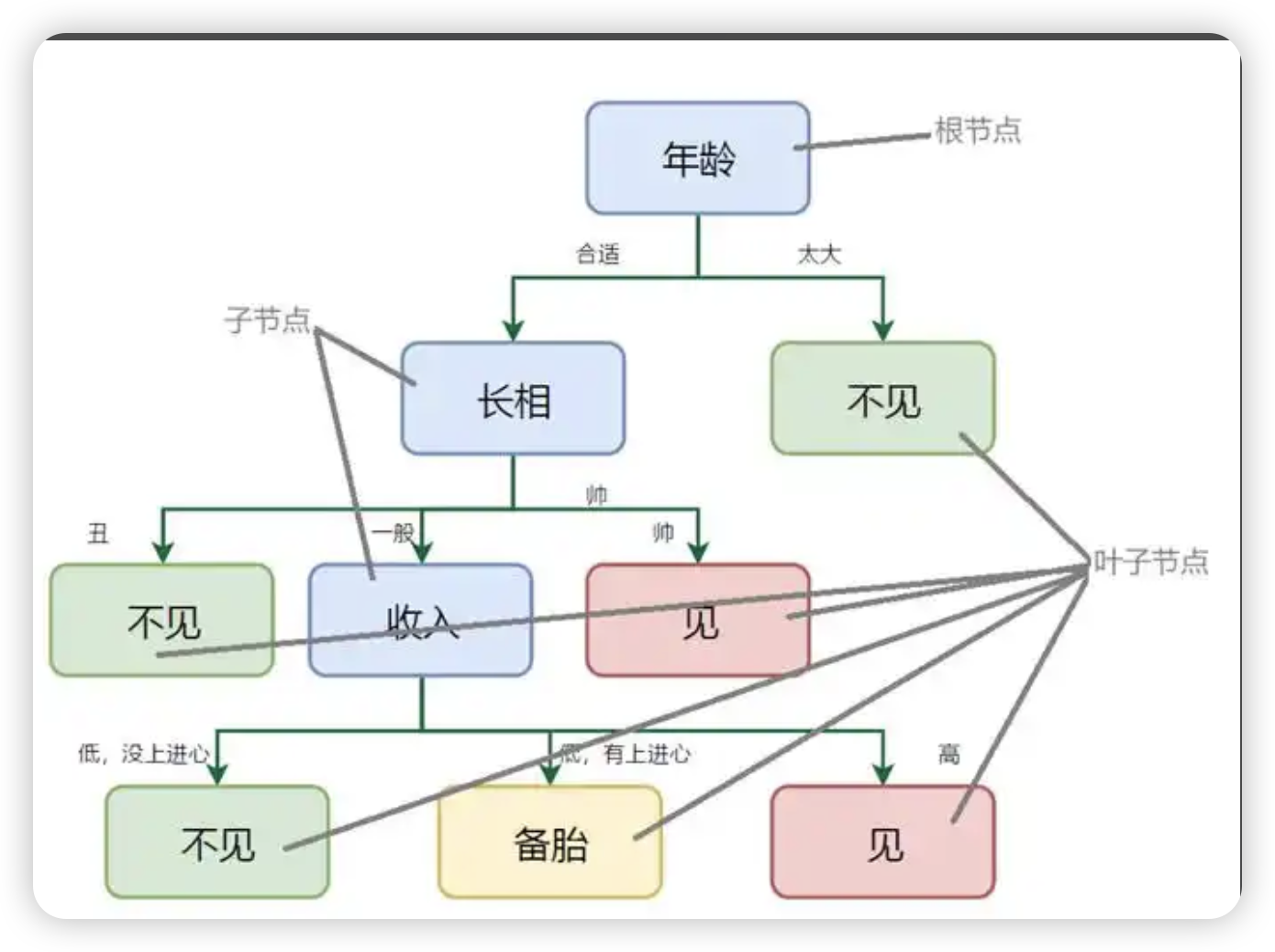
决策树包含三种结点:根结点(树的起点,包含全部数据)、内部结点(对特征进行判断和分支)和叶结点(最终的决策结果)
根节点:它是决策树的起始点,包含了整个样本集,就像树干是树生长的起点
内部节点:每个内部节点代表一个特征属性上的测试条件,比如上面决定是否出门游玩例子中的 “天气是否晴朗”,它决定了数据应该沿着哪条分支继续向下传递
叶节点:也称终端节点,是树的末端节点,不再有子节点,代表了最终的决策结果,如 “出门游玩” 或 “不出门游玩”
分支:连接着各个节点,表示从一个测试条件到另一个测试条件或结果之间的转移,每个分支对应一个特征属性的取值。例如从 “天气是否晴朗” 这个内部节点延伸出 “晴朗” 和 “不晴朗” 两条分支
决策树算法的优缺点
| 优点 | 缺点 |
|---|---|
| 1. 易于理解和解释:模型可以可视化,最终的决策逻辑(如果-那么规则)非常直观,即使非专业人士也能理解 | 1. 容易过拟合:树可能会生长得过于复杂,捕捉到训练数据中的噪声和特殊细节,导致在未知数据上表现不佳 |
| 2. 需要的数据预处理较少:不需要对数据进行标准化或归一化,对缺失值不敏感,能够处理数值和类别数据 | 2. 不稳定:训练数据的微小变化可能导致生成一棵完全不同的树,因为分裂节点时特征选择的路径可能改变 |
| 3. 支持多种数据类型:可以同时处理数值型特征(如年龄、收入)和类别型特征(如性别、城市) | 3. 容易产生偏差:如果某些特征占主导地位,树会倾向于使用它们,导致有偏的树 |
| 4. 模型是非参数的:没有对数据的基础分布做出任何假设,可以自由地学习任何数据形式 | 4. 可能创建过于复杂的树:不加控制地生长会导致模型复杂化,可解释性下降,并引发过拟合 |
| 5. 可以用于特征选择:通过观察哪些特征被用在树的顶部节点,可以判断特征的重要性 | 5. 难以学习复杂关系:对于如“异或”问题等复杂的线性或非线性关系,决策树难以有效建模,需要非常复杂的树 |
| 6. 计算复杂度相对较低:预测新样本的速度非常快,只需要从根节点走到叶子节点即可 | 6. 贪心算法的局限性:构建树时采用局部最优的贪心策略(在每个节点选择最佳分裂),无法保证返回全局最优的决策树 |
可通过剪枝、设置树的最大深度、设置叶子节点的最小样本数等方法来缓解。同时,通过集成学习方法(如随机森林、梯度提升树)将多棵决策树组合起来,可以极大地克服单棵决策树的不稳定性和过拟合问题。
决策树的核心在于可解释性和性能之间的权衡。一棵简单的小树易于解释但可能欠拟合;一棵复杂的大树可能性能更好但难以解释且容易过拟合。
决策树的适用场景
决策树适用于需要清晰解释因果关系、处理混合类型数据(数值与类别),且追求快速建模与结果可解释的分类或回归任务,如客户流失预测、信用风险评估等场景。
需求可解释性时 当模型需要向业务方、管理层或客户提供清晰、直观的决策逻辑时,决策树的“如果-那么”规则是最佳选择
处理混合数据类型时 数据集中同时包含数值型(如价格)和类别型(如颜色)特征,无需繁琐的预处理即可直接使用
探索性数据分析和特征识别 通过观察树的结构,可以快速识别出哪些特征对预测结果最重要,常用于初步数据洞察
对计算资源要求不高的场景 预测阶段速度极快,适合需要快速响应的应用场景
深入了解决策树原理
1、核心思想
决策树的根本思想是“分而治之”(Divide and Conquer)。它试图通过提出一系列“if-then”的规则性问题,将庞大的、复杂的原始数据集递归地分割成更小、更纯净的子集。
打个比方:医生诊断病人
医生会以 “患者是否感冒” 为最终目标,从最关键的症状开始,逐步向下拆分判断。
根节点(第一层判断):优先看最典型的症状,比如 “是否发烧(体温≥37.3℃)”。这是区分普通感冒与其他疾病(如过敏)的关键第一步。
内部节点(第二层判断):基于第一层结果继续拆分。
若 “发烧”:进一步判断 “是否伴随肌肉酸痛、乏力”,区分是普通感冒还是流感。
若 “不发烧”:判断 “是否有鼻塞、流涕、咽痛”,排除鼻炎、咽炎等其他上呼吸道问题。
叶节点(最终结论):经过多层判断后,得出具体结论,比如 “普通病毒性感冒”“甲型流感”“细菌性感冒”,并对应 “多休息喝水”“服用抗病毒药物”“使用抗生素” 等治疗方案。
2、决策树的划分依据
决策树算法中的关键问题是如何选择最佳的分裂准则,常见的分裂准则包括信息增益、基尼系数和均方差等。信息增益是一种常用的分裂准则,用于度量特征对样本集合纯度的提升程度。基尼系数是另一种常用的分裂准则,用于度量样本集合的不纯度。
构建过程的关键在于:在每个节点上,选择哪个特征以及该特征的哪个值进行分割,才能最有效地“纯化”数据?
2.1、信息熵增益分裂法
2.1.1、信息熵
定义:衡量一个数据集的不确定性(混乱程度) 的指标
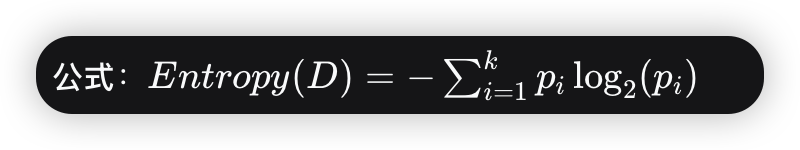
D:当前数据集
k:类别数(如:是/否)
pi:数据集中第 i类样本所占的比例
理解:
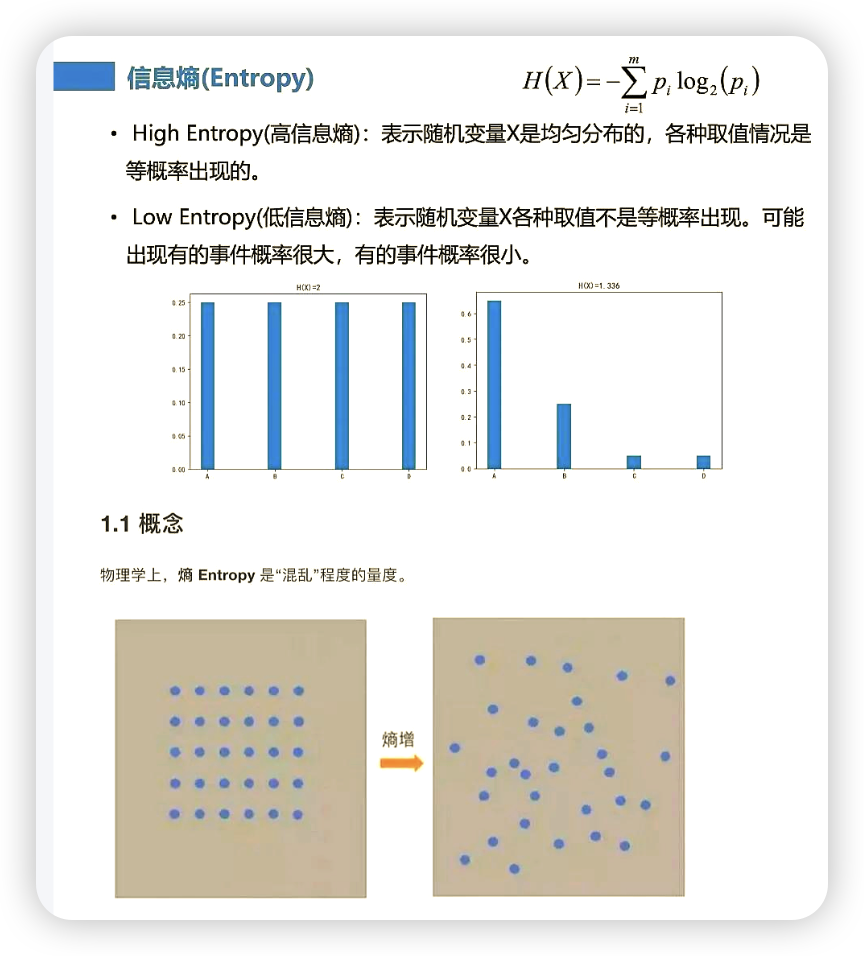
熵越高,数据越混乱,不确定性越大。(例如,一个盒子里有50个红球和50个蓝球,熵最大)
熵越低,数据越纯净,不确定性越小。(例如,一个盒子里有100个红球和0个蓝球,熵为0,最纯净)
2.2.2、信息增益
信息增益= entroy(前)-entroy(后)
注:信息增益表示得知特征X的信息,而使得类Y的信息熵减少的程度
定义:使用某个特征进行分割前后,数据集熵的减少量。信息增益越大,意味着使用这个特征进行分割所带来的“纯度提升”越高。
公式:
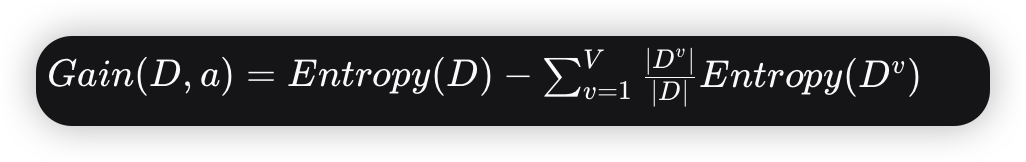
a:某个特征
V:特征 a有多少个不同的取值
Dv:在特征 a 上取值为 v的子数据集
决策树算法(ID3):在每一个节点,选择信息增益最大的那个特征作为分割标准
缺点:对可取值数目较多的特征有偏好(例如“ID”号,每个样本一个值,分割后每个子集熵都为0,信息增益最大,但这毫无意义)
2.2、基尼系数分裂法
定义:另一种衡量数据不纯度的指标。它表示从数据集中随机抽取两个样本,其类别标签不一致的概率
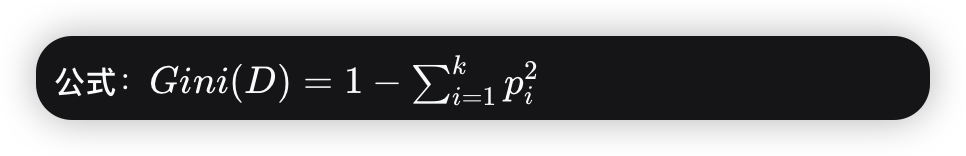
理解:
基尼系数越高,数据越混乱
基尼系数越低,数据越纯净
3、剪枝策略
剪枝策略
决策树容易过拟合,为了防止模型过于复杂而产生的过拟合问题,需要进行剪枝操作:常见的剪枝策略包括预剪枝和后剪枝。预剪枝是在构造决策树时进行剪枝操作,通过设置阈值或限制树的深度等方式来控制决策树的增长。后剪枝是在构造完整的决策树后再进行剪枝操作,通过对叶子节点进行损失函数的优化来减小模型复杂度。
决策树案例和使用技巧
1、代码案例
用到的Python类库:sklearn、matplotlib、JupyterLab
# 导入所需库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score, classification_report
import matplotlib.pyplot as plt
# 1. 加载数据
iris = load_iris()
X = iris.data # 特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度
y = iris.target # 目标变量:鸢尾花类别(0: Setosa, 1: Versicolour, 2: Virginica)
# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 3. 创建决策树分类器,使用基尼不纯度作为划分标准
# 可调整参数:max_depth(树最大深度)、min_samples_split(节点最小分裂样本数)等防止过拟合
clf = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=42)
# 4. 训练模型
clf.fit(X_train, y_train)
# 5. 预测测试集
y_pred = clf.predict(X_test)
# 6. 评估模型
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")
print("\n详细分类报告:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))输出:
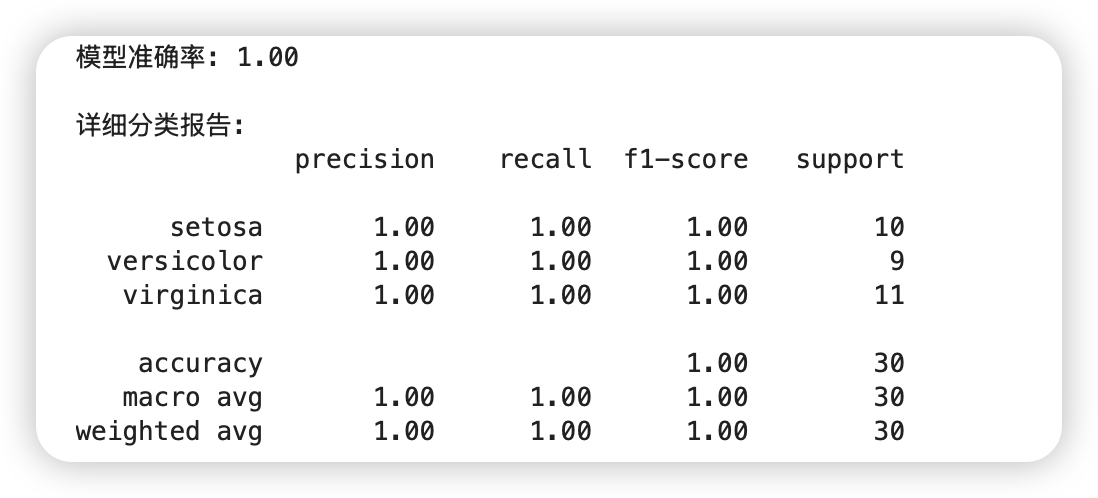
使用刚才的例子绘制决策树:
使用matplotlib的plot_tree可视化决策树
# 设置图形大小
plt.figure(figsize=(12, 8))
# 绘制决策树
plot_tree(clf, filled=True, # 填充颜色表示类别feature_names=iris.feature_names, # 特征名称class_names=iris.target_names, # 类别名称rounded=True, # 圆角边框fontsize=10) # 字体大小
plt.title("决策树 - 鸢尾花分类")
plt.show()输出:
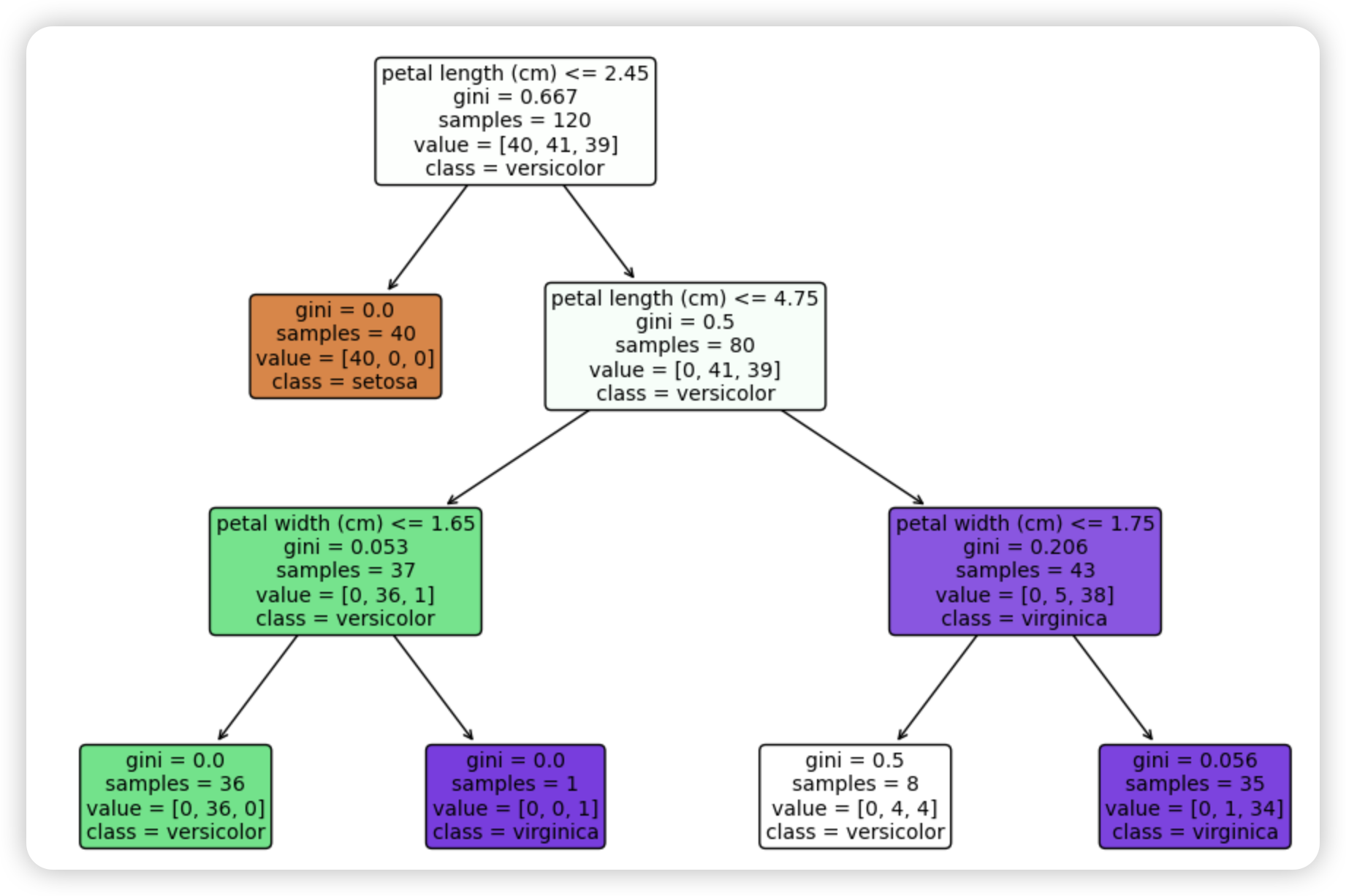
决策树算法参数解释:
在DecisionTreeClassifier中,这些参数能帮助优化模型:
criterion: 分裂标准,可选"gini"(基尼不纯度)或"entropy"(信息增益)
max_depth: 树的最大深度,防止过拟合
min_samples_split: 节点分裂所需的最小样本数
min_samples_leaf: 叶节点所需的最小样本数
random_state: 随机种子,确保结果可重现鸢尾花数据集(Iris Dataset)
1)Iris特征(Features):
花萼长度(sepal length):单位为厘米
花萼宽度(sepal width):单位为厘米
花瓣长度(petal length):单位为厘米
花瓣宽度(petal width):单位为厘米
2)Iris目标变量(Target Variable):
鸢尾花的三个品种(三种类别):
山鸢尾(Iris-Setosa):0
变色鸢尾(Iris-Versicolour):1
维吉尼亚鸢尾(Iris-Virginica):2
3)数据集信息:
样本数:150(每个类别50个样本)
特征数:4(数值型,连续型)
2、决策树使用技巧
数据预处理:决策树对数据量纲不敏感,但缺失值需要处理
特征重要性:训练后可通过
clf.feature_importances_查看特征重要性可视化依赖:需要安装
matplotlib库,如果可视化显示中文乱码,需要额外配置字体
参数调优技巧
| 技巧类别 | 关键点 | 说明/目的 |
|---|---|---|
| 参数调优 | max_depth | 限制树最大深度,防止过拟合 |
min_samples_split | 节点至少样本数,避免过细划分 | |
min_samples_leaf | 叶节点至少样本数,保证划分有效性 | |
criterion | 选择分裂标准,"gini"(基尼系数)或 "entropy"(信息增益)。 | |
| 防止过拟合 | 预剪枝 | 通过上述参数提前停止树生长 |
| 后剪枝 | 生成树后剪枝,ccp_alpha是常用参数 | |
| 集成方法 | 使用随机森林等多棵树降低过拟合风险 | |
| 数据预处理 | 处理数值特征 | 决策树本身不要求标准化,但可能受益于区间离散化 |
| 处理类别特征 | 需要使用OrdinalEncoder或OneHotEncoder进行编码 | |
| 处理缺失值 | 决策树对缺失值相对不敏感,但需处理,例如使用特定值填充 | |
| 模型理解与调优 | 可视化决策树 | 利用plot_tree或export_graphviz绘制树形图,直观理解决策过程 |
| 分析特征重要性 | 通过model.feature_importances_查看特征重要性,辅助特征选择 |
