用Python来学微积分25-微积分中的函数奥秘:单调性、极值与最值
文章目录
- 一、函数的单调性
- 1. 概念讲解
- 2. 手动求解步骤
- 3. Python 案例
- 二、函数的极值
- 1. 概念讲解
- 2. 手动求解步骤
- 3. Python 案例
- 三、函数的最值
- 1. 概念讲解
- 2. 手动求解步骤
- 3. Python 案例
宝子们,今天咱们一起深入微积分的奇妙世界,探索函数的单调性、极值和最值这些重要概念!别担心,我会结合超有趣的 Python 案例,让这些知识变得通俗易懂~
一、函数的单调性
1. 概念讲解
函数的单调性描述的是函数值随着自变量的增大或减小而变化的趋势。如果函数在某个区间上,自变量增大时函数值也增大,那就是单调递增;反之,自变量增大时函数值减小,就是单调递减。
2. 手动求解步骤
对于一个函数 y=f(x)y = f(x)y=f(x),我们可以通过求它的导数 f′(x)f'(x)f′(x) 来判断单调性:
- 求出函数的导数 f′(x)f'(x)f′(x)。
- 令 f′(x)>0f'(x) > 0f′(x)>0,解出不等式的区间,这些区间就是函数的单调递增区间。
- 令 f′(x)<0f'(x) < 0f′(x)<0,解出不等式的区间,这些区间就是函数的单调递减区间。
3. Python 案例
我们以函数 y=x2−3xy = x^2 - 3xy=x2−3x 为例,来看看它的单调性。首先,我们需要导入 Python 的科学计算库 numpy 和绘图库 matplotlib。
import numpy as np
import matplotlib.pyplot as plt# 定义函数
def f(x):return x**2 - 3*x# 求导
def df(x):return 2*x - 3# 生成 x 值
x = np.linspace(-2, 4, 100)
y = f(x)
dy = df(x)# 绘制函数图像和导数图像
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(x, y, label='y = x^2 - 3x')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()plt.subplot(2, 1, 2)
plt.plot(x, dy, label="y' = 2x - 3", color='r')
plt.xlabel('x')
plt.ylabel("y'")
plt.axhline(y=0, color='k', linestyle='--')
plt.legend()plt.tight_layout()
plt.show()# 判断单调性
critical_point = 3 / 2
print(f"当 x < {critical_point} 时,导数小于 0,函数单调递减。")
print(f"当 x > {critical_point} 时,导数大于 0,函数单调递增。")
运行结果:
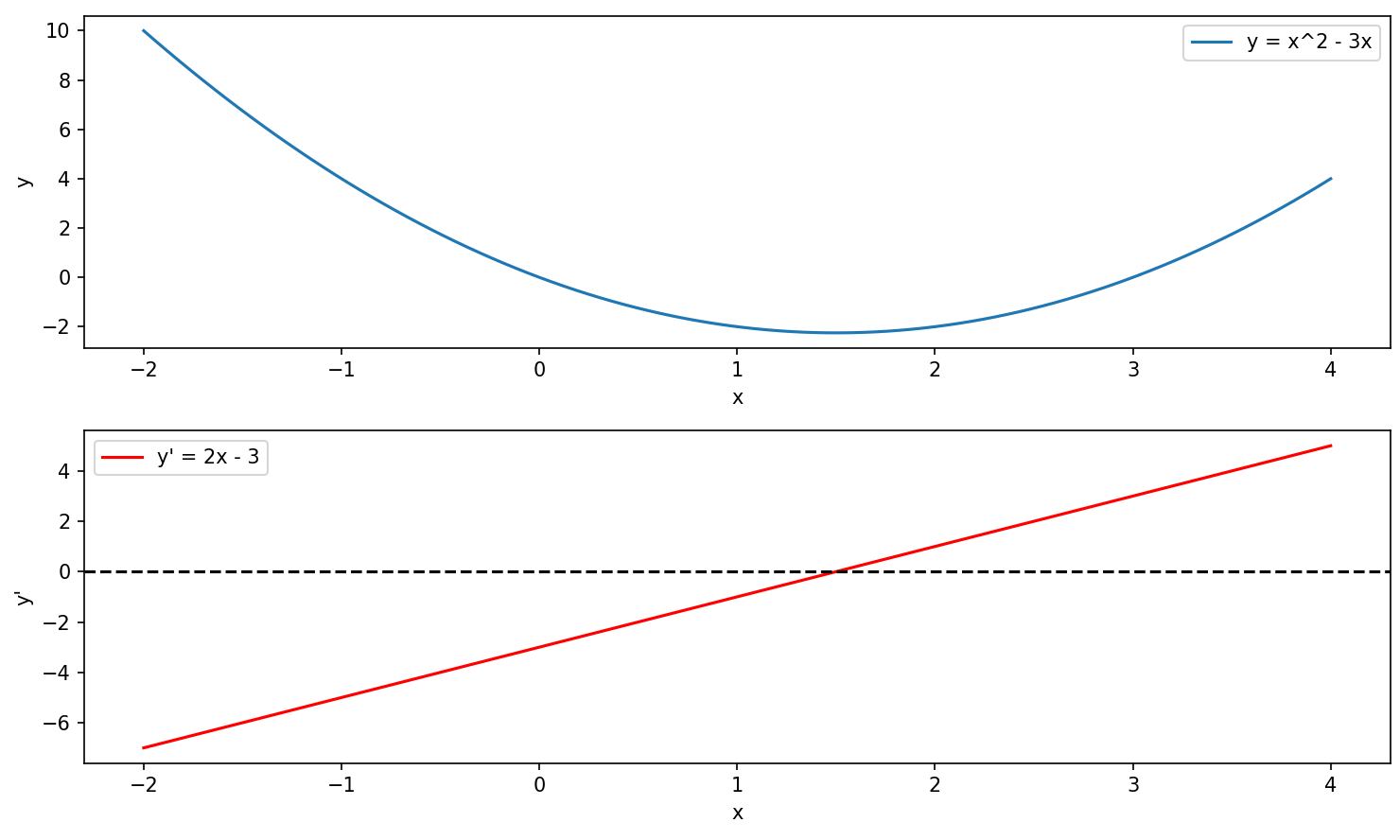

在这个案例中,我们先定义了原函数和它的导数函数,然后通过 numpy 生成一系列 xxx 值并计算对应的函数值和导数值,最后绘制出函数图像和导数图像。从导数的正负我们可以清楚地看到函数的单调性变化。
二、函数的极值
1. 概念讲解
极值是函数在某个局部范围内的最大值或最小值。也就是说,在极值点附近,函数值比周围的点都大(极大值)或者都小(极小值)。
2. 手动求解步骤
求函数 f(x)f(x)f(x) 极值的一般步骤如下:
- 确定函数的定义域。
- 求导数 f′(x)f'(x)f′(x)。
- 令 f′(x)=0f'(x) = 0f′(x)=0,求出驻点,以及找出 f′(x)f'(x)f′(x) 不存在的点。
- 列表分析这些点两侧导数的正负性,确定是极大值点还是极小值点。
- 将极值点代入原函数,求出对应的极值。
3. Python 案例
同样以函数 y=x2−3xy = x^2 - 3xy=x2−3x 为例,用 Python 来找到它的极值。
from scipy.optimize import minimize_scalar# 定义函数
def f(x):return x**2 - 3*x# 寻找极小值
res = minimize_scalar(f)
min_x = res.x
min_y = f(min_x)print(f"函数的极小值点为 x = {min_x},极小值为 y = {min_y}")
这里我们使用了 scipy 库中的 minimize_scalar 函数来寻找函数的极小值。当然,我们也可以手动按照上述步骤,先求导找到驻点,再判断是极大值还是极小值。

三、函数的最值
1. 概念讲解
最值是函数在整个定义域内的最大值和最小值。它可能是区间端点处的函数值,也可能是区间内的极值。
2. 手动求解步骤
求连续函数 f(x)f(x)f(x) 在闭区间 [a,b][a, b][a,b] 上的最值步骤如下:
- 求出函数在 (a,b)(a, b)(a,b) 内所有的驻点和导数不存在的点。
- 计算函数在这些点以及区间端点 aaa 和 bbb 处的函数值。
- 比较这些函数值的大小,最大的就是最大值,最小的就是最小值。
3. Python 案例
假设我们有一个函数 y=3x23−2xy = 3\sqrt[3]{x^2} - 2xy=33x2−2x,在区间 [−1,12][-1, \frac{1}{2}][−1,21] 上求它的最值。
import numpy as np# 定义函数
def f(x):return 3 * np.cbrt(x**2) - 2*x# 区间端点
a = -1
b = 0.5# 生成区间内的点
x_values = np.linspace(a, b, 100)
y_values = f(x_values)# 绘制函数图像
import matplotlib.pyplot as plt
plt.plot(x_values, y_values)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Function y = 3√[3]{x^2} - 2x on [-1, 0.5]')
plt.show()# 寻找临界点:包括导数为零的点(驻点)和导数不存在的点
# 由于导数 f'(x) = 2*x^(-1/3) - 2,令导数为零得 x=1(不在区间内),导数不存在的点为 x=0
critical_points = [a, b, 0] # 包括端点和 x=0y_endpoints = [f(x) for x in critical_points]max_index = np.argmax(y_endpoints)
min_index = np.argmin(y_endpoints)print(f"函数在区间 [{a}, {b}] 上的最大值为 {y_endpoints[max_index]},在 x = {critical_points[max_index]} 处取得。")
print(f"函数在区间 [{a}, {b}] 上的最小值为 {y_endpoints[min_index]},在 x = {critical_points[min_index]} 处取得。")
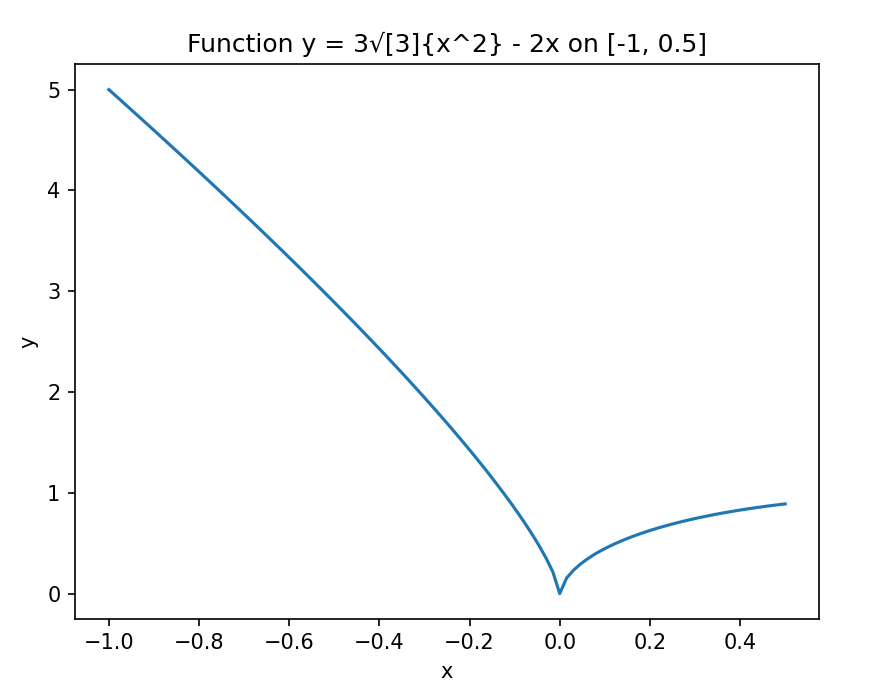

通过这个案例,我们不仅用 Python 绘制了函数图像直观地观察最值情况,还简单演示了求解最值的流程。
宝子们,今天的微积分知识分享就到这里啦!希望这些内容能让你对函数的单调性、极值和最值有更清晰的理解。如果你觉得有用,别忘了点赞、关注哦!也欢迎在评论区留言,说说你对这些知识的理解或者提出疑问,咱们一起交流进步~
往期精彩回顾:
- 用Python来学微积分23-微分中值定理
- 用Python来学微积分24-洛必达法则
专栏导航目录 《程序员AI之路:从Python起步》完全学习导航
完整代码已开源 ai-learning-path,欢迎Star和Fork!
下期预告:在下一篇文章中,我们将开始学习洛必达法则。
参考资料:
- 扈志明《微积分》教材
互动邀请:如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!
