当前位置：首页 > news >正文

图的邻接表实现及遍历

news 2025/11/2 6:50:37

图的邻接表实现及遍历

文章目录

图的邻接表实现及遍历
- 一、前言
- 二、邻接表的实现
- - 2.1 定义结构
  - 2.2 创建邻接表
  - 2.3 释放邻接表
  - 2.4 初始化
  - 2.5 添加边
  - 2.6 访问
  - 2.7 深度遍历
  - 2.7 广度遍历
- 三、应用
- - 3.1 优点
  - 3.2 缺点
  - 3.3 应用
- 四、小结

一、前言

先前我们已经学过了图的几种存储方式，今天就图的邻接表来探讨一下它的实现~

二、邻接表的实现

邻接表分为正邻接表和负邻接表。今天将以正邻接表为例进行解读~

2.1 定义结构

定义顶点结构，边结构，图结构。

// 边的结构
typedef struct arcEdge
{int no;					// 边的顶点编号int weight;				// 边的权值（后期会有用，在这里取1用作占位）struct arcEdge *next;	// 指向下一条边结构
} ArcEdge;// 顶点结构
typedef struct
{int no;					// 顶点编号，方便查找char *show;				// 顶点的显示内容ArcEdge *firstEdge;		// 当前节点指向其他节点形成的边的链表首地址
} ArcNode;// 邻接表来表示图，多个顶点的结构来描述
typedef struct
{ArcNode *nodes;			// 图中顶点的集合int nodeNum;			// 图中顶点的个数int edgeNum;			// 图中边的个数int directed;			// 是否是有向图int *visited;			// 图遍历时的已遍历标志
} AGraph;

2.2 创建邻接表

easy~

// 产生n个节点的邻接表
AGraph *createAGraph(int n)
{AGraph *graph = malloc(sizeof(AGraph));if(graph == NULL){return NULL;}graph->nodeNum = n;graph->edgeNum = 0;graph->directed = 0;graph->nodes = malloc(sizeof(ArcNode) * n);graph->visited = malloc(sizeof(int) * n);if(graph->nodes == NULL || graph->visited == NULL){free(graph);return NULL;}memset(graph->nodes, 0, sizeof(ArcNode) * n);memset(graph->visited, 0, sizeof(int) * n);return graph;
}

2.3 释放邻接表

easy~

void releaseAGraph(AGraph *graph)
{if (graph){if (graph->nodes){free(graph->nodes);}if (graph->visited){free(graph->visited);}free(graph);}
}

2.4 初始化

easy~

如图：

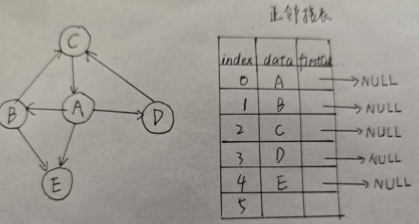
在这里插入图片描述

void initAGraph(AGraph* graph, char *names[], int num, int directed)
{graph->directed = directed;for(int i = 0; i < num; ++i){graph->nodes[i].no = i;graph->nodes[i].show = names[i];graph->nodes[i].firstEdge = NULL;}
}

2.5 添加边

判断顶点的合法性
创建边
处理新的边，建立关系

如图：

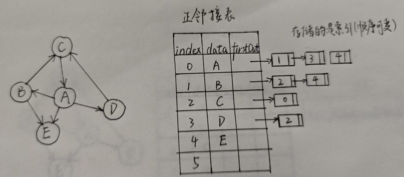
在这里插入图片描述

// parameter:
// graph: 向哪个图添加边
// x	：起始顶点的编号
// y	：终点的顶点编号
// w	：边的权值
// 创建边
static ArcEdge *createArcEdge(int v, int w)
{ArcEdge *edge = malloc(sizeof(ArcEdge));if(edge == NULL){return NULL;}edge->no = v;edge->weight = w; edge->next = NULL;
}
// 添加边
void addAGraph(AGraph *graph, int x, int y, innt weight)
{// 判断边的合法性if(x < 0 || x >= graph->nodeNum || y < 0 || y > = graph->nodeNum){return;}if(x == y)			// 这里是简单图，因此没有自己指向自己的边{return;}// 产生了新节点ArcEdge *edge = createArcEdge(y, w);// 先处理新节点——头插法edge->next = graph->nodes[x].firstEdge;node[x].firstEdge = edge;graph->edgeNum++;if(graph->directed == 0){// 反方向建立边edge = createArcEdge(x, w);edge->next = graph->nodes[y].firstEdge;graph->node[y].firstEdge = edge;graph->edgeNum++;}
}

2.6 访问

easy~

void visitAGraphNode(const ArcNode *node)
{printf("\t%s", node->show);
}

2.7 深度遍历

从一个顶点出发，访问
继续遍历邻接点，随着p指针不断移动，实现深入遍历（一条道走到黑）

// parameter:v：从哪个点开始的
void DFS_AGraph(const AGraph *graph, int v)
{ArcEdge *p;         // 辅助指针// 访问vgraph->visited[v] = 1;visitAGraphNode(&graph->nodes[v]);// 开始“拆”p = graph->nodes[v].firstEdge;while (p){// 判断是否访问过if (graph->visited[p->no] == 0){DFS_AGraph(graph, p->no);}// 实现深入遍历邻接点的重要步骤p = p->next;}
}

2.7 广度遍历

入队第一个，标记
出队访问，入队其对应的链表
继续出队访问
循环上述过程

void BFS_AGraph(const AGraph *graph, int v)
{// 申请一个临时队列int *que = malloc(sizeof(int) * graph->nodeNum);int front = 0, rear = 0;// 辅助指针，方便处理ArcEdge *p;int cur;// 入队rear = (rear + 1) % graph->nodeNum;que[rear] = v;graph->visited[v] = 1;while (front != rear){// 先加再取front = (front + 1) % graph->nodeNum;// 访问cur = que[front];visitAGraphNode(&graph->nodes[cur]);// 入队p = graph->nodes[cur].firstEdge;while (p){if (graph->visited[p->no] == 0)     // 判断是否访问{rear = (rear + 1) % graph->nodeNum;que[rear] = p->no;graph->visited[p->no] = 1;}p = p->next;}}// 释放free(que);
}