深度学习（9）导数与计算图
一、导数（Derivative）
1. 导数的定义与直观理解
导数（Derivative）描述的是一个函数在某一点处的“变化率”。换句话说，它告诉我们：
当输入（x）发生一个非常小的变化时，输出（y）会随之变化多少。
数学定义为：
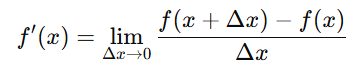
例如：
这表示：在点 x=3x=3x=3 时，斜率是 6，即输入每增加 1，输出大约增加 6。
2. 导数的几何意义
在图像上，导数代表函数曲线在某一点的切线斜率（slope of tangent line）。
当导数为正，函数上升；
当导数为负，函数下降；
当导数为 0，函数在该点处平缓（可能是极值点）。
3. 导数在代码中的使用
在深度学习框架（如 TensorFlow 或 PyTorch）中，导数的计算被封装成“自动微分”（Automatic Differentiation）功能。
例如在 PyTorch 中：
import torch# 定义变量
x = torch.tensor(3.0, requires_grad=True)
y = x ** 2 + 2 * x + 1# 自动求导
y.backward()
print(x.grad) # 输出导数 dy/dx = 2x + 2 = 8
这段代码展示了如何让计算机“自动”计算导数，背后其实就是在构建计算图（Computation Graph），并通过反向传播进行梯度计算。
二、计算图（Computation Graph）
1. 基本概念
计算图是神经网络中表示计算流程的一种图结构。它将复杂的函数分解为一系列简单的节点操作（如加法、乘法、激活函数等）。
例如：
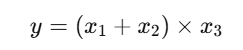
对应的计算图为：
x1 ─┐├─( + )──┐ x2 ─┘ │├─( × )──► y x3 ───────────┘
2. 从右向左的反向传播原理
在反向传播中，计算导数时要遵循链式法则（Chain Rule）：
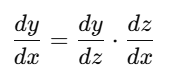
计算图会从输出节点（右边）开始，逐步往输入节点（左边）反传梯度，这就是“从右向左计算”的原因。
为什么这样做？因为输出的误差（Loss）依赖于所有中间节点的结果，而每个中间节点的导数又取决于其“下游节点”的梯度。反向传播就是利用这种依赖关系，逐层传递误差信息。
3. 计算图中梯度的依赖关系
在计算图中，我们常用 cadj 表示某节点的“梯度累积值”（gradient accumulation）。每个节点的梯度由下游节点传回并逐步累加：
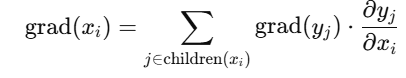
也就是说，一个节点的梯度取决于它所影响的所有下游节点的梯度。
4. 为什么只需要计算 n + p 次导数？
假设：
计算图中有 n 个中间节点
有 p 个参数（parameters）
那么在一次反向传播中，我们可以同时得到所有参数的梯度。这得益于计算图的结构：每个节点的导数只需要计算一次，然后梯度信息被“复用”并向上游传播。所以，总共只需要 n+p 次计算，而不是 n×p 次。这正是反向传播（Backpropagation）高效的关键。
5. 计算图在神经网络中的应用
在神经网络中，整个模型的计算过程都可以看作一个巨大的计算图：
每一层的输出
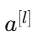都是由上一层的输出 
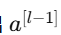经过线性变换 + 激活函数得到；计算图会自动记录这些运算关系；
在反向传播时，框架根据计算图自动计算每个参数（权重、偏置）的梯度。
例如 PyTorch 的示意：
import torch
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x * 2
z = y.mean()
z.backward()
print(x.grad) # 输出 [0.6667, 0.6667, 0.6667]
这里 PyTorch 自动构建了如下计算图：
x → (×2) → y → (mean) → z
并自动执行了反向传播计算。
总结
| 概念 | 作用 |
|---|---|
| 导数（Derivative） | 衡量输出对输入的敏感程度（变化率） |
| 计算图（Computation Graph） | 表示函数的计算流程结构 |
| 反向传播（Backpropagation） | 从输出误差反向计算梯度 |
| 自动微分（Autograd） | 框架自动计算梯度的功能 |
| n + p 原理 | 每个节点和参数的梯度只需计算一次，提高效率 |