二分查找为什么总是写错

目录

1讲解:一篇讲懂二分查找

2总结

主要是倒数第二张图,搞懂就可以不用看下面了

---

1讲解:一篇讲懂二分查找

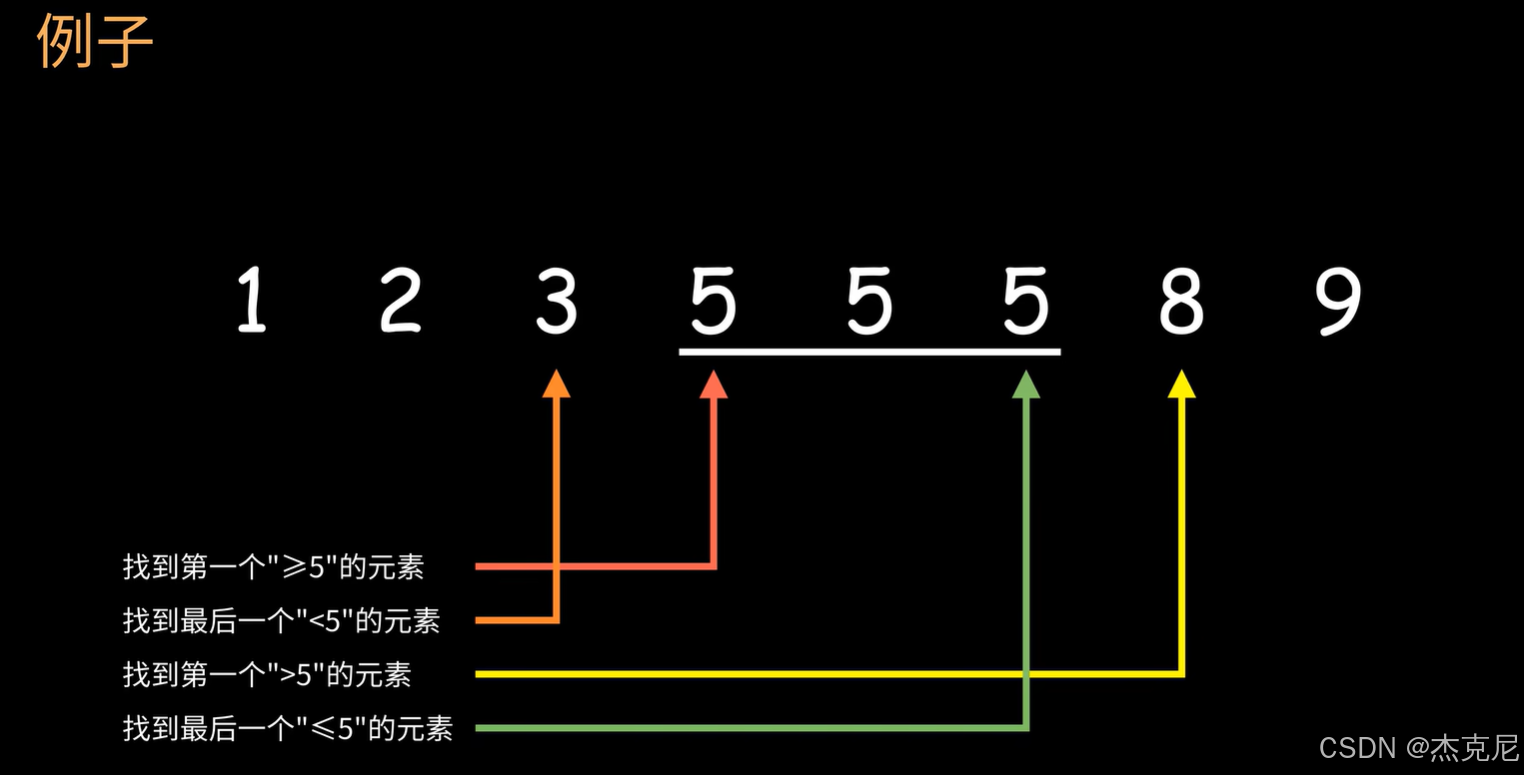
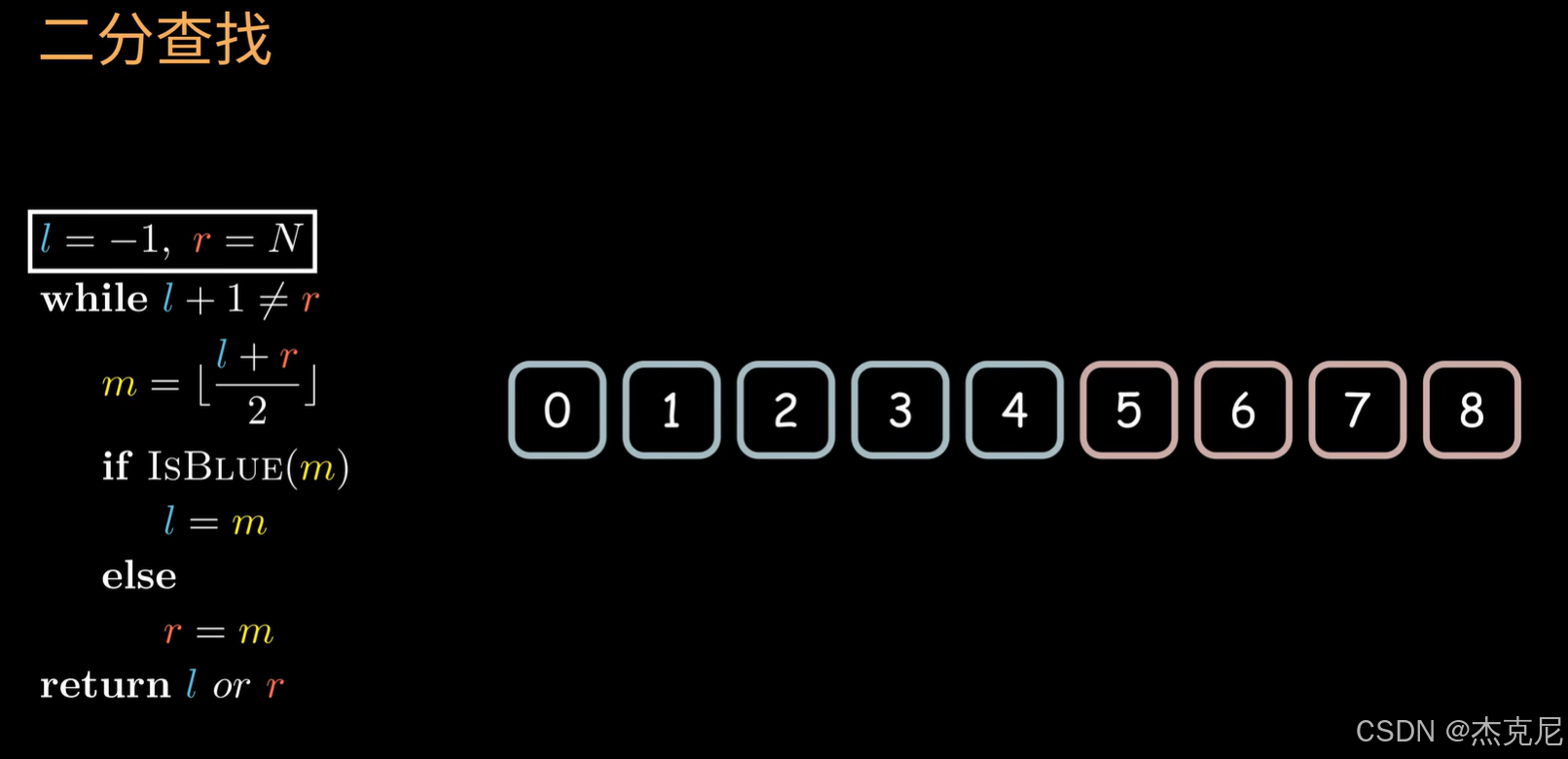
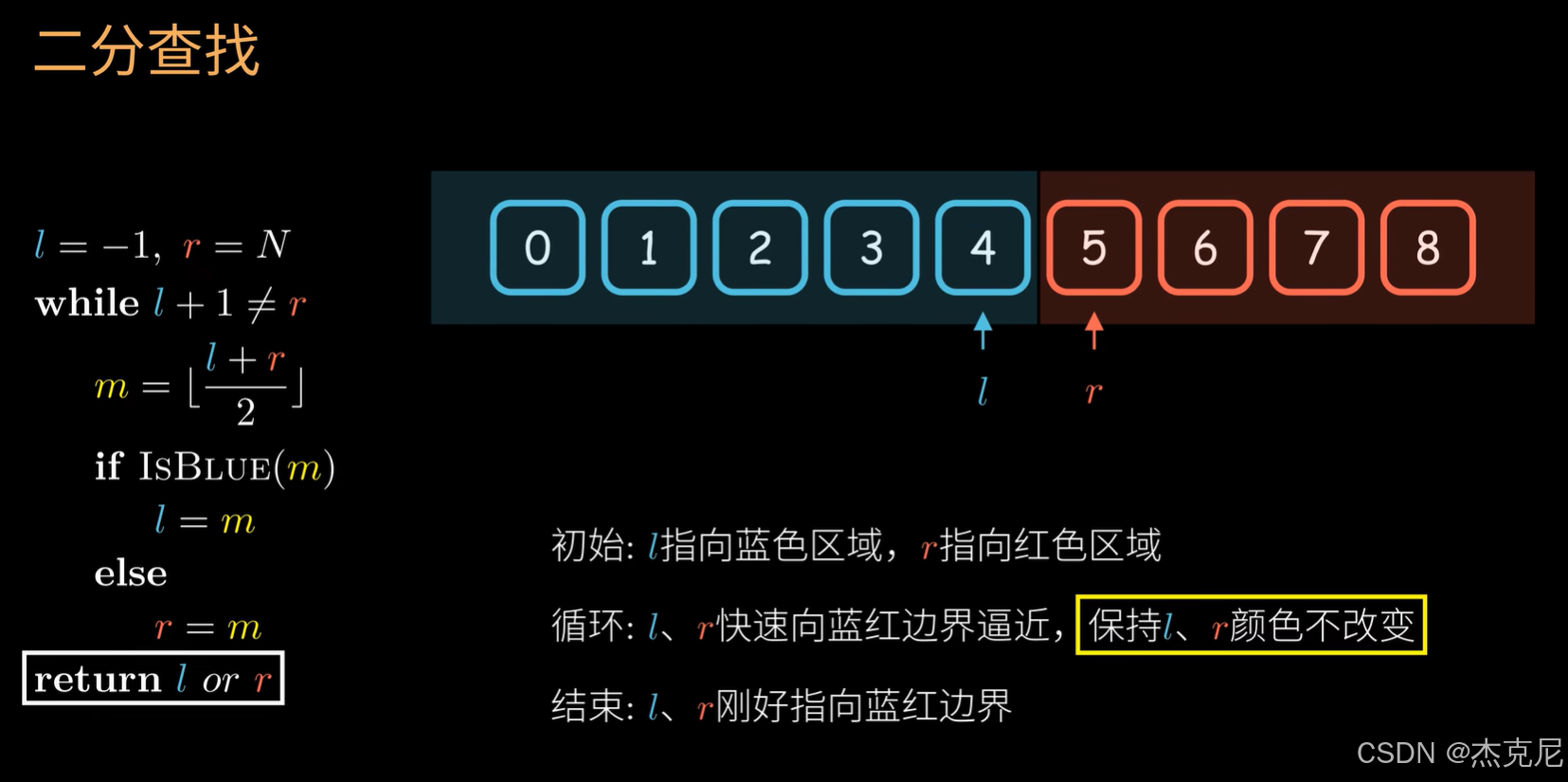
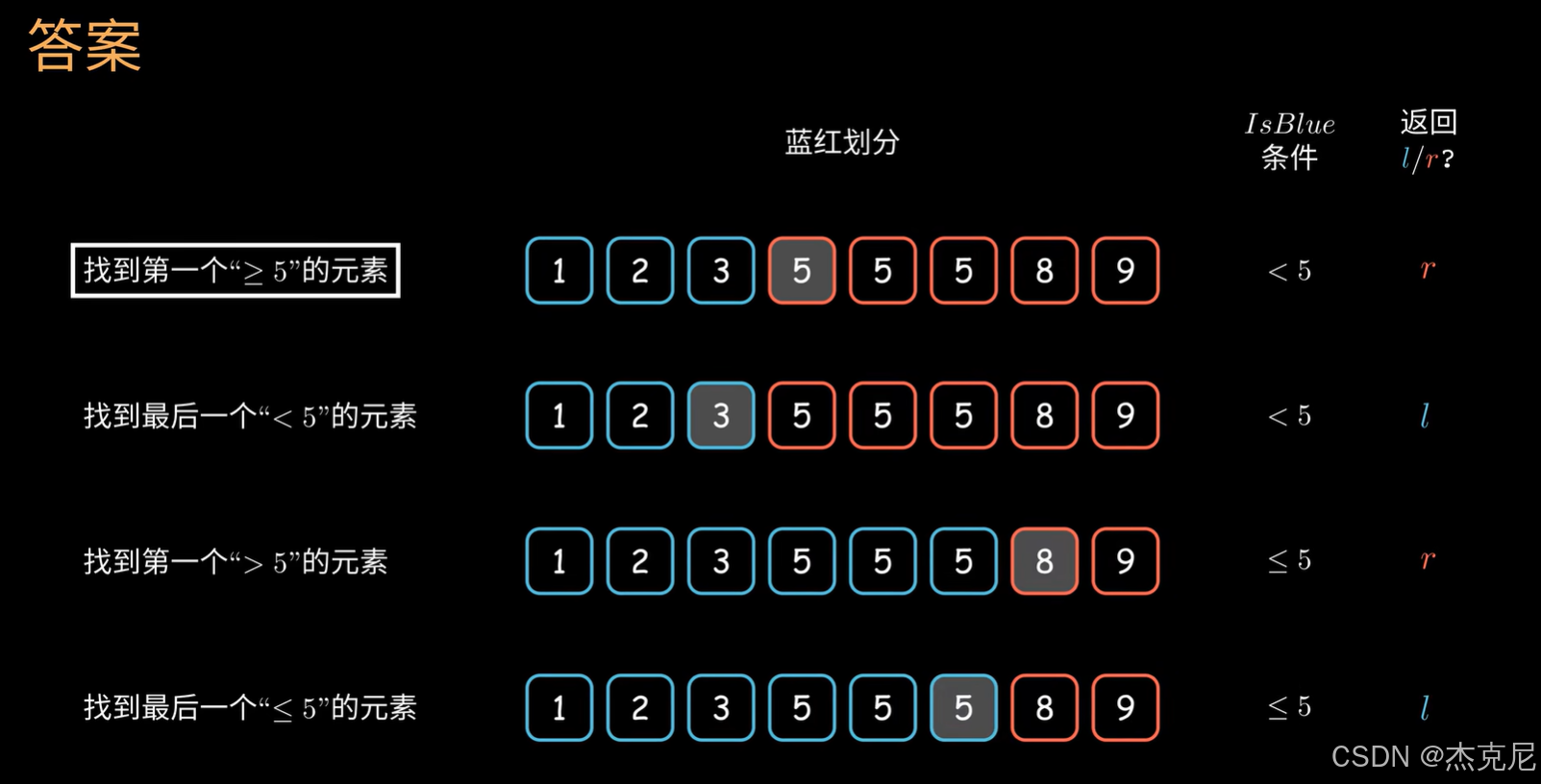
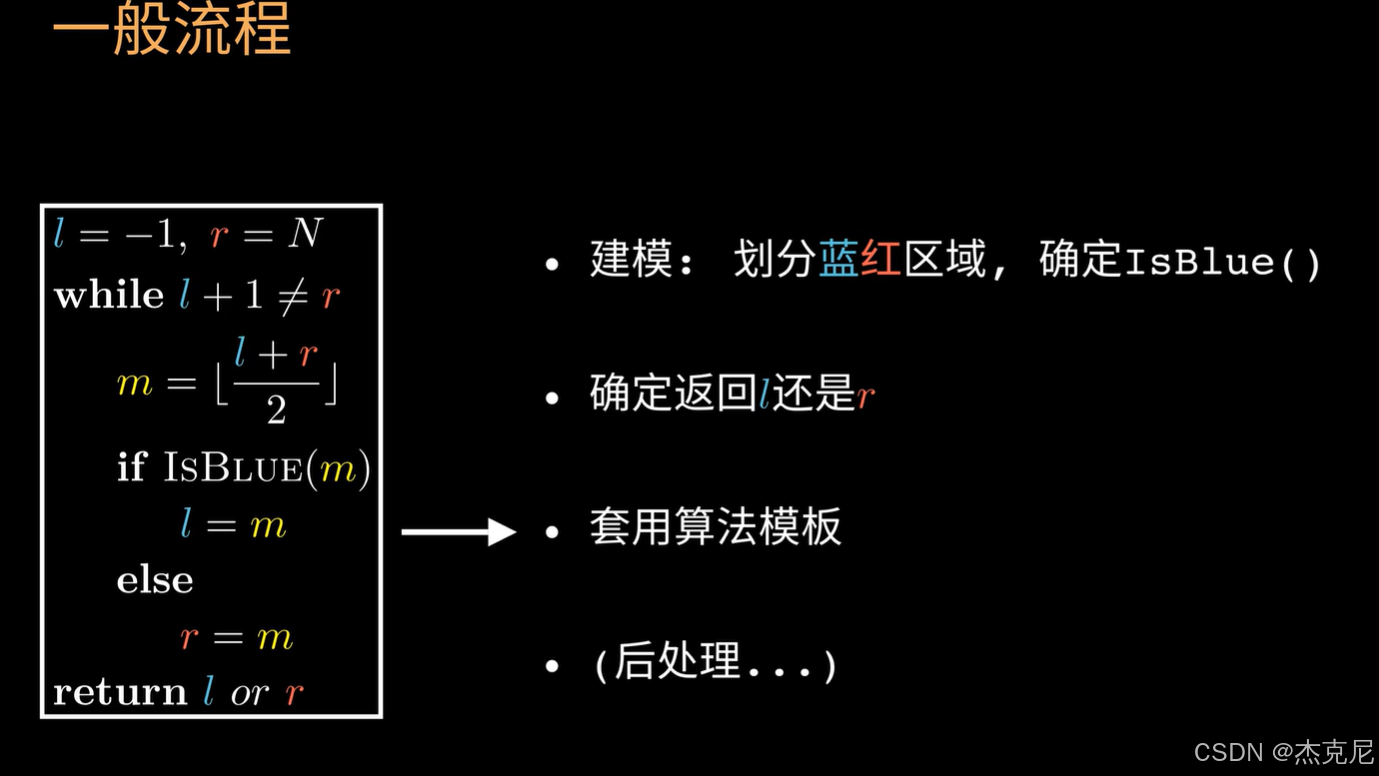
2总结

主要是倒数第二张图,搞懂就可以不用看下面了

二分查找的开区间写法：从原理到实战的优雅实现
二分查找（Binary Search）是计算机科学中最经典的算法之一，其时间复杂度为 O (log n)，在有序数据集中的查找效率远超线性查找。但二分查找的实现细节往往令人头疼 —— 边界条件的处理（如 while 循环的终止条件、mid 的计算方式、左右指针的移动规则）稍有不慎就会出现死循环或漏查。
本文将聚焦开区间形式的二分查找实现，从原理剖析到代码落地，再到实战应用，带你理解这种写法的优雅之处：无需纠结边界是否包含，逻辑更清晰，容错率更高。
一、什么是 “开区间”？理解二分查找的区间定义
在二分查找中，“区间” 指的是当前查找的有效范围，通常由左指针 left 和右指针 right 界定。不同的区间定义会导致完全不同的实现逻辑，而开区间是其中最具代表性的一种。
1. 区间的三种常见定义
二分查找的区间定义本质上是对 left 和 right 所指向范围的 “语义约定”，常见的有三种：
闭区间 [left, right]：当前查找范围包含 left 和 right 指向的元素（即 left <= right 时区间有效）。
左闭右开 [left, right)：包含 left 指向的元素，不包含 right 指向的元素（left < right 时区间有效）。
开区间 (left, right)：既不包含 left，也不包含 right（left + 1 < right 时区间有效，较少见）。
本文重点讲解左闭右开 [left, right)（简称 “开区间形式”，实际是半开半闭，是工程中最常用的开区间写法），因为它完美平衡了逻辑简洁性和实用性。
2. 开区间 [left, right) 的核心约定
采用左闭右开区间时，我们对 left 和 right 有明确的语义规定：
left：当前查找范围的第一个有效元素（包含在区间内）。
right：当前查找范围的第一个无效元素（不包含在区间内），即区间的边界在有效元素之后。
区间有效条件：left < right（当 left == right 时，区间内无元素，查找结束）。
举个例子：在数组 [1, 3, 5, 7, 9] 中查找元素，初始开区间为 [0, 5)（数组下标从 0 开始，right=5 对应数组长度，恰好是最后一个元素下标 4 的下一位，不包含在区间内）。
二、开区间二分查找的原理：为什么它更优雅？
开区间写法的优雅之处在于 **“边界语义一致”**：始终遵循 “左含右不含” 的规则，避免了闭区间中 “是否包含边界” 的纠结。我们通过 “查找目标值的位置” 案例，逐步拆解其原理。
1. 步骤拆解：以查找目标值 target 为例
假设在有序数组 nums 中查找 target，返回其下标（若不存在则返回 -1），开区间写法的步骤如下：
（1）初始化区间
左指针 left = 0（指向数组第一个元素，包含在区间内）。
右指针 right = nums.length（指向数组长度，不包含在区间内，因数组最大下标为 nums.length - 1）。
初始区间：[0, nums.length)，覆盖整个数组。
（2）循环查找（while (left < right)）
当 left < right 时，区间内仍有元素，继续查找：
计算中间位置 mid = left + (right - left) / 2（等价于 (left + right) / 2，但避免整数溢出）。
比较 nums[mid] 与 target：
若 nums[mid] == target：找到目标，返回 mid。
若 nums[mid] > target：目标在左半区间，调整右指针 right = mid（因右区间不含 mid，新区间为 [left, mid)）。
若 nums[mid] < target：目标在右半区间，调整左指针 left = mid + 1（因左区间含 left，新区间为 [mid + 1, right)）。
（3）循环结束
当 left == right 时，区间 [left, right) 为空，说明未找到目标，返回 -1。
2. 案例演示：在 [1, 3, 5, 7, 9] 中查找 5
初始：left=0，right=5，区间 [0,5)（元素 [1,3,5,7,9]）。
第一次循环：mid = 0 + (5-0)/2 = 2，nums[2] = 5，等于 target，返回 2（查找成功）。
另一个案例：查找 4（不存在）：
初始：left=0，right=5，mid=2，nums[2]=5 > 4 → right=2，区间变为 [0,2)（元素 [1,3]）。
第二次循环：left=0 < right=2，mid=0 + (2-0)/2=1，nums[1]=3 < 4 → left=2，区间变为 [2,2)（空）。
循环结束，返回 -1（查找失败）。
3. 开区间写法的核心优势
对比闭区间 [left, right] 的写法，开区间 [left, right) 有三个显著优势：
边界处理更简单：无需考虑 left <= right 还是 left < right，循环条件固定为 left < right。
指针移动更统一：调整 right 时直接赋值 mid（因右不包含），调整 left 时赋值 mid + 1（因左包含），规则清晰。
初始 right 更直观：right 初始值为数组长度，无需记忆 nums.length - 1，符合 “开区间不包含边界” 的直觉。
三、代码实现：开区间二分查找的基础版与进阶版
掌握原理后，我们来落地代码。从基础的 “查找目标值” 到进阶的 “查找边界”，开区间写法的逻辑一致性会体现得淋漓尽致。
1. 基础版：查找目标值的位置
java
运行
public int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 开区间右边界：不包含最后一个元素的下一位
    
    while (left < right) { // 区间有效条件：left < right
        int mid = left + (right - left) / 2; // 避免 (left + right) 溢出
        if (nums[mid] == target) {
            return mid; // 找到目标，返回下标
        } else if (nums[mid] > target) {
            right = mid; // 目标在左半区间，右边界移至 mid（不包含 mid）
        } else {
            left = mid + 1; // 目标在右半区间，左边界移至 mid + 1（包含新 left）
        }
    }
    return -1; // 区间为空，未找到
}
2. 进阶版 1：查找目标值的左边界（第一个出现的位置）
当数组中存在重复元素时，需查找目标值第一次出现的位置（如 [1,2,2,3] 中查找 2 的左边界为 1）。开区间写法的逻辑如下：
java
运行
public int findLeftBound(int[] nums, int target) {
    int left = 0;
    int right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 找到目标后不返回，继续收缩右边界以查找更左的位置
            right = mid; 
        } else if (nums[mid] > target) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    // 循环结束时 left == right，检查是否为目标值
    if (left == nums.length) return -1; // 超出数组范围
    return nums[left] == target ? left : -1;
}
逻辑解析：当 nums[mid] == target 时，不立即返回，而是通过 right = mid 收缩右边界，继续在左半区间 [left, mid) 中查找，直到区间为空（left == right），此时 left 即为左边界（若存在）。
3. 进阶版 2：查找目标值的右边界（最后一个出现的位置）
查找目标值最后一次出现的位置（如 [1,2,2,3] 中查找 2 的右边界为 2）：
java
运行
public int findRightBound(int[] nums, int target) {
    int left = 0;
    int right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 找到目标后不返回，继续收缩左边界以查找更右的位置
            left = mid + 1; 
        } else if (nums[mid] > target) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    // 循环结束时 left == right，右边界为 left - 1
    if (left == 0) return -1; // 超出数组范围
    return nums[left - 1] == target ? left - 1 : -1;
}
逻辑解析：当 nums[mid] == target 时，通过 left = mid + 1 收缩左边界，继续在右半区间 [mid + 1, right) 中查找，直到区间为空。此时 left - 1 即为右边界（若存在），因为最后一次找到目标时 left 已被移至 mid + 1。
四、避坑指南：开区间写法的常见错误与解决
即使是开区间写法，也可能因细节疏忽导致错误。以下是三个高频错误及解决方案：
1. 错误：mid 计算导致的整数溢出
问题：若直接用 (left + right) / 2 计算 mid，当 left 和 right 都是大整数时（如 left = 2^30，right = 2^30 + 1），left + right 可能超出 int 类型的最大值，导致溢出。解决：用 left + (right - left) / 2 替代，两者数学结果一致，但避免了溢出。
2. 错误：查找边界时未判断数组范围
问题：在查找左 / 右边界时，循环结束后直接返回 left 或 left - 1，未检查是否超出数组下标（如数组为空时 left = 0，返回 left - 1 会导致 -1，但需确认是否为有效目标）。解决：先判断 left 是否超出数组范围（如左边界检查 left == nums.length，右边界检查 left == 0），再验证目标值是否存在。
3. 错误：混淆 “开区间” 与 “闭区间” 的指针移动规则
问题：习惯了闭区间写法的开发者，可能在开区间中错误地将 right 设为 mid - 1（导致漏查），或 left 设为 mid（导致死循环）。解决：牢记开区间的核心规则 —— 左含右不含：
nums[mid] > target → right = mid（右不包含，直接缩到 mid）；
nums[mid] < target → left = mid + 1（左包含，跳过 mid 缩到 mid + 1）。
五、实战应用：开区间二分查找的典型场景
二分查找的应用远不止 “查找目标值”，开区间写法在以下场景中能发挥巨大作用：
1. 有序数组中的插入位置（LeetCode 35）
问题：给定有序数组和目标值，若目标存在则返回下标，否则返回插入位置（保证数组有序）。开区间解法：本质是查找目标值的左边界，若不存在则 left 即为插入位置。
java
运行
public int searchInsert(int[] nums, int target) {
    int left = 0;
    int right = nums.length;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] >= target) { // 寻找第一个 >= target 的位置
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left; // 无论是否找到，left 都是插入位置
}
2. 求平方根（LeetCode 69）
问题：计算非负整数 x 的平方根，返回整数部分（如 x=8 时返回 2）。开区间解法：在 [0, x+1) 区间内查找最大的 mid，使得 mid * mid <= x。
java
运行
public int mySqrt(int x) {
    if (x == 0) return 0;
    int left = 1;
    int right = x + 1; // 开区间右边界，避免 x=1 时的边界问题
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (mid > x / mid) { // 等价于 mid*mid > x，避免溢出
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left - 1; // 最后一次满足条件的 mid 是 left - 1
}
3. 旋转数组的最小数字（LeetCode 153）
问题：在旋转有序数组（如 [3,4,5,1,2]）中查找最小元素。开区间解法：通过比较 mid 与 right-1（右边界的前一个元素），判断最小值在左半还是右半区间。
java
运行
public int findMin(int[] nums) {
    int left = 0;
    int right = nums.length;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < nums[right - 1]) { // 右半区间有序，最小值在左半
            right = mid + 1;
        } else { // 左半区间有序，最小值在右半
            left = mid + 1;
        }
    }
    return nums[left - 1];
}
六、总结：为什么推荐开区间写法？
二分查找的核心难点在于边界条件的一致性—— 一旦区间定义的语义混乱，就会出现各种 Bug。而开区间 [left, right) 写法通过 “左含右不含” 的严格约定，将复杂的边界判断简化为统一的规则：
初始区间：left=0，right=nums.length（直观且无需减 1）。
循环条件：left < right（区间非空的唯一判断）。
指针移动：right=mid 或 left=mid+1（完全遵循 “左含右不含”）。
这种一致性让开发者无需在每次实现时重新思考边界细节，大幅降低了出错概率。无论是基础查找还是边界查找，开区间写法都能保持逻辑的连贯性，尤其适合在工程实践中推广。
最后，记住二分查找的本质是 “通过缩小区间范围逼近目标”，而开区间正是让这个 “缩小过程” 更清晰、更优雅的最佳选择。下次实现二分查找时，不妨试试开区间写法 —— 你会发现，原来二分查找可以如此简单。