matlab设计滤波器详解
目录
1.filterDesigner 界面介绍
1.1 工具栏介绍
1.2 参数设置介绍
2.设计流程
3.实例
4.参考资料
本文主要记录利用MATLAB的filterDesigner工具设计滤波器的完整步骤,以便后续复用。
1.filterDesigner 界面介绍
1.1 工具栏介绍
滤波器设定面板,如图1所示。
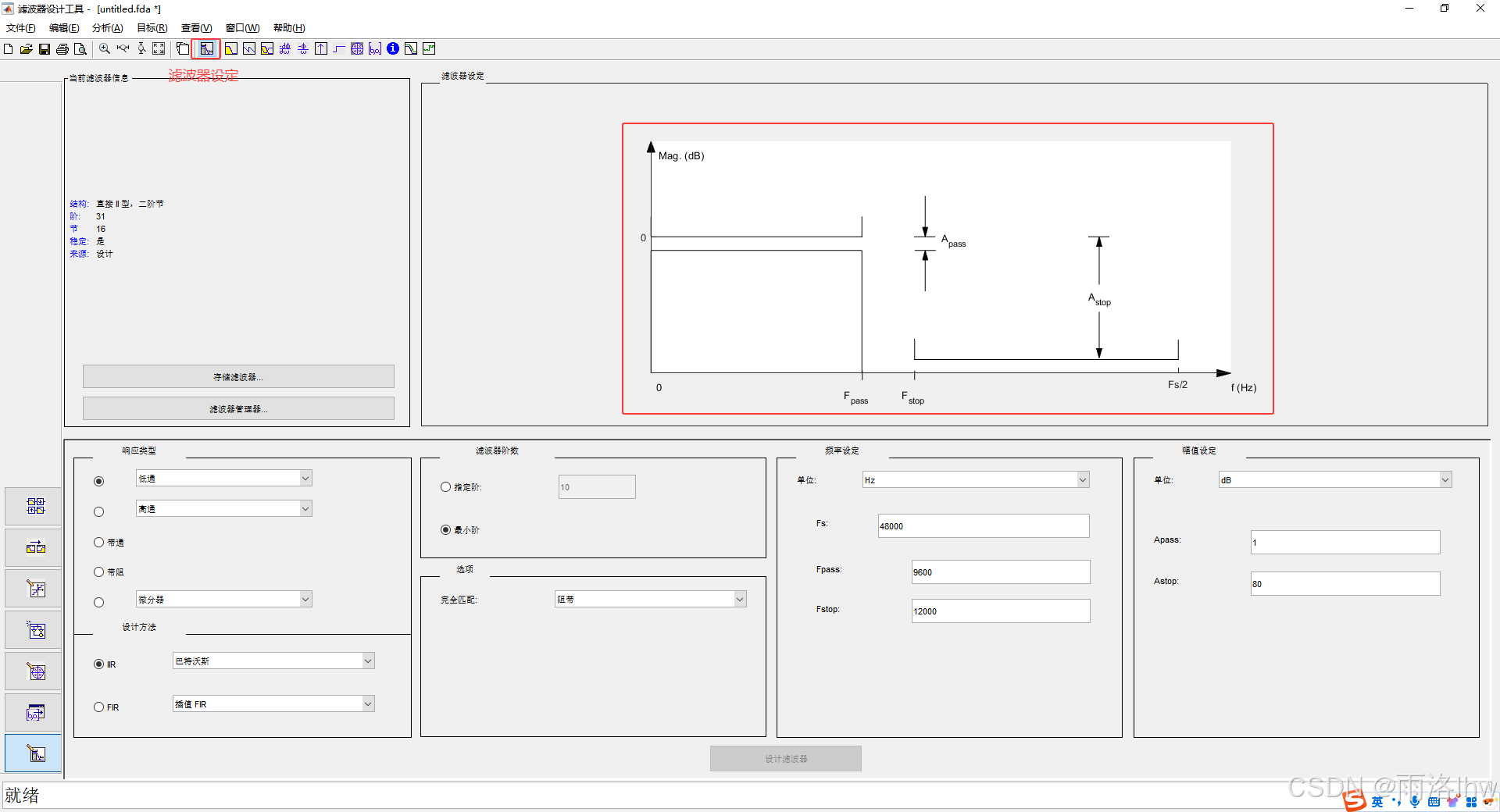
图中可以观察到Fpass(通带截止频率)、Fstop(阻带截止频率)、Apass(通带幅值)、Astop(阻带幅值)、Fs/2(采样频率的一半)的作用。
幅频响应图像如图2所示。
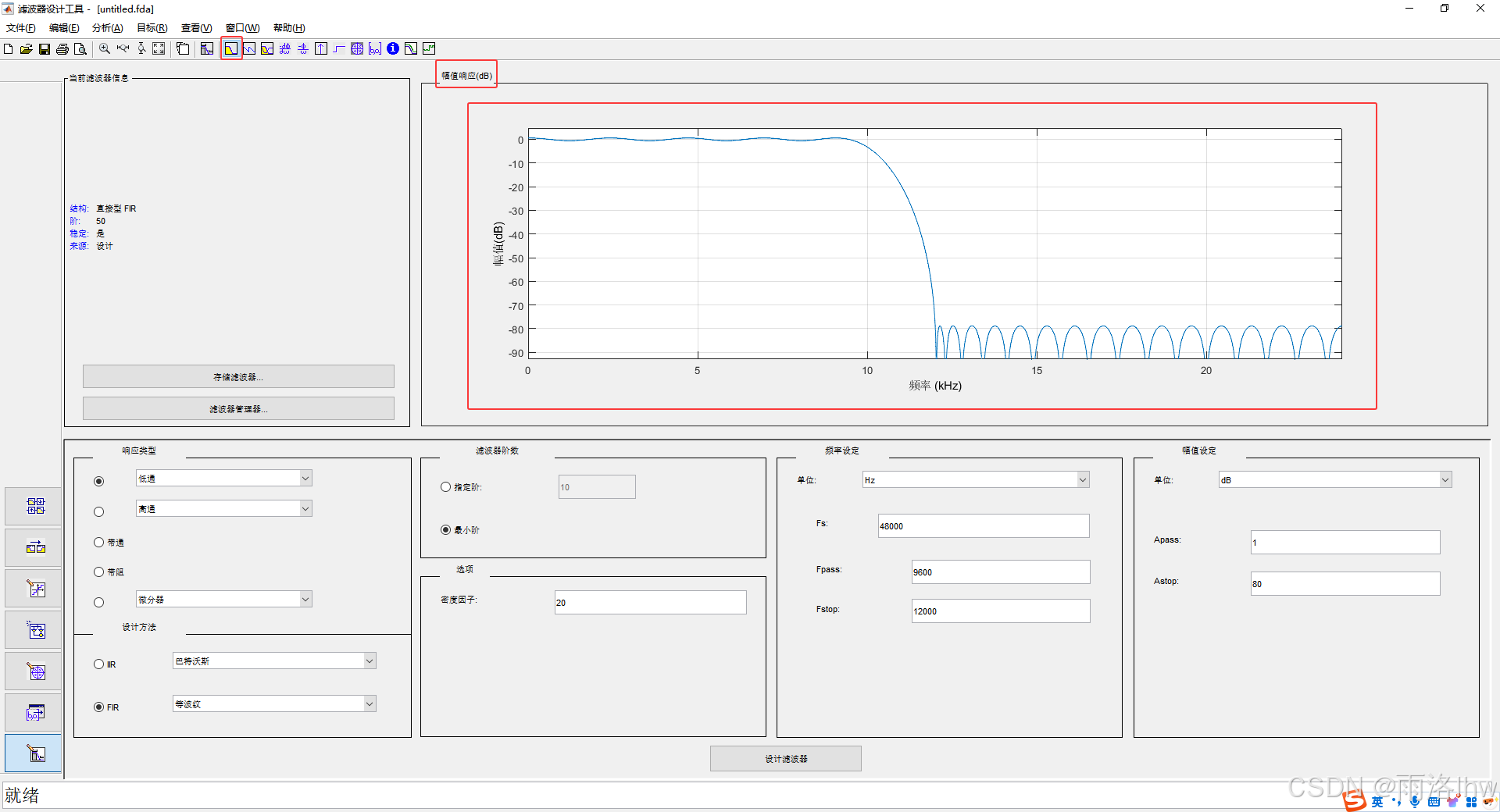
幅频响应曲线能够清晰呈现滤波器的频率特性,便于快速评估其设计合理性和指标符合度。
相频响应图像如图3所示。
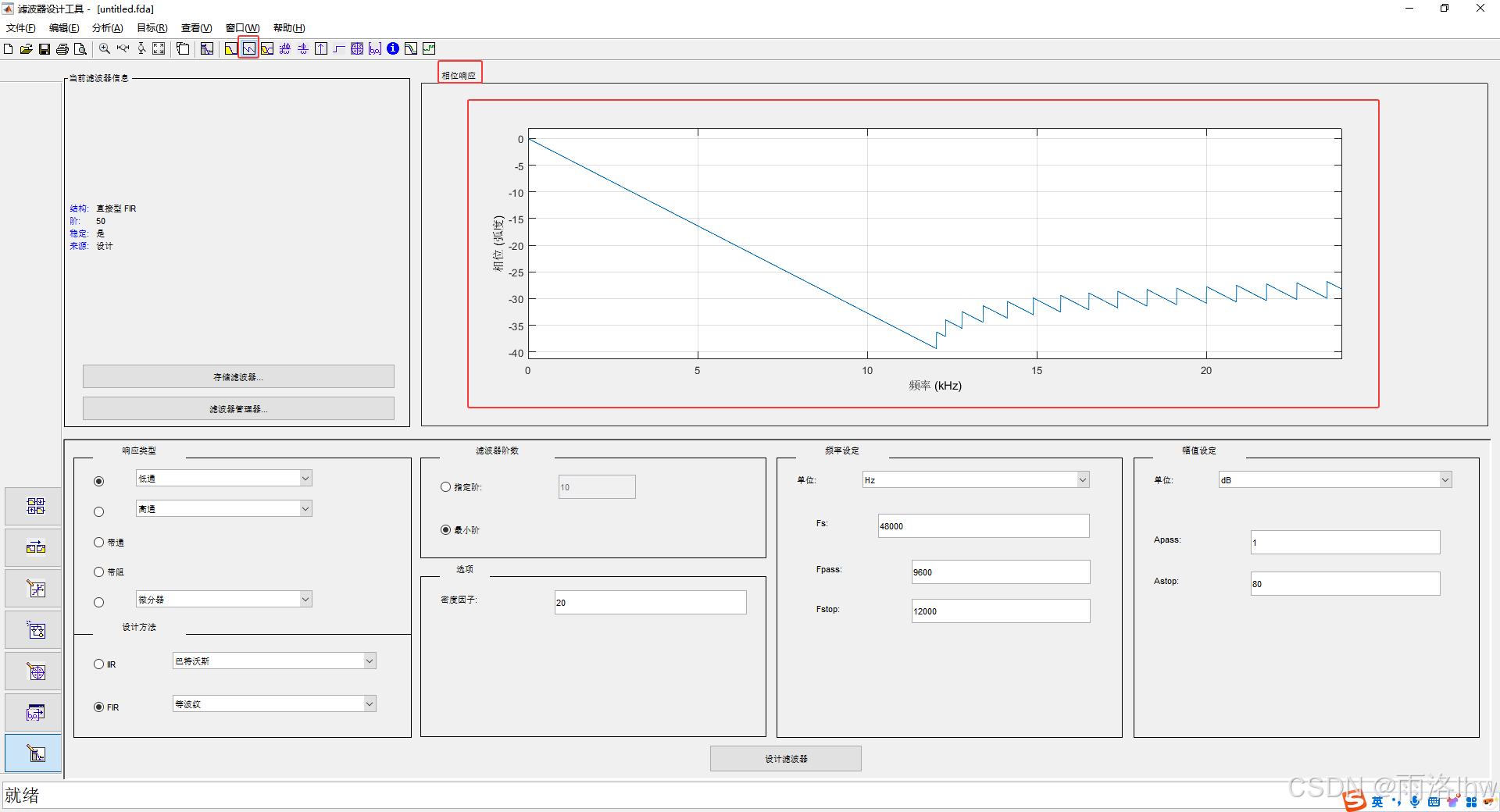
相频响应曲线可以用来判断滤波器是否满足期望的相位特性。
1.2 参数设置介绍
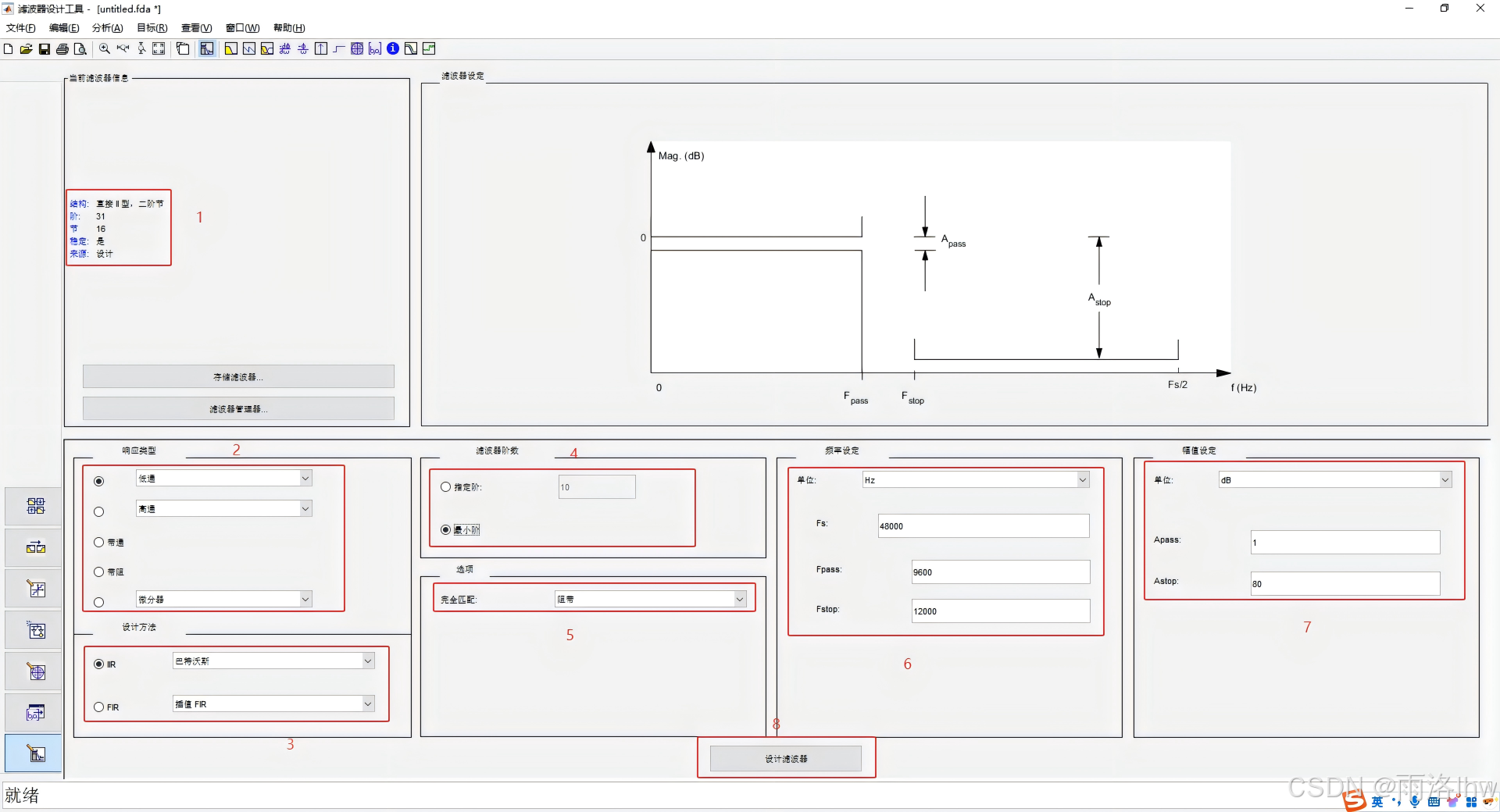
1:滤波器的结构说明,其中包含滤波器的结构,阶数。
阶数:滤波器的阶数等于其传递函数分母的最高次方。阶数越高,滤波器的响应越精细,但计算复杂度也增加。通常,阶数越低,滤波器的实现越简单,但可能无法达到理想的频率响应。
2:滤波器的功能类型,决定其作用的频率范围。除了常见的低通、高通、带通、带阻之外,还有线波滤波器:一种专门设计用于处理线性波形(如信号的方波或脉冲波形)的滤波器,通常用于信号的高精度平滑和特定噪声抑制。它的设计目标是消除特定频率的干扰信号,以保持信号的形状和质量。
3:滤波器的结构类型:FIR(有限冲激响应)和IIR(无限冲激响应)。
FIR滤波器:其输出仅依赖于当前及过去的输入值(无反馈)。单位冲激响应有限,意味着其响应最终会消失。FIR滤波器通常具有线性相位特性,且始终稳定。适用于需要高精度相位控制的场合,但在某些应用中可能需要较高阶数才能达到理想性能。
IIR滤波器:其输出不仅依赖于当前和过去的输入值,还依赖于过去的输出值(有反馈)。IIR滤波器具有无限长的冲激响应,理论上无法完全消失。它们通常具有较低的阶数,但在某些情况下,可能会出现不稳定性。适用于对计算效率有较高要求的场合,但在设计时需要注意稳定性。
4:滤波器的阶数设置
指定阶数:手动设置滤波器的阶数,直接控制滤波器的复杂度和精度。
最小阶数:滤波器的最小阶数是根据给定的通带截止频率(Fpass)和阻带截止频率(Fstop)以及幅值要求(Apass和Astop)自动计算得到的。
5: 选项
完全匹配通带:使通带内的频率响应尽量接近理想值,也就是通过信号的频率范围内,保持信号幅度基本不变。
完全匹配阻带:使阻带内的频率响应尽量接近零,以最大限度地抑制不需要的信号。
6: 频率设定,设定多个频率参数:
Fs(采样频率):滤波器的采样频率,通常用来确定数字信号的处理速率。
Fpass(通带截止频率):通带的截止频率,表示信号开始衰减的频率。在实际应用中,通常设定为Apass幅度下的截止频率。
Fstop(阻带截止频率):阻带的截止频率,表示滤波器开始完全抑制信号的频率,对应幅值是Astop。
7:幅值的设定,单位是dB,Apass表示通带截止频率的幅值,Astop表示阻带截止频率的幅值;
以上就是常用的图像界面和参数设置介绍,接下来介绍一下如何使用。
2.设计流程
用matlab设计滤波器流程如图5所示。

根据需求选择对应功能的滤波器,然后根据设备的算力、是否需要保持线性相位等需求选择FIR还是IIR类型的滤波器,设计完之后将参数保存,等使用的时候拿出来用即可。
3.实例
以低通滤波器为例,采样频率设为100Hz。原始信号由10Hz和40Hz的混合波形组成。滤波器参数设置为:通带截止频率12Hz,阻带截止频率30Hz。
通带截止频率和阻带截止频率一般甲方会有要求,通用的设置规则:
- 通带截止频率一般选择在目标信号的频段内,确保所需信号能够通过滤波器而不被削弱。
- 阻带截止频率必须小于或等于奈奎斯特频率(采样频率的一半)。
- 确保通带和阻带之间有足够的间隔,以便滤波器能够提供良好的过渡和性能。
- 要结合硬件的资源来考虑
滤波器的设置如图6所示。
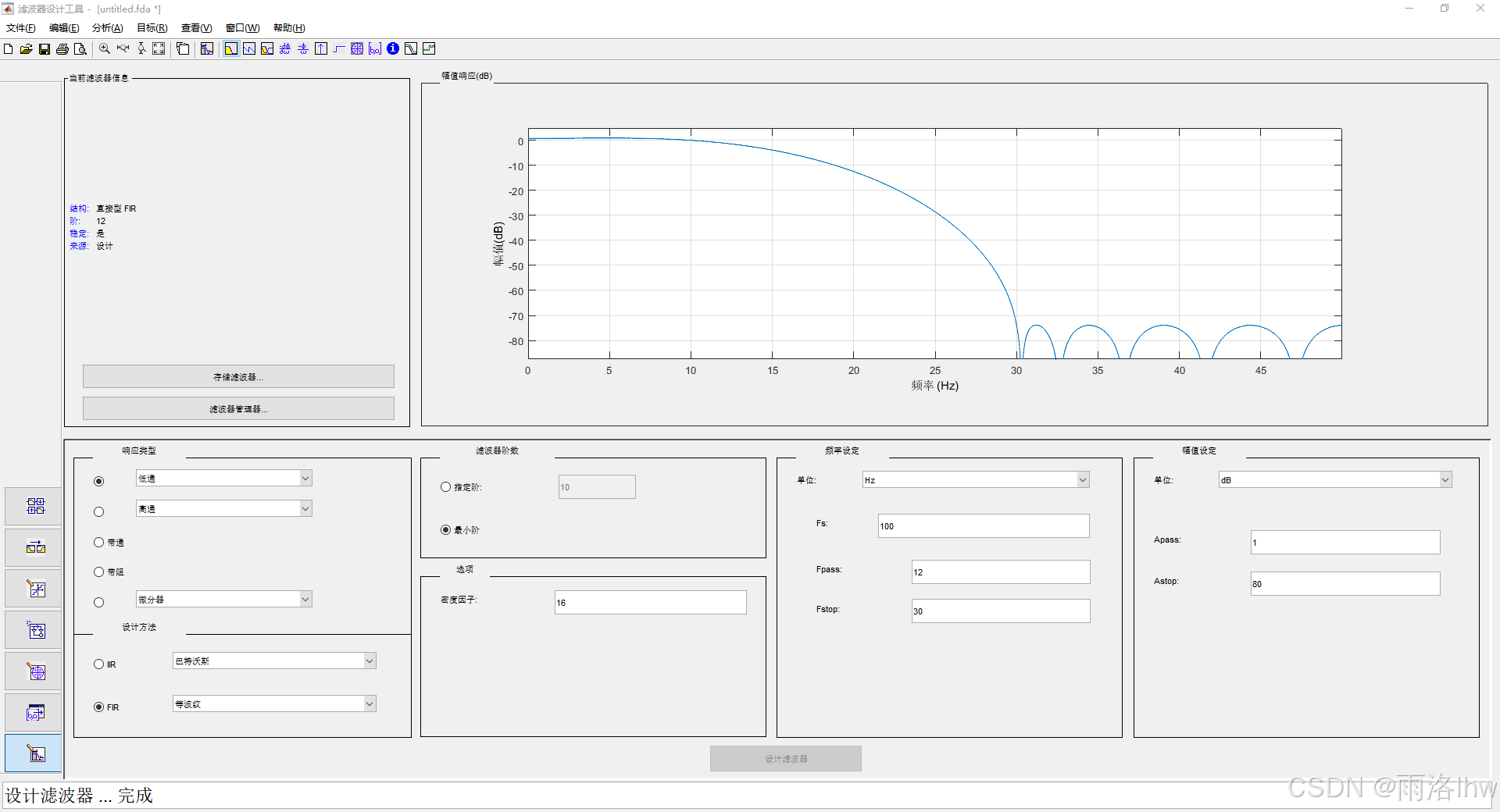
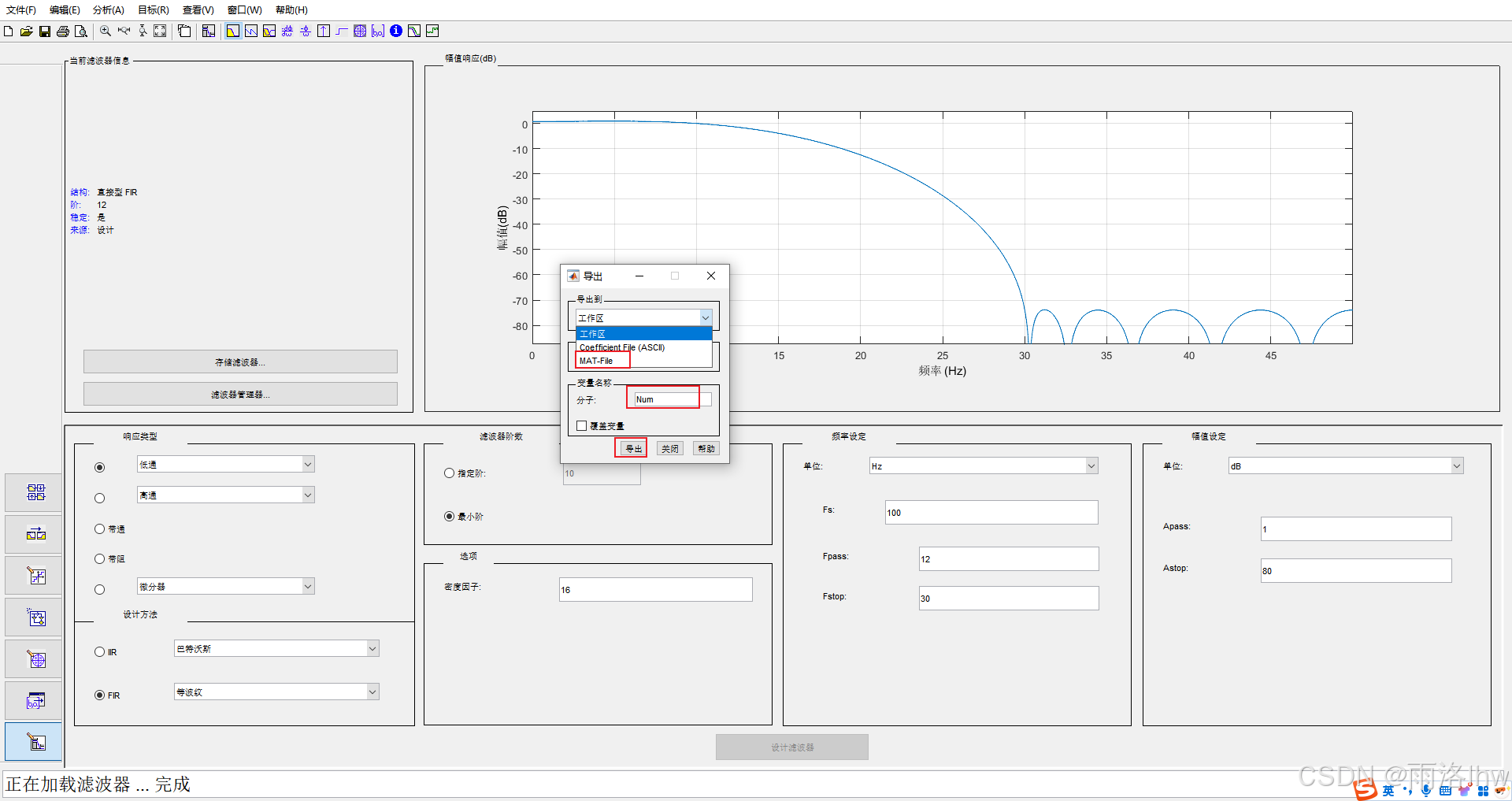
存储滤波器参数:
(1)选择存储滤波器
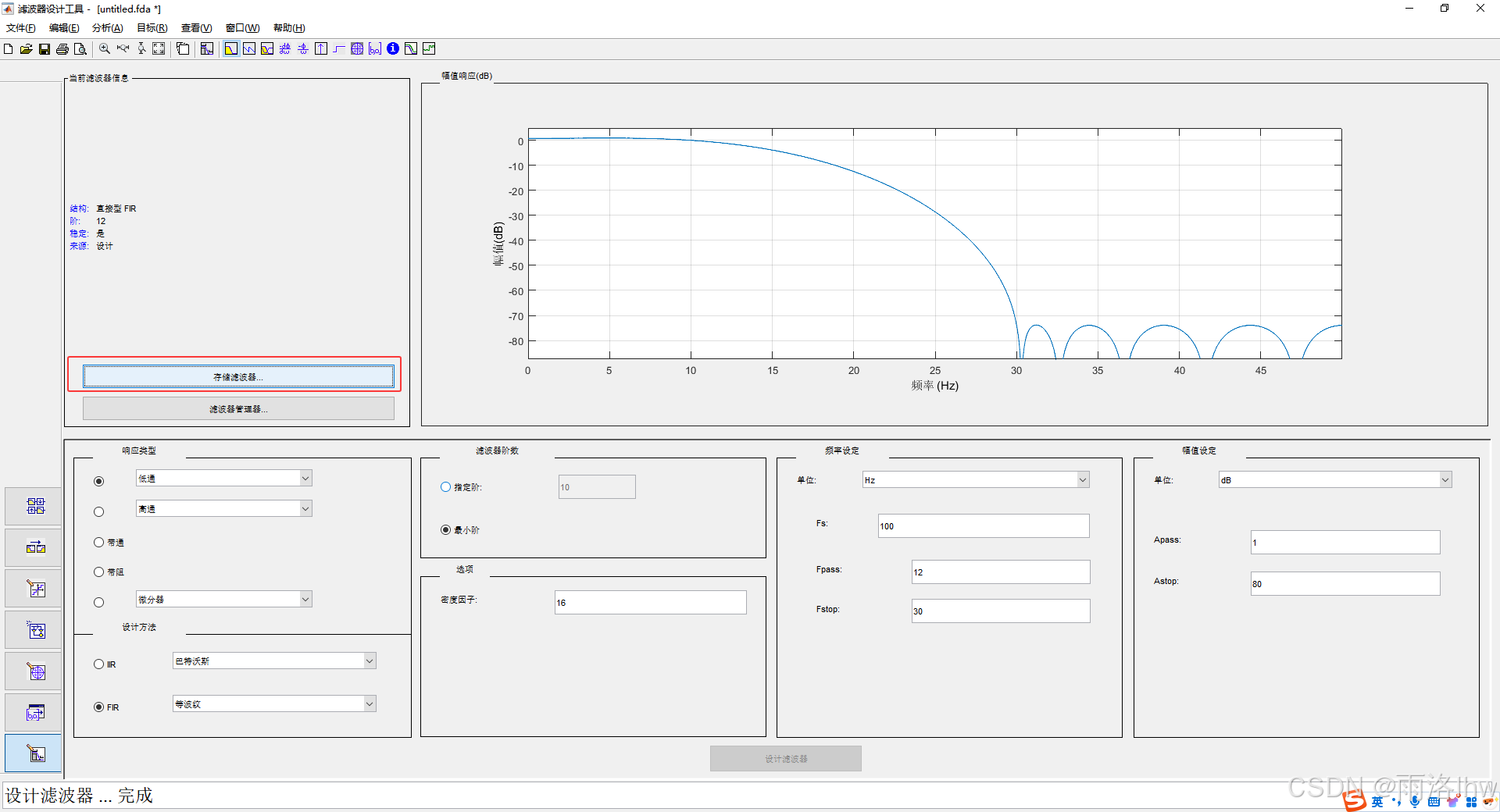
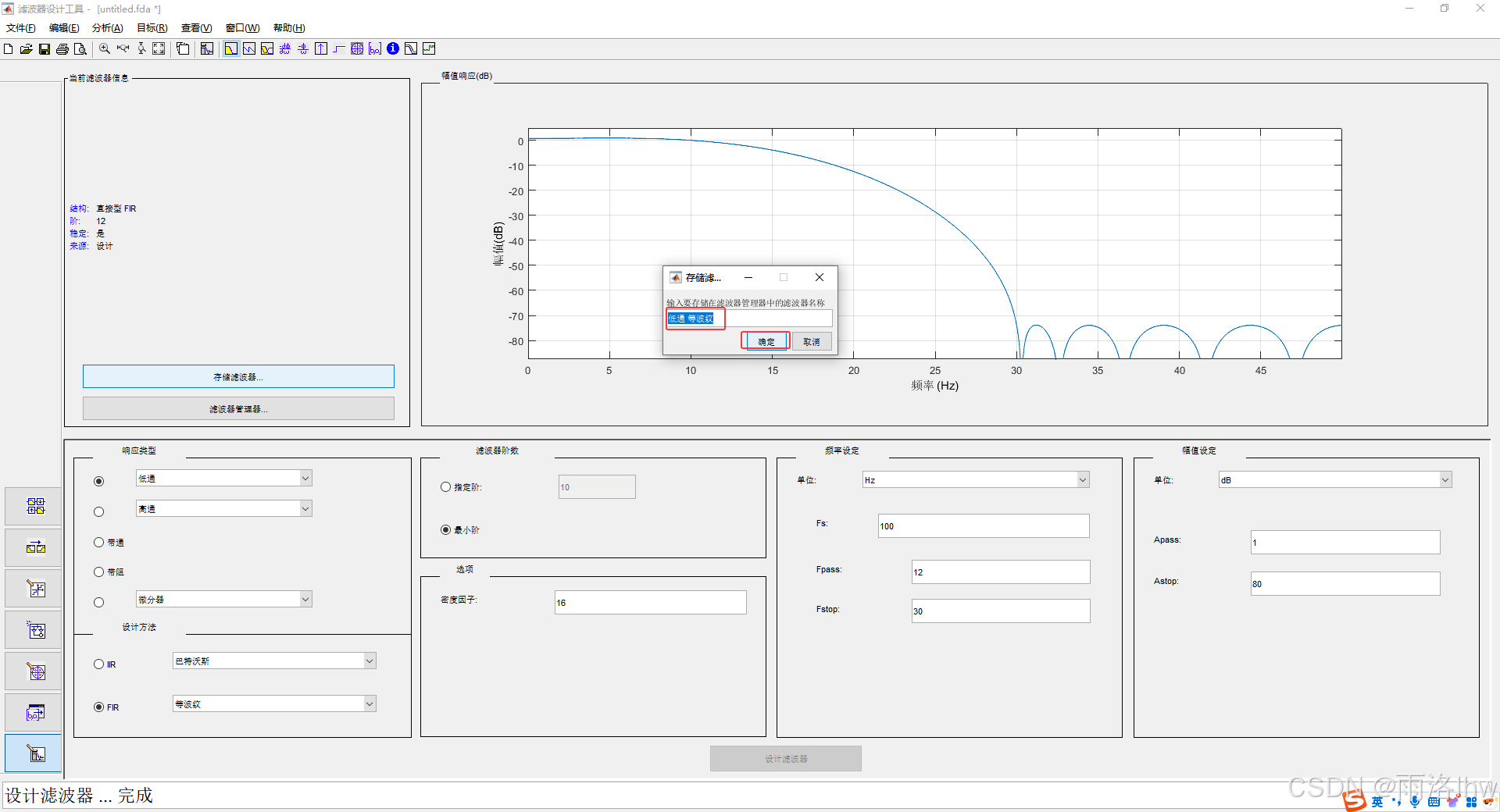
(2)给滤波器命名并点击确定,此时只是将刚刚设置的滤波器保存在filterDesigner中;
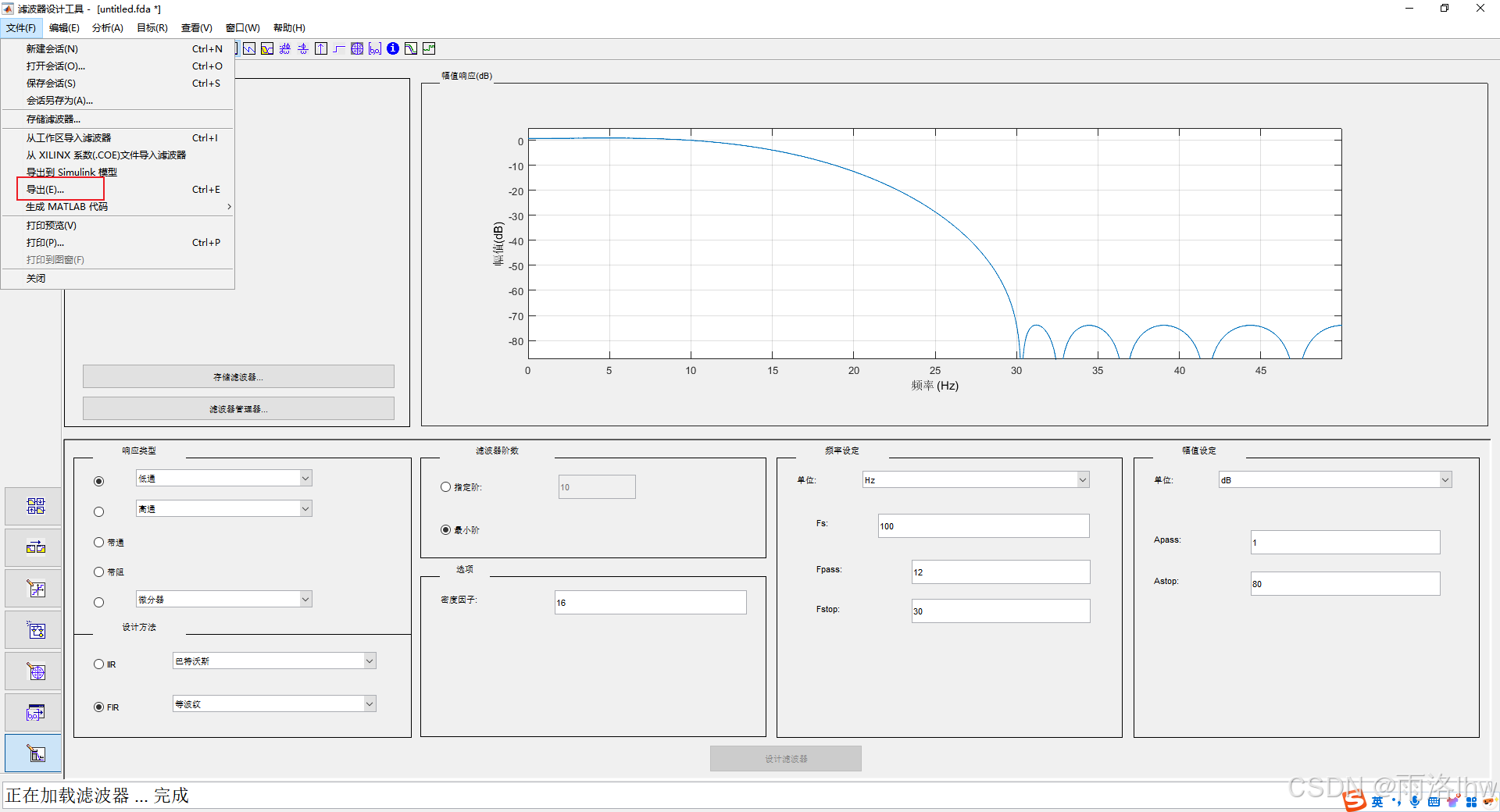
(3)导出滤波器参数;
(4)一般会选择导出为mat文件,然后再导入工作区中,这样方便下次还可以使用这个滤波器,需要注意的是,加载之后调用的变量名必须与保存时一致;
(5)代码使用:
%% 低通滤波器%% 初始设置
% 清空工作空间,关闭无关页面
clc,clear,close all;% 绘图变量
font_size = 12; axis_size = 10; line_width = 2; legend_size = 10.5; marker_size = 12;
figure_width = 14; figure_height = 8; BiaValue = 0;%% //原信号
% //y = 3*sin(2*pi*10*t) + sin(2*pi*40*t);t = 0:0.01:1; %1khz的采样率
y = 3*sin(2*pi*10*t) + sin(2*pi*40*t) ;figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
plot(t, y, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 1])
ylim([-6 6])
set(gca,'XTick',0:0.25:1)
set(gca,'YTick',-6:3:6)
xlabel('时间 (s)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('原信号采样后的波形', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')%% //采样信号频域分析
% 数据长度
datalength = length(y);
% 对数据进行FFT
yFFT = fft(y, datalength);
mag = abs(yFFT);
% 幅值归一化
mag = mag*2/datalength;
pha = angle(yFFT)*180/pi;
% 对无效相位进行置0
for i = 1:datalengthif (mag(1,i)<0.3)pha(1,i) = 0;end
end
% 序列坐标
n = 0:datalength-1;
% 采样频率
fs = 1/0.01;
% 序列频率
f = (0:datalength-1)*fs/datalength;figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(f(1:datalength/2), mag(1:datalength/2), 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 50])
ylim([0 4])
set(gca,'XTick',0:10:50)
set(gca,'YTick',0:1:4)
xlabel('频率 (Hz)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('采样信号的幅度谱', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(f(1:datalength/2), pha(1:datalength/2), 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 50])
ylim([-100 200])
set(gca,'XTick',0:10:50)
set(gca,'YTick',-100:100:200)
xlabel('频率 (Hz)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('相位 (deg)', 'FontSize', font_size, 'FontName', 'KaiTi')
title('采样信号的相位谱', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')%% //滤波器低通滤波
% filtercoe = [0.0282, 0.0188, -0.0095, -0.0477, -0.0527, 0.0122,...
% 0.1386, 0.2661, 0.3197, 0.2661, 0.1386, 0.0122,...
% -0.0527, -0.0477, -0.0095, 0.0188, 0.0282];
load('low_filtercoe.mat');
filtercoe = Num ;
y_Filter = filter(filtercoe, 1, y);% 绘制滤波后的信号
figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
plot(t, y_Filter, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 1])
ylim([-6 6])
set(gca,'XTick',0:0.25:1)
set(gca,'YTick',-6:3:6)
xlabel('时间 (s)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('滤波后的信号', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')%% //滤波信号频域分析
% 数据长度
datalength = length(y_Filter);
% 对数据进行FFT
yFFT = fft(y_Filter, datalength);
mag = abs(yFFT);
% 幅值归一化
mag = mag*2/datalength;
pha = angle(yFFT)*180/pi;
% 对无效相位进行置0
for i = 1:datalengthif (mag(1,i)<0.3)pha(1,i) = 0;end
end
% 序列坐标
n = 0:datalength-1;
% 采样频率
fs = 1/0.01;
% 序列频率
f = (0:datalength-1)*fs/datalength;figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(f(1:datalength/2), mag(1:datalength/2), 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 50])
ylim([0 4])
set(gca,'XTick',0:10:50)
set(gca,'YTick',0:1:4)
xlabel('频率 (Hz)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('滤波后信号的幅度谱', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(f(1:datalength/2), pha(1:datalength/2), 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 50])
ylim([-100 200])
set(gca,'XTick',0:10:50)
set(gca,'YTick',-100:100:200)
xlabel('频率 (Hz)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('相位 (deg)', 'FontSize', font_size, 'FontName', 'KaiTi')
title('滤波后信号的相位谱', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')实验对比结果如下图所示 :
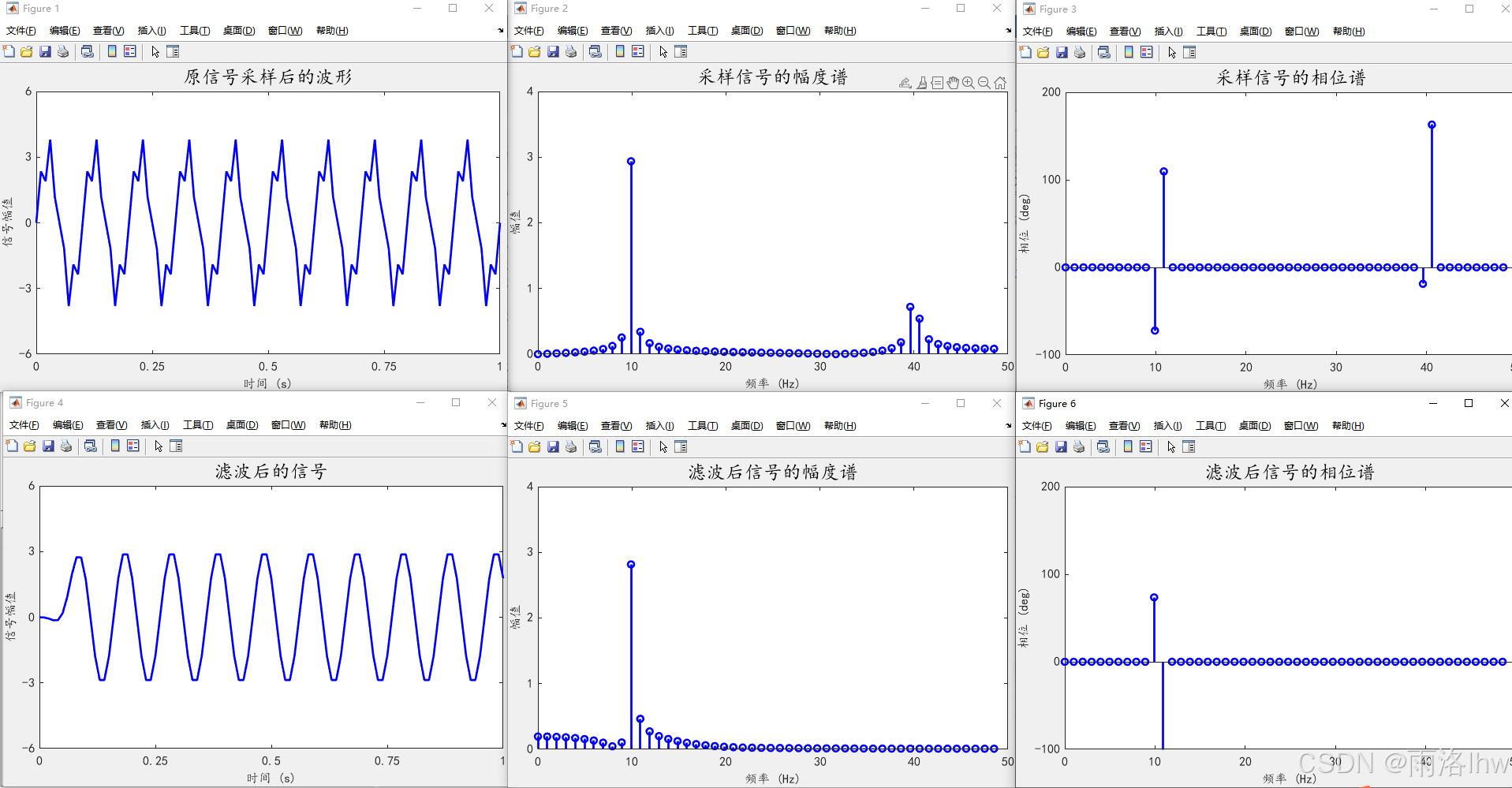
如图所示,经滤波处理后输出信号仅保留了10Hz成分,有效滤除了40Hz干扰。值得注意的是,滤波后的波形整体发生了偏移,这一现象正是FIR滤波器线性相位特性的典型表现。
4.参考资料
1.数字信号处理_第1个Matlab编程实例_哔哩哔哩_bilibili
2.NO.3 深入了解Matlab中的fdatool工具箱_哔哩哔哩_bilibili
以上就是本次笔记的内容,希望对阅读笔记的朋友有所帮助,如果哪里写的不对,欢迎在评论区交流指正。
